Перестановка слагаемых в бесконечных суммах

В прошлый раз я рассказывал, как математики обманывают маленьких детей. Сейчас я покажу, как они обманывают взрослых. То, что вы увидите - это не математика, это обычный трюк иллюзионистов, математический фокус.

В статье «Что не так с перестановкой слагаемых?» приводится пример бесконечной суммы, якобы доказывающий, что итоговая сумма зависит от порядка сложения. Рассмотрим этот пример с более тщательным соблюдением правил записи математических выражений.

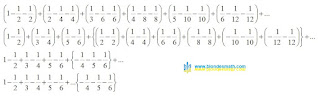Перестановка слагаемых в бесконечных суммах

В первой строке представлена исходная бесконечная сумма, состоящая из шести скобок – по три слагаемых в каждой скобке. Общее количество слагаемых равно 18, итоговая сумма выражения равна нулю. Всё математическое выражение можно разделить на две группы: видимая часть выражения, представленная 18-тью слагаемыми и невидимая часть выражения, состоящая из бесконечного количества скобок, по три слагаемых в каждой скобке. Эти две части разделяет троеточие бесконечности. Обе части равняются нулю.

Во второй строке представлены те же 18 слагаемых после перестановки. Первые три пары слагаемых будут в дальнейшем представлены в видимой части выражения. Фигурными скобками выделена компенсирующая группа слагаемых.

В третьей строке шесть слагаемых видимой части остаются без изменений. Компенсирующая группа, после упрощения выражения, представлена тремя слагаемыми. Итоговый результат после перестановки слагаемых не изменился и по-прежнему равен нулю.

Четвертая строка не имеет к математике отношения. Это обычный фокус иллюзиониста, спрятавшего компенсирующую группу слагаемых в рукав бесконечности (невидимая часть выражения). Цель этого трюка – убедить доверчивых зрителей в «правдивости» ложного утверждения об изменении итоговой суммы после перестановки слагаемых. Да, так поступают карточные шулеры - прячут карту в рукав или достают её оттуда. В цырке подобный трюк называют фокусом иллюзиониста. На юридическом язые это называтся мошенничество.

Можно привести и более грубый пример перестановки слагаемых в данном выражении. Если в видимой части выражения показать слагаемые только с одним знаком, у зрителей неизбежно возникнет вопрос, куда подевались слагаемые с противоположными знаками, а это явно затруднит демонстрацию фокуса.

Перестановку слагаемых в бесконечных суммах наглядно демонстрирует принцип сообщающихся сосудов. Первый сосуд – это видимая часть выражения. Второй сосуд – это невидимая часть выражения, включающая компенсирующую группу слагаемых. Троеточие бесконечности – это соединительный патрубок между сосудами. Итоговая сумма выражения – это общий объем жидкости в двух сосудах. Поскольку в нашем математическом примере итоговая сумма равна нулю, то применительно к сообщающимся сосудам, мы рассматриваем первоначальный общий уровень жидкости в сосудах, как ноль относительной системы координат. Изменение количества или величины слагаемых в видимой части выражения будет приводить к изменению количества или величины слагаемых в компенсирующей группе.

Если последнее выражение рассматривать без невидимой компенсирующей группы слагаемых, тогда это будет не результат перестановки слагаемых, а совсем другая бесконечная сумма, содержащая только часть слагаемых из первоначального выражения и никак с ним не связанная. Доказательством этого факта является разная итоговая сумма двух выражений.

В продолжение начатой темы: "Математические действия с бесконечными рядами".

Перестановка слагаемых

Со школьной скамьи всем нам известно правило, появившееся ещё в древности: от перестановки мест слагаемых сумма не меняется. Об этом матемаики никогда не говорят, но по умолчанию подразумевается, что количество слагаемых и их величина после перестановки остаются неизменными. Если мы изменим количество слагаемых или изменим величину хотя бы одного из них, о перестановке слагаемых уже не может быть речи. В этом случае мы перешли от одной суммы к совершенно другой сумме и эти две суммы никак между собой не связаны.

Но математики утверждают, что после перемены слагаемых сумма может меняться. Даже конкретные "примеры" из жизни приводят. В статье «Что не так с перестановкой слагаемых?», рассчитанной на младших школьников, приводится несколько примеров, якобы доказывающих, что сумма зависит от порядка сложения. При этом матемаики сами не понимают, что же именно они делают. Давайте рассмотрим эти "примеры" более внимательно.

Покупка в ювелирном магазине

Вы приходите в ювелирный магазин. Просите продать вам коробочку для перстня за 100 рублей и перстень за 100 000 рублей. Общая сумма равна 100 100 рублей. Но если вы купите сперва перстень а потом согласитесь на упаковку этого перстня, "то цена покупки может оказаться больше, например 100 тысяч 500 рублей!" (цитирую шедевр математической мысли из оригинала). Что же фактически сделали математики? Они изменили величину одного из слагаемых. Ведь "коробочка для перстня" и "упаковка" - это совершенно разные вещи, если они имеют разную цену. Слагаемое «упаковка», скорее всего, включает в себя: «коробочка_для_перстня + декоративная_коробочка + лента_с_бантиком + пакетик».

Перестановка слагаемых

Покупка на рынке

На рынке продаются апельсины и яблоки по одинаковой цене 100 рублей за килограм. Вы покупаете одно яблоко за 10 рублей и тонну апельсин за 100 000 рублей. Общая сумма равна 100 010 рублей. "Если же вы берете тонну апельсинов, да еще просите добавить туда одно яблоко, «они ведь по одной цене», то получите то же самое, скорее всего, «всего лишь» за 100 000 рублей." (цитирую ещё один шедевр математической мысли). Сумма «яблоко + 1_тонна_апельсин» превращается в другую сумму «1_тонна_апельсин + ноль». Здесь после перестановки одно слагаемое исчезло, что привело к другому результату. Можно предположить, что из тонны взяли один апельсин и заменили его одним яблоком. Либо одно яблоко было подарено бесплатно в качестве бонуса за крупную покупку. Но это уже психология рынка, а не математика.

Вот так взрослые математики обманывают маленьких деток. Но это ещё не всё. Обманывают математики не только маленьких, но и взрослых. Как они это делают? Для этого мы отправимся в цирк и посмотрим на выступление иллюзионистов от математики. Естественно, с разобласением секрета фокуса.