Синус и косинус таблица

Лига лени: Оно вам надо?

Это самая необычная таблица синусов и косинусов. Идея сделать такую таблицу пришла ко мне в процессе написания этих статей:

Почему синус 30 градусов равен одной второй?

Чему равен синус 60 градусов?

Синус и косинус 45 градусов

Я настоятельно рекомендую вам прочитать эти статьи. Тогда вы узнаете, как легко вычислить значения синуса и косинуса самостоятельно. Из этих трех статей я сделал одну таблицу синусов и косинусов.

Синус и косинус таблица

Теперь разбор полетов моей фантазии. Есть много разных способов запомнить значения синуса и косинуса основных углов. Предлагаемый мною способ для тех, кто любит считать. Прежде всего, нужно хорошо запомнить, что косинус - это в сторону, по оси икс. Синус - это вверх, по оси игрек. Дальше изучаем таблицу.

В таблице показано, какие стороны треугольника нужно принять за единицу, чтобы было проще считать. Для 0 и 90 градусов треугольников не существует, это обычные отрезки. Значения синуса и косинуса для этих углов равны либо нулю, либо единице. Всё зависит от положения отрезка - либо вверх, либо в сторону.

Третий столбец таблицы показывает, как использовать теорему Пифагора для вычисления нужного значения синуса или косинуса. Для косинуса 30 градусов и синуса 60 градусов вычисления одинаковы. Для косинуса 45 градусов и синуса 45 градусов вычисление другое. Всё разнообразие таблицы сводится к наглядным картинкам и двум разным вычислениям, которые не трудно запомнить.

Внизу таблицы есть подсказки, как вычислить значения тангенса и котангенса, если вы знаете значения синуса и косинуса. Если вы забыли, как делить одну дробь на другую, воспользуйтесь еще одной подсказкой. Вам нужно умножить первую дробь на обратную вторую дробь.

Синус и косинус 45 градусов

Лига лени: синус 45 градусов равен корень из двух, деленный на два. Картинки смотреть? А зачем?

Наша экспедиция в прошлое помогла нам узнать, почему синус 30 градусов равен одной второй и чему равен синус 60 градусов. Теперь пришло время разобраться с синусом и косинусом 45 градусов.

Если вы были внимательны во время путешествия в прошлое, вы не могли не заметить квадрат, разделенный на две части диагональю. Одна половинка такого квадрата даст нам прямоугольный равнобедренный треугольник. Это очень редкий зверь в стаде треугольников. Математикам он известен уже много тысяч лет и математикам просто скучно возиться с ним.

Прямоугольный равнобедренный треугольник

Да, это уставший треугольник. Он лег на бочок отдыхать. Ну не вечно же равнобедренный треугольник должен стоять на основании, как пирамида Хеопса.

Прямоугольный равнобедренный треугольник

Катеты этого треугольника равны единице (я так хочу). Еще раз повторяю, что оба катета имеют одинаковую длину. Нам неизвестна длина гипотенузы этого треугольника, но мы можем легко вычислить ее по теореме дедушки Пифагора, с которым мы мило беседовали во время нашей экспедиции в прошлое.

Синус и косинус 45 градусов

Как сказал какой-то знахарь математики, синус и косинус угла равны отношению катета к гипотенузе. Поскольку катеты прямоугольного треугольника с углом 45 градусов равны, то значение синуса 45 градусов равно значению косинуса 45 градусов. Берем математику в руки и вычисляем это значение.

Синус и косинус 45 градусов

Почему я умножил числитель и знаменатель дроби на квадратный корень из двух? Маленькие дети не любят комочков в каше. Математики не любят квадратные корни в знаменателях. Очень капризные дяди и тёти.

Чему равен синус 60 градусов?

Лига лени: синус 60 градусов равен корень из трех, деленный на два. Картинки можете не смотреть.

В поисках ответа на вопрос "Почему синус 30 градусов равен одной второй?" мы использовали машину времени. Если кто-то ещё не вылез из этой машины - просьба покинуть аппарат. Больше он нам не понадобится. Теперь мы будем разбирать те материалы, которы были собраны во время экспедиции в прошлое. Сегодня рассмотрим вопрос "Чему равен синус 60 градусов?".

Высота равностороннего треугольника

Берем равносторонний треугольник со стороной, равной единице, и с проведенной через вершину треугольника высотой. Этот рисунок мы рассматривали прошлый раз.

Высота равностороннего треугольника

В этот раз мы не будем поворачивать рисунок, а просто уберем его половину - один из двух прямоугольных треугольников.

Косинус 60 градусов.

Где-то там, в глубине веков, какой-то знахарь математики нам громко кричал про синус и нашептал о косинусе. Шепот гласил, что косинус угла - это отношение прилежащего катета к гипотенузе прямоугольного треугольника. Нас интересует угол в 60 градусов.

Косинус 60 градусов

Прилежащий к углу в 60 градусов катет расположен горизонтально внизу прямоугольного треугольника. Длина этого катета равна одной второй. Гипотенуза этого треугольника равна единице. При делении на единицу число не меняется. Вот и получается, что в этом треугольнике длина прилежащего катета равна косинусу 60 градусов, а значит косинус 60 градусов равен 1/2.

Синус 60 градусов.

Высота этого прямоугольного треугольника будет равна синусу 60 градусов. Как найти высоту прямоугольного треугольника? У нас есть старая добрая теорема Пифагора. Вот её и используем.

Синус 60 градусов

После не сложных вычислений у нас получилось, что синус 60 градусов равен корню квадратному из трех, деленному на два. Прошу заметить, что вычисления для синуса 60 градусов точно такие, как для косинуса 30 градусов. Такова наша математика.

Почему синус 30 градусов равен одной второй?

Лига лени: просто смотрим картинки.

Самый простой ответ на вопрос "Почему синус 30 градусов равен одной второй?" будет звучать следующим образом: так исторически сложилось. Ничего не понятно? Согласен. Нужно глубоко вникать в кучу других интересных вопросов, типа: "Почему прямой угол равен 90 градусов?", "Почему синус мы считаем так, а не иначе?"и так далее. Но есть и другой, более наглядный ответ, если не вникать во всякие "Почему?".

Для этого выбрасываем всякую математическую дрянь из головы, садимся в машину времени и отправляемся на несколько тысяч лет назад, в прошлое. Древний Вавилон. Оказывается, местные аборигены о математике знают гораздо больше, чем о ней помнит среднестатистический наш современник. Корень из двух они легко подглядывают в своей глиняной математической шпаргалке. Какие счастливые люди здесь живут - о тригонометрии ничего не слышали! А это что такое? Так, так, так, учили в школе, знаем.

Равносторонний треугольник

Равносторонний треугольник

Перед нами равносторонний треугольник со стороной, равной единице. Все углы этого треугольника равны 60 градусов. Напомню, что в Древней Месопотамии (а Вавилон располагался именно там) была принята шестидесятеричная система счисления, которую мы с успехом используем сегодня для измерения углов и времени - 60 минут, 60 секунд. Так что для Древней Месопотамии равносторонний треугольник, с его углами в 60 градусов, был очень даже патриотичным.

Мы не станем отправляться в экспедицию по Древней Месопотамии в поисках других местных знаний о треугольниках. Сомневаюсь, что в те древние времена к любопытным чужеземцам относились иначе, чем сейчас. Лучше отправимся в Древнюю Грецию. Уж там точно знали толк в треугольниках.

Высота равностороннего треугольника

Высота равностороннего треугольника

Думаю, что древнегреческие математики уже хорошо знали, что высота равнобедренного треугольника делит его на два одинаковых прямоугольных треугольника. Что высота треугольника всегда перпендикулярна его основанию. Высота разделила угол в 60 градусов в вершине треугольника на два угла по 30 градусов. Основание, равное единице, эта высота так же разделила поровну - 1/2 и 1/2. Очень демократичная дележка треугольника у основателей демократии получилась. И хотя о самих тригонометрических функциях древнегреческие математики ничего не знали, геометрические и вычислительные основы в фундамент тригонометрии они заложили.

Синус 30 градусов

Проходят тысячелетия и тут появляется какой-то знахарь математики и сообщает нам радостную ну такую себе весть: "Я придумал тригонометрические функции!!! Синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе! (Дальше шёпотом) А вот косинус угла равен отношению прилежащего угла к гипотенузе." Упс... И что нам теперь с этим делать? Остается только терпеть и попытаться разобраться во всей этой математической ерунде. Начинаем соображать. Прямоугольный треугольник мы знаем... В углах треугольника мы тоже кое-что понимаем... Вау! Да это же элементарно! Как найти значение синуса для угла 30 градусов? Я просто переворачиваю картинку на 90 градусов и удаляю всё лишнее.

Синус 30 градусов

И так, ещё раз: синус угла - это отношение длины противолежащего катета к длине гипотенузы. В нашем прямоугольном треугольнике длина гипотенузы равна единице. При делении любого числа на единицу, это число не меняется. Следовательно, длина противолежащего катета, равная 1/2, является значением синуса угла в 30 градусов. Как любят говорить математики: "Что и требовалось доказать".

Косинус 30 градусов

Косинус 30 градусов можно легко найти по теореме дедушки Пифагора, ведь треугольник у нас прямоугольный и применять этот математический шедевр мы имеем полное право. Берем в руки математику и считаем.

Косинус 30 градусов

После вычислений у нас получилось, что косинус 30 градусов равен корню квадратному из трех, деленному на два.

Вот как легко всё вычисляется, даже таблицы не нужны.

Линейные угловые функции

Тема занятий:
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В ПРЯМОУГОЛЬНИКЕ
На прошлом уроке мы рассмотрели
Деление

Урок 14

ЛИНЕЙНЫЕ УГЛОВЫЕ ФУНКЦИИ

Если рассматривать конечные тригонометрические функции как координаты точек единичной окружности в декартовой системе координат, тогда линейные угловые функции – это координаты точек хорды, соединяющей точки пересечения окружности с осями координат. Сумма координат любой точки этой хорды всегда равна единице.

Линейные угловые функции

В математике понятия, аналогичные линейным угловым функциям, используются с древних времен – это деление целого на части. В современном мире аналогом являются проценты.

Пояснение для читателей этого сайта. Для себя я называл линейные угловые функции "линос" и "лосес". Как я придумал эти названия? Взял обозначение синуса и косинуса. Визуально они довольно хорошо различаются. В каждом обозначении я заменил первую букву на латинскую букву "l" от слова "line" - линия. Получилось довольно симпатично. Но решать вам. Приживутся ли эти функции в математике и как они будут называться - время покажет. Я просто предлагаю ещё один математический инструмент для описания реальности.

На следующем уроке мы рассмотрим
Сложение

Конечные тригонометрические функции

Тема занятий:
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В ПРЯМОУГОЛЬНИКЕ
На прошлом уроке мы рассмотрели
Три основных типа тригонометрических функций

Урок 4

КОНЕЧНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

Синус и косинус достаточно хорошо изучены, их значения не могут быть больше единицы. Если элементы прямоугольника разделить на длину диагонали, длины сторон примут значения синуса и косинуса. Так же стороны прямоугольника являются проекциями диагонали в перпендикулярных направлениях.

Синус и косинус

Названия всех тригонометрических функций зависят от линии начала измерения угла. Эта же линия определяет направление проецирования. Зависимость между катетами и гипотенузой в прямоугольном треугольнике, известная как «теорема Пифагора» (для единиц измерения длины, не связанных с гипотенузой) или «основное тригонометрическое тождество» (когда за единицу измерения длины принимается длина гипотенузы), является неотъемлемой частью свойств прямоугольника.

Если мы спроецируем единичную диагональ на стороны прямоугольника, то получим две проекции диагонали, выраженные через разные углы. Если мы эти же стороны спроецируем на диагональ, то получим длину диагонали как сумму двух проекций сторон.

Теорема Пифагора

Теорема Пифагора – это зависимость между диагоналями и сторонами прямоугольника.

Тема следующего урока
Бесконечные тригонометрические функции

Синус угла

Рассмотрим отдельные кадры из фильма ужасов под названием "Тригонометрический круг". Поскольку фильм старый, а стереоверсию ещё не пересняли, смотреть мы будем только синусы. Это в стереоверсии на одной картинке будут представлены и синусы, и косинусы, как это обычно показывают на единичной окружности, она же "тригонометрический круг".

Что бы вам там не рассказывали математики, а в общем виде синус в декартовой системе координат - это проекция единичного отрезка на вертикальную ось. Так сказать, тень на стене в лучах заходящего солнца.

Первым у нас будет синус 0 градусов (sin 0) или 0 радиан, кому как больше нравится. Математикам больше нравятся радианы, градусы они терпеть не могут, считают их детской забавой.

sin 0

Синус нуля гардусов равен нулю. Измеряем мы угол в градусах или в радианах - разницы нет. Душещипательную историю о том, как угол появляется на свет и меняет значение синуса, я поведал очень давно на отдельной странице. Почему лежащий отрезок не оставляет тени на стене? Потому, что отрезок не имеет толщины, у него есть только длина. Вот лучи заходящего солнца и скользят беспрепятственно вдоль худенького тельца отрезка.

sin 30

Синус 30 градусов (sin 30), он же синус пи на 6, равен одной второй. Почему синус 30 градусов равен одной второй? Это отдельная история. А пока, наш худенький отрезок приподнялся над горизонтом и на стене сразу же появилась тень. Напоминаю, что солнышко у нас находится справа, там, куда показывает стрелочка с иксом.

sin 45

Значение синуса 45 градусов (sin 45) равно единице, деленной на корень из двух или корню из 2 на 2. Почему так получается? Если мы умножим на корень из 2 числитель и знамель дроби 1 на корень из 2, в результате у нас получится корень из 2, деленный на 2. Зачем так делать? У математиков от корней в знаменателях, наверное, происходит несварение желудка. Они не могут себе позволить раба, таскающего за ними чемоданчик для какашек, как это делает путин. Вот поэтому математики придумали свою СВО - специальную вычислительную операцию. Вот так математики уничтожают квадратные корни в знаменателях и испытывают счастье. Садисты, некторым из них только в путинском гестапо работать. Но продолжим о хорошем, здесь показано почему синус 45 равен корню из 2 на 2.

sin 60

Это был синус 60 градусов (sin 60). Значение синуса 60 равно корню из 3 на 2.

sin 90

Синус 90 градусов (sin 90) равен 1. Здесь он предстает перед нами во всей своей красе, так сказать,в полный единичный рост. Ещё синус 90 градусов называют синус прямого угла, он же синус пи на 2. Больше единицы у синуса значений не бывает, какие бы значения угла математики ни придумали.

sin 120

Синус 120 градусов (sin 120), он же синус два пи на три. Значение у него такое же, как и у синуса шестидесяти градусов. Вы обратили внимание, что солнышко, вместе с отрезком, перелезло через стену и светит теперь с противоположной стороны. Вы считаете, это нормально, что солнышко, как паркурщик, сигает через стену, а ось икс по-прежнему тупо смотрит вправо? Я считаю, что подобная картина никак не отражает окружающую нас реальность, пусть математики хоть лоб себе разобьют об свои учебники. Только вот в жизни математики разбивают наши лбы своими учебниками, если мы чего-то там не понимаем в их шаманских премудростях.

sin 135

sin 150

sin 180

Как-то по-будничному прошли синус 135 градусов (sin 135), синус 150 градусов (sin 150) и вот мы и вернулись к тому, с чего начали - нулевому значению синуса. Только теперь это синус 180 градусов (sin 180), он же синус пи. Наш единичный отрезок оказался с другой стороны от центра системы координат. Или это система координат оказалась с другой стороны отрезка? Как правильно располагать систему координат и отрезок? Это знают только шаманы. Нормальные люди с системами координат особо не заморачиваются - как им удобно, так и располагают. Например, в геодезии ось икс направлена на север.

sin 210

Когда угол становится больше 180 градусов, синус такого угла принимает отрицательные значения. До определенного момента. Как вы видите на картинке, синус 210 градусов (sin 210) равняется минус одной второй. Наверное, мы имеем дело не просто с отрезком, а с зомби-отрезком. Сейчас зомби-отрезок возвращается туда, откуда он появился - в преисподнюю. Там черное-черное солнце отбрасывает белую-белую тень. Но это я так думаю, а шаманы могут объяснять всё совсем иначе.

sin 225

sin 240

sin 270

Дальше, как могилы на российском кладбище, мелькают синус 225 градусов (sin 225), синус 240 градусов (sin 240)... Синусы всё глубже погружаются в ад отрицательных чисел. Когда угол достигает величины 270 градусов, синус опускается на самое дно своего падения. Здесь синус 270 градусов (sin 270), он же синус 3 пи на 2, принимает свое наименьшее значение и равняется -1 (минус единице). Оттолкнувшись от дна преисподней, зомби-отрезок начинает подыматься к поверхности, восставая из ада, черное солнце "русского мира" снова перепрыгивает, уже не через стену, а через окоп на поле битвы положительных и отрицательных значений синуса.

sin 300

sin 315

sin 330

Синус 300 градусов (sin 300), синус 315 градусов (sin 315), синус 330 градусов (sin 330)... В бессильной злобе тает отрицательное значение синуса, как российская армия на полях Украины.

sin 360

Синус 360 градусов (sin 360), он же синус 2 пи. Значение синуса снова равно 0. Отрицательные значения синуса исчезли, как исчезнет путинская россия. Впереди нас ждут положительные значения синуса. Если мы и дальше будем крутить наш отрезок вокруг центра Декартовой системы координат.

Это я вам рассказал свою страшную тригонометрическую сказку. Естественно, шаманы от математики будут вам рассказывать другую сказку. Почему сказку? А вот скоро я вам покажу откуда готовилось нападение то, что математики вам никогда не покажут - тригонометрия в стиле "Жил-был пёс". Но это, если у меня будет вдохновение. А пока у меня есть есть другая история - Легенда о Синусе и Косинусе.

Тригонометрический круг

Более правильным названием этого произведения математического искусства является "единичная окружность", в простонародье больше прижилось название "тригонометрический круг". Вы про платье "в окружность" слышали? Лично я - нет. А про платье "в горошек", оно же "в кружочек"? Наверняка, приходилось слышать. Так вот, круг - это горошек, а окружность - это обручальное кольцо.

Тригонометрический круг

Если бы мне нужно было подобрать символ современного шаманства, то я бы выбрал тригонометрический круг. Почему именно тригонометрический круг? Своей формой он похож на шаманский бубен. Тригонометрический круг разрисован кабалистическими знаками, смысл которых нам могут поведать только шаманы. Свои танцы с бубном шаманы часто исполняют, двигаясь по кругу. По уровню интеллектуального наполнения тригонометрический круг находится где-то между полным идиотизмом и каменным веком. Шаманы с бубнами пляшут свои пляски, Великий Дух Единичной Окружности сообщает шаманам значения тригонометрических функций для определенных углов, шаманы пересказывают эти значения нам.

Если математики будут рассказывать вам, что тригонометрические функции - это координаты точек единичной окружности, не верьте им. Если взять конкретную точку на единичной окружности, то эта точка может принадлежать бесконечному множеству графиков совершенно других функций. Да, если значения тригонометрических функций брать в определенной последовательности и считать их координатами точек в декартовой системе координат, то можно получить окружность с радиусом, равным единице. Но не более того. С таким же успехом в декартовой системе координат можно набросать ваш портрет, но это не будет означать, что ваш портрет - это вы и есть.

Тригонометрический круг показывает значения синусов и косинусов при определенных углах. Для простоты давайте разделим этот круг на составляющие. Сперва уберем с картинки всё, что относится к синусам, и у нас получится тригонометрический круг косинусов.

Тригонометрический круг косинус

Теперь мы уберем с первоначальной картинки всё, что относится к косинусам и получим тригонометрический круг синусов.

Тригонометрический круг синус

Но и это ещё не всё. Те картинки, которые вы здесь видите - это сериал под названием "Значения тригонометрических функций на окружности". Состоит этот сериал из отдельных кадров. Когда учитель математики просит вас показать значение определенной тригонометрической функции для определенного угла, он хочет, чтобы вы выбрали один кадр из всего сериала.

Когда-то, давным-давно, я нарисовал картинки для синусов, но так и не опубликовал их здесь. Наверное, на косинусы сил не хватило и это благородное дело не свершилось. Вот теперь настало время разобрать тригонометрический круг по косточкам на примере значений синуса.

Тригонометрический круг синус и косинус

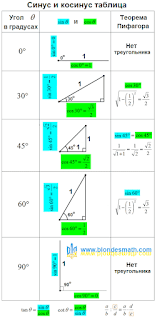
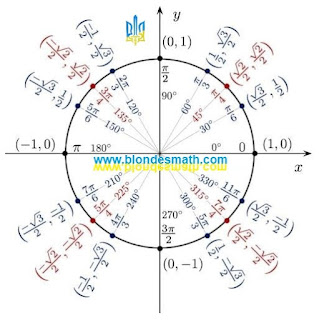
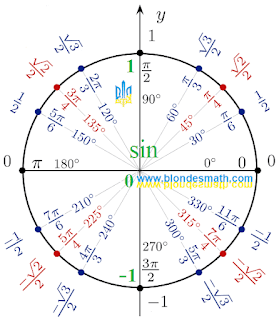
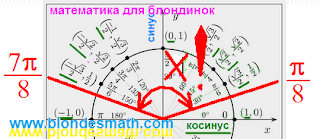
Тригонометрический круг представляет значения тригонометрических функций синус (sin) и косинус (cos) в виде координат точек единичной окружности при различных значениях угла альфа в градусах и радианах.

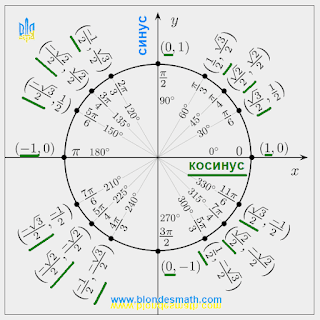Тригонометрический круг синус и косинус

Поскольку я сам вечно путаюсь при переводе координат точек окружности в синусы и косинусы, для простоты все значения косинусов (cos) для углов от 0 до 360 градусов (от 0 пи до 2 пи) подчеркнуты зеленой черточкой. Даже при распечатке этого рисунка тригонометрического круга на черно-белом принтере все значения косинуса будут подчеркнуты, а значения синуса будут без подчеркивания. Если вам интересно, то можете посмотреть отдельные тригонометрические круги для синуса и косинуса.

Напротив указанных углов на окружности расположены точки, а в круглых скобках указаны координаты этих точек. Первой записана координата Х (косинус)

Давайте проведем обзорную экскурсию по этому уголку математического зоопарка. Прежде всего, нужно отметить, что здесь присутствует декартова система координат - одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая - вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы - cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы - sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы - на диване перед телевизором по горизонтали.

В этой системе координат нарисована окружность радиусом, равным единице. Центр окружности находится в начале системы координат - там, где в центе рисунка пересекаются оси абсцисс (ось Х) и ординат (ось У).

Из центра окружности проведены тоненькие черточки, которые показывают углы 30, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 градусов. В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.

Линии углов заканчиваются точками на единичной окружности. Возле каждой точки, в круглых скобках, записаны координаты этой точки. Первой записана координата Х, которая соответствует косинусу угла, образовавшего эту точку. Второй записана координата У этой точки, что соответствует значению синуса угла. По картинке довольно легко находить синус и косинус заданного угла и наоборот, по заданному значению синуса или косинуса, можно легко найти значение угла. Главное, не перепутать синус с косинусом.

Обращаю особое внимание на тот факт, что если вы по значению синуса или косинуса ищите угол, обязательно нужно дописывать период угла. Математики очень трепетно относятся к этому аппендициту тригонометрических функций и при его отсутствии могут влепить двойку за, казалось бы, правильный ответ. Что такое период при нахождении угла по значению тригонометрической функции? Это такая штучка, которая придумана математиками специально для того, чтобы запутываться самим и запутывать других. Особенно блондинок. Но об этом мы поговорим как-нибудь в другой раз.

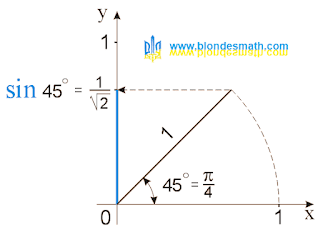
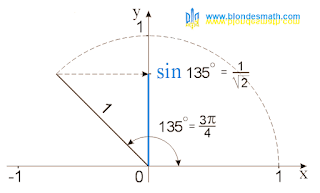
Всё, что собрано в кучку на рисунке тригонометрического круга синуса и косинуса, можно внимательно рассмотреть на отдельных картинках с портретами синуса 0, 30, 45 градусов (ссылки на отдельные странички я буду добавлять по мере увеличения фотогалереи синусов и косинусов).

Найти решение:

Синусы и косинусы круг - здесь картинка во всей своей тригонометрической красе.

Угол 120 градусов в радианах - равен 2/3 пи или 2 пи деленное на 3, на картинке очень красиво нарисовано.

Значения синусов косинусов углов в радианах - на картинке есть такие, надеюсь, именно те углы, которые вы ищете.

Значение косинуса угла в 45 градусов - равно корню из двух деленному на два, можете проверить по рисунку.

Тригонометрическая окружность - я не совсем уверен, что представленная на картинке окружность является тригонометрической, но что-то от тригонометрии в этой окружности определенно есть, например, синусы и косинусы на окружности - вылитая тригонометрия.

Тригонометрический круг рисунок - есть здесь такой. Правда, не самый красивый рисунок, можно нарисовать гораздо красивее и понятнее. Мне минус в репутацию - почему я до сих пор не нарисовал его для блондинок? Представляете ситуацию в картинной галерее будущего: экскурсовод объясняет группе школьников "Перед вами всемирно известное полотно "Тригонометрическая мадонна с единичным отрезком на руках" - картина гениального художника эпохи Раннего Математического Возрождения ..." Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!

Круг синусов и косинусов - именно такой круг совершенно случайно оказался здесь на картинке.

Угол 9 градусов сколько это в пи - в пи это 1/20 или пи/20.
Решение: для перевода градусов в пи радиан, нужно имеющиеся у нас градусы разделить на 180 градусов (это 1 пи радиан). У нас получается 9/180 = 1/20

Ответ: 9 градусов = 1/20 пи.

Синус это вверх или в сторону - синус - это вверх, в сторону - это косинус.

Комментарии к этой статье запрещены. Из-за огромного их количества мои ответы на ваши вопросы о тригонометрическом круге уже не публикуются. Вопросы можете задавать в комментариях к другим страницам. Постараюсь решить проблему за счет удаления части комментариев, тем самым освобожу место для новых.

sin x с минусом

Тут меня заграничные блондинки попросили решить один пример, в котором sin x с минусом. Хоть английского я не знаю, но язык математики в некоторых местах понимать умею. Нужно найти значение икса в пределах от 0 до 360 градусов с градусами, минутами и секундами, если синус икс равен минус 0,8453. В принципе, математика везде одинаковая, по этому и задачи всем задают похожие. Посмотрим, как это выглядит.

sin x = -0,8453

Картинки, с вашего позволения, я использую те же, что рисовал для иностранных блондинок. Так будет быстрее. Прежде всего, определимся с тем, что от нас требуется. Если синус угла равняется какому-то числу, то зная какое-то число, можно найти угол, синус которого будет равняться этому числу ... в доме, который построил Джек! То есть, нужно не по углу искать число, а по числу - угол. Да, буквой икс в математике могут обозначать не только неизвестное число, но и неизвестный угол. Проблема заключается в том, что тригонометрических таблиц с отрицательными значениями синусов и косинусов математики не составляют - суеверия у них такие. При решении подобных задач мы, как и математики, будем пользоваться имеющимися у нас знаниями.

Как математики не обращают внимания на окружающую действительность, так и мы, в начале, не будем обращать внимания на знак минус перед числом. Возьмем тригонометрическую таблицу синусов (она же таблица Брадиса) и найдем в ней число 0,8453. По этому числу мы можем найти угол, синус которого ... в доме, который построил Джек! Этот угол находится в пределах от 0 до 90 градусов и равняется он 54 градуса 42 минуты. Обозначим этот, промежуточный в расчетах, угол через a.

sin x с минусом

На картинке промежуточный угол я обозначил через х вместо a. Вот так выглядит старческий склероз. Кстати, самая лучшая в мире болезнь - ничего не болит и каждый день новости.

sin а = +0.8453

а = 57 градусов 42 минуты

Дальше мы сморим тригонометрический круг и находим угол a. Положительные значения синуса расположены в верхней половине круга, отрицательные - в нижней половине.

sin x с минусом

Одному значению синуса всегда соответствует два значения угла. Найдем эти углы для отрицательного значения синуса a.

sin x с минусом

Первый угол мы получим, если к углу а прибавим 180 градусов. Второй угол получается, если из 360 градусов вычесть угол а.

x1 = 180 градусов + a

x1 = 180 градусов + 57 градусов 42 минуты

x1 = (180 + 57) градусов 42 минуты

x1 = 237 градусов 42 минуты


x2 = 360 градусов - a

x2 = 360 градусов - 57 градусов 42 минуты

x2 = 359 градусов 60 минут - 57 градусов 42 минуты

x2 = (359 - 57) градусов (60 - 42) минуты

x2 = 302 градуса 18 минут

Это было пояснение, как найти sin x с минусом. Теперь это решение нужно записать в соответствии с бюрократическими правилами, которых я не знаю. Выглядит решение приблизительно так.

sin x = -0.8453

x = arcsin (-0.8453)

x1 = 237 градусов 42 минуты

x2 = 302 градуса 17 минут

Надеюсь, теперь всё. Вот!

Решение тригонометрического неравенства

Решение тригонометрического неравенства

Большой проблемой современной молодежи (ой, прям как путин с телевизора вещаю и, естественно, вру) является решение тригонометрического неравенства. Меня до сих пор пронизывает дрожь при виде этого кошмара. Но крик о помощи заставляет меня действовать.

Решение тригонометрического неравенства

Я наберусь храбрости и попытаюсь вступить в смертельную схватку с грозным противником. Выглядит он весьма внушительно - синус 2 икс больше единицы, деленной на корень из 2.

sin2x больше 1/√2

Аркаем выражение - нагло приписываем к обеим частям неравенства неприличное слово "арксинус". По логике, знак не должен изменяться. Арксинус синуса превращается в пшик и у нас остается 2х. Арксинус единицы, деленной на корень из двух превращается из гадкого утенка иррациональных чисел в прекрасного лебедя величиной в 45 градусов. Помогает нам в этом волшебном превращении фея по имени Тригонометрическая таблица.

sin2x больше 1/√2
arcsin(sin2x) больше arcsin(1/√2)
2x больше 45 или
2х больше пи/4

Вот это уже больше похоже на математику. Наши славные 2х теперь больше 45 градусов. А чтобы найти икс, нужно 45 градусов разделить на 2... Хм... Не красиво получается... 22,5 градуса выглядят не эстетично с точки зрения утонченного взгляда математика. Оборачиваемся злым демоном и превращаем прекрасного лебедя величиной в 45 градусов в страшного монстра размеров в пи/4. Если мы разделим этого монстра пополам, то его внешний вид нисколько не пострадает, изменится только циферка в знаменателе: пи/8. При виде такого чуда любой математик расплывется в блаженной улыбке.

2х больше пи/4
х больше пи/8

И так, наши шаманские пляски убедили нас в том, что икс обязан быть больше пи/8. Проведем научный анализ полученного результата. При увеличении икса (угол увеличивается) синус тоже увеличивается. При пи/2 он достигает максимума своей величины и при дальнейшем увеличении возраста, пардон, угла, начинает стареть и дряхлеть, умирая естественной смертью при достижении "пи" - становится равным нулю.

Поскольку наше выражение не может быть меньше указанной величины, в преклонном возрасте необходимо наш икс подпереть костылем в точке пи - пи/8 = 7пи/8 Костыль упираем в спину иксу. В итоге получаем такую картину

7пи/8 больше x больше пи/8

Любой математик при виде такой записи оттопырит губу. Вывернем нашу запись наизнанку

пи/8 меньше x меньше 7пи/8

Математики счастливо улыбаются.

А если мы добавим к своей кабалистической записи навороты в виде периода в 2пи, математики будут визжать от восторга (во всяком случае, меня когда-то так учили). В итоге получаем

пи/8 + 2пи*n меньше x меньше 7пи/8 + 2пи*n

А выглядит наша славная победа вот так.

Решение тригонометрического неравенства

Прямо как крейсер "мос-ква" на дне Черного моря. Большой красный крест на картинке - это не приговор ВСУ российскому флоту, это у меня такая буква икс получилась.

Как запомнить значения тригонометрических функций

При подготовке к экзаменам или ЕГЭ вам может понадобиться вызубрить таблицу значений тригонометрических функций. Возникает вопрос: как запомнить значения тригонометрических функций? Могу вас обрадовать - особо сильно зубрить ничего не нужно. Есть довольно простой, механический способ получить значения тригонометрических функций для самых распространенных углов. Это углы в 0, 30, 45, 60 и 90 градусов. Для других углов математики сами редко что помнят - зачем забивать голову всякой ерундой, когда есть справочники, таблицы и калькуляторы?

Способ очень простой. Берете чистый листик бумаги. На нем записываете числа 0, 1, 2, 3, 4. На эти числа одеваете шапочку квадратного корня. Затем весь этот пионерский отряд в шапочках делите на число 2. У вас получились детские примерчики, которые вам нужно решить. Если вы дожили до тригонометрических функций, то такие примеры вы должны щелкать, как орехи, не прилагая особых умственных усилий. Напоминаю, что корень из нуля равен нулю, корень из единицы равен единице. Чему равны корни из двух и трех ни вы, ни я не помним, поэтому их мы просто оставляем как есть, в шапочках. Корень из четырех равен двум. Теперь всё это добро нужно разделить по-братски - пополам. Делим каждое полученное число на 2. Ноль, деленный на два, равняется нулю. Остальное вы знаете - что не делится, то записываем так, как есть - в виде дроби. В результате этого экзамена по каллиграфии мы получили значения тригонометрической функции синус с дробями и корнями для углов 0, 30, 45, 60 и 90 градусов. Вот видеоролик.



Вот как это выглядит на картинке. Для получения значений косинуса снова решать ничего не нужно. Достаточно перестроить наш пионерский отряд от конца к началу или записать значения углов от 90 градусов до нуля.

Как запомнить значения тригонометрических функций

В англоязычной Википедии этот же процесс подан как половина квадратного корня из тех же чисел 0, 1, 2, 3 и 4. Мы получили значения синуса нуля, тридцати, сорока пяти, шестидесяти и девяноста градусов.

Как запомнить значения тригонометрических функций

Как быть, если вам нужен тангенс одного из этих углов? Очень просто. Решаем ещё один детский пример, в котором значение синуса делим на значение косинуса такого же угла. Или значение косинуса на синус - для котангенса. Напоминаю, что для того, чтобы разделить одну дробь на другую, нужно первую дробь умножить на перевернутую вторую (обратную, в которой числитель и знаменатель меняются местами).

В результате подстановки полученных значений в нужный пример у вас что-то с чем-то должно сократиться. Обычно для этого применяются значения тригонометрических функций с корнями и дробями.

Вот ещё один способ, как запомнить значения тригонометрических функций - математика на пальцах. Эта шпаргалка будет всегда при вас и ни один учитель не сможет её отобрать.

Как запомнить значения тригонометрических функций

Единственный недостаток этого способа - арифметика. С детства нас учили на руке считать пять пальцев, а тут вдруг - четыре! Весь фокус в том, что с детства мы пальцы считаем, начиная с единицы. В случае со значениями тригонометрических функций, пальцы нужно начинать считать с нуля. Вот так один палец и исчезает.

В заключение совсем не лишним будет рассказать вам, как запомнить тригонометрические функции. До этого изобретения я всегда смотрел в справочник по математике, где находится косинус, а где - синус. После изобретения своей полезной картинки, я вообще перестал в справочник заглядывать при решении задач. Мне проще самому вывести все формулы, чем разобраться в том, что там математики в справочнике насочиняли.

Успехов вам на экзаменах!!!

Синус на синус, косинус на косинус

Решаем очередную задачу по тригонометрии. Здесь есть синус на синус и косинус на косинус. Вот только углы разные у одинаковых тригонометрических функций.

cos62*cos28-sin62*sin28

Начнем с анализа ситуации. Если бы подобную задачку на подкинула Природа, думать особо нечего - Природа очень умная, но не хитрая. Поскольку задача находится в учебнике, значит её придумал человек. А люди очень коварные существа, всю жизнь пытаются кого-то перехитрить. Вот и здесь. Углы у нас даны в градусах. Посмотрим на сумму этих углов - они равна 90 градусов. Не спроста всё это. За этим грозным тригонометрическим выражением явно кроется что-то более простое.

Используем заморские знания о преобразовании тригонометрических функций и приведем все наши синусы и косинусы к одному углу, а потом посмотрим, что из этого получилось. Один косинус превращаем в синус, один синус превращаем в косинус. В результате у нас получились тригонометрические функции с одинаковым углом. Здесь не имеет значения, к какому углу мы придем в итоге - к углу в 28 градусов или к углу 62 градуса, результат будет одинаковым.

Синус на синус, косинус на косинус

Вот теперь у нас получилось что-то более понятное. Дальше вспоминаем первый класс - от перестановки сомножителей произведение не меняется. После этого вспоминаем детский садик - если у нас что-то отнять, мы расплачемся, потому что у нас ничего не останется. Как раз наш случай. В математике это "ничего" обозначается цифрой ноль. Вот этот ноль и был спрятан за таким страшным тригонометрическим выражением.

Синус двух арксинусов

Ещё один пример на жонглирование тригонометрическими формулами. На этот раз попался синус двух арксинусов. При выполнении разных трюков на арене математического цирка нужно помнить, что ваши дрессировщики не заставят вас выполнять те трюки, которых вы не знаете. Нужно применять всё то, чему вас уже научили, начиная с первых классов. Вот пример.

Синус двух арксинусов

Синус арксинуса находится очень быстро - отбрасываем буковки и задача решена. В результате должно остаться просто число или математическое выражение, которое превращается в число. Но в данном случае между синусом и арксинусом стоит число, которое не дает нам тупо выбросить названия функций. В тригонометрии есть формулы двойного угла, вот эту формулу для синуса мы и применим.

Как видим, в результате двойка вылезла из синуса и умостилась впереди нашего выражения. Но в математике не бывает всё так просто. Противная двойка вместо себя оставила нам на память сразу две тригонометрические функции - синус и косинус. С синусом теперь никаких проблем нет - он благополучно уничтожается арксинусом. А вот с косинусом проблемы - внутри него появился всё тот же арксинус. Разные названия тригонометрических функций с арком и без говорят о том, что так просто от них не удастся избавиться.

Есть в математике формулы, которые позволяют перегнать математических зверей из клеток с одними названиями в клетки с другими названиями. Вот такой вот математический зоопарк. И нам в принципе не важно, кого куда загонять - косинус в синус или арксинус в арккосинус. Если мы выполним одну из этих операций, мы получим необходимый результат - оба зверя окажутся в одной клетке. Если мы выполним сразу две эти операции, мы снова окажемся в дураках: косинус арксинуса поменяется на синус арккосинуса - оба зверя по-прежнему будут в разных клетках, только других.

Вам эта ситуация ничего не напоминает? Плюс на минус дает минус, минус на минус дает плюс. Мне кажется, очень похоже. И в том и в другом случае главным является результат. Если мы что-то делаем один раз (умножаем на минус или применяем одну из формул), то результат меняется. Если мы что-то делаем два раза (дважды умножаем на минус или применяем сразу две формулы), то результат не меняется. В случае со знаком числа он так и остается неизменным, в случае с названиями тригонометрических функций - они меняются местами. Это уже фокусы математической симметрии. Как видите, математика - это не просто тупое жонглирование числами или формулами, это ещё и математические принципы решения различных математических задач. Если мы сделаем то или это - получим нужный результат. Если мы сделаем и то, и это - ничё не получим, или получим совсем не то, что нам надо. В математике всё очень просто: два раза соври - получится правда. Это касается любых решений любых задач. Один раз вы врёте, когда допускаете ошибку в ходе решения задачи, второй раз вы врёте, когда подгоняете это решение под заранее известный результат. Лично мне кажется, что почти вся современная математика держится именно на этом принципе. Но это так, лирическое отступление.

Косинус мы трогать не будем, пусть отдыхает. Преобразуем арксинус в арккосинус. Для преобразования арксинуса в любую другую арканутую тригонометрическую функцию есть специальные формулы. В нашем примере число больше нуля но меньше единицы. Используем первую формулу для арксинуса.

Формулы преобразования арксинуса

Кстати, при подготовке решения этой задачи я допустил грубую ошибку и использовал формулу преобразования арккосинуса в арксинус, для чего даже предварительно опубликовал формулы преобразования арккосинусов. Но ни переделывать решение задачи, ни врать второй раз мне не пришлось. От неминуемой смерти меня спасла симметрия тригонометрических функций синус и косинус. Интересно, почему при описании свойств тригонометрических функций математики упорно молчат об этой симметрии? Либо они считают всех дураками, не достойными столь высоких математических знаний, либо сами ничего не понимают в тригонометрии. В математике "знать" и "понимать" - это разные вещи. Говорящие попугаи то же могут знать очень много умных слов, но они ничего не понимают в сказанном.

Таким образом, мы добились того, что наш косинус вместе с арккосинусом бесследно исчезают из нашего уравнения. Дальше мы просто гоняем циферки, выполняя простое математические действия с числами. Как видите, ответ можно получить без всякого калькулятора. Можно просто тупо взять калькулятор и посчитать на калькуляторе без всяких формул. Для проверки полученного результата я так и сделал.