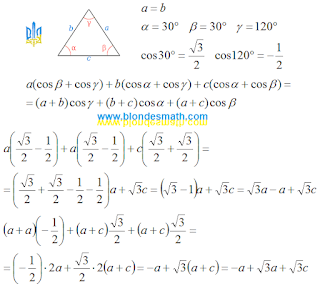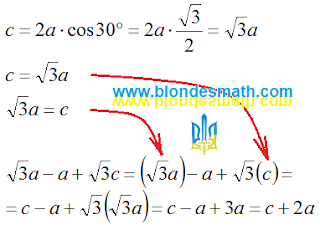Рассмотрим очень простенькую задачу про два угла
треугольника, которые известны. Звучит эта задача так:
Два угла треугольника равны 53 градуса и 57 градусов. Найдите его третий угол треугольника.
У любого треугольника всего три угла. Именно поэтому треугольник так и называется. Величина двух углов из трех нам известна. Теперь я задам вам всего пару вопросов, которые помогут решить эту задачу.
Вопрос первый. Чему равна сумма углов треугольника? Это сакральное знание математики дразнят "Теорема о сумме углов треугольника". Как бы они не называли этот закон природы, суть его не изменится. Кстати, сумма углов треугольника относится к разряду тех математических знаний, которые запоминаются легко и надолго, но которыми вы никогда больше пользоваться не будите в своей повседневной жизни. Бесполезное знание? Нет, но пользуются им люди весьма ограниченного круга профессий, например, геодезисты.
 |
| Сумма углов треугольника |
Вопрос второй. Если вы знаете, что сумма всех углов треугольника равна 180 градусов, с арифметикой сами справитесь? Здесь всё просто. От суммы углов треугольника в 180 градусов отнимаем два известных угла и получаем значение третьего угла треугольника.
180 - 53 - 57 = 70 градусов
Не хотел приводить здесь готовое решение, но... Во-первых, у калькулятора много разных кнопочек и их случайно можно перепутать. В подобных случаях у ученых
исчезают спутники на Марсе, а великая космическая держава рассея свои космические аппараты тупо разбивает об Луну. Так что готовое решение, для контроля, не помешает. Просто проверите себя.
Во-вторых, это очень удобный случай проделать то, что математики настоятельно нам делать не рекомендуют. Нас учат выполнять задания с минимальными затратами времени, и по возможности без записи промежуточных результатов. Собственно, я так и сделал. С одной стороны, это правильно. С другой стороны, это не дает нам возможности понять, а что же мы, собственно, делаем?
Лично мне очень нравится рассматривать решения математических задач под микроскопом в замедленной съемке. Иногда впечатление такое, что наблюдаешь за фокусом в исполнении иллюзиониста и все секреты фокуса тут же вылезают наружу. Давайте рассмотрим подробное решение этой задачи о двух известных углах треугольника и одном неизвестном. Вот как это выглядит.
 |
| Задача про два угла треугольника |
И так. Кто-то измерял углы в каком-то реальном треугольнике. Измерения выполнили только для двух углов. Человек учился в школе и знает, что третий угол можно просто вычислить. Это и есть условие задачи. Теперь подробное решение и описание смысла выполняемых нами действий.
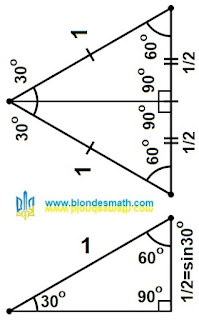
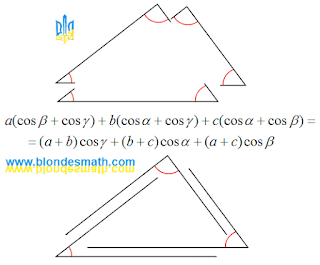
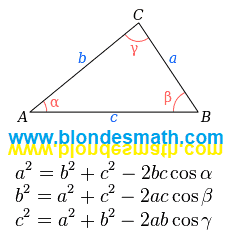
1. Записываем закон, который устанавливает связь между углами треугольника, в алгебраической форме. Я уже говорил, что в математике он называется "Теорема о сумме углов треугольника". Геометрическая форма этого закона представлена на первой картинке.
2. Преобразуем алгебраическую форму закона об углах треугольника под решение нашей конкретной задачи.
3. Вводим в полученную формулу данные из поставленной перед нами задачи. Переходим от алгебраической формы к физической.
4.Анализируем физическую модель решения задачи. Математический аппарат представлен десятичной системой счисления чисел, другие системы счисления отсутствуют. Физический аппарат представлен градусной мерой углов, другие единицы измерения углов отсутствуют. Только при этих условиях мы можем выполнять сложение и вычитание.
5. Переходим к математической модели физической задачи и выполняем математические действия с числами при помощи калькулятора, листа бумаги или в уме.
6. Получаем готовое решение задачи в физической форме.
Вот такой роман почти в стихах у меня получился для одной очень простой задачи. На точность описания сей литературный опус не претендует, поскольку в школе меня такому не учили, выдумывать пришлось на ходу. Все описанные действия мы выполняем автоматически, не вдаваясь в подробные объяснения. Я согласен с математиками в том, что глупо каждое решение задачи расписывать так подробно. Но ещё глупее тупо выполнять те действия, которым тебя учат. В этом случае образование превращается в обычную дрессировку животных.