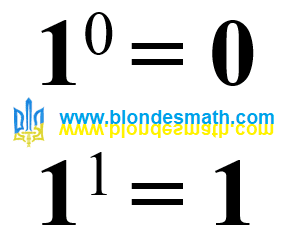Трапеция
На своем англоязычном сайте я однажды уже рассматривал формулу диагоналей трапеции. При переходе от трапеции к прямоугольнику у меня получилось неопределенное выражение – ноль, деленный на ноль под знаком квадратного корня.
Сейчас я предлагаю рассмотреть другую формулу. В 7-м веке индийский математик Бхаскара I вывел формулу для определения с последовательными сторонами a, b, c, d:
 |
| Формула площади трапеции |
Сведения об авторе этой формулы я взял из англоязычной страницы Википедии. Там и раньше была более интересная математика, а уж сегодня... Сегодня вся россия под руководством путина занята тем, что повторяет "подвиг" гитлеровской Германии и им нем до математики.
Прямоугольник
Если к этой формуле применить условия, описывающие прямоугольник, можно получить очень интересный результат деления нуля на ноль:
 |
| Формулы преобразования трапеции в прямоугольник |
Ноль, деленный на ноль, равен нулю. Я категорически против такого результата. Однажды я применял подобный фокус в другой формуле и у меня получилось, что ноль, деленный на ноль, равен единице. С таким результатом я согласен. Но. Никогда никому не верь, даже себе, ты тоже можешь ошибаться. Тут у меня возникла следующая идея.
Результат деления нуля на ноль зависит от математического действия, при котором оно возникает. При умножении результат равен единице, при сложении результат равен нулю.
На будущее нужно будет это запомнить и ничему не удивляться.
Параллелограмм
Вернемся к нашей формуле площади трапеции. Я вспомнил ещё одну геометрическую фигуру, у которой параллельные стороны равны – это .
 |
| Параллелограмм и его площадь |
В этой формуле присутствует синус угла между основанием параллелограмма и его боковой стороной. После преобразования формулы для площади трапеции этот сомножитель вообще отсутствует.
Формула площади параллелограмма легко преобразуется в площадь прямоугольника. Синус угла 90 градусов равен 1. Третий сомножитель в формуле площади параллелограмма исчезает, мы получаем формулу площади прямоугольника.
Деление на ноль
Такой явный баг в формуле площади трапеции говорит о том, что рассматривать результат деления нуля на ноль как правильный категорически не рекомендуется. Формула площади трапеции может применяться только для трапеции и за границами трапеции она не применима. Такая себе «русская математика» только «для внутреннего потребления» трапециями.
После некоторых размышлений, я нашел и второй вариант, подтверждающий мою догадку о результате деления нуля на ноль. Формулу площади трапеции мы преобразовали в формулу площади прямоугольника. После этого формулу площади прямоугольника мы можем без труда преобразовать в формулу площади параллелограмма. Вот как это делается.
 |
| Преобразование площади прямоугольника в площадь параллелограмма |
Вот теперь всё стало на свои места. Снимаю шляпу перед индийским математиком, который учит нас правильно понимать деление на ноль.
Не стесняйтесь проверять математику на прочность. Вы найдете для себя очень много интересного. Математика из сложной науки превратится для вас в обычный инструмент познания.
В заключение могу повторить вывод из предыдущей статьи: хитрые уловки математиков могут привести к ложным результатам. Для примера посмотрите мою статью «Перестановка слагаемых в бесконечных суммах».