Преобразование по иксам

Математическая пародия

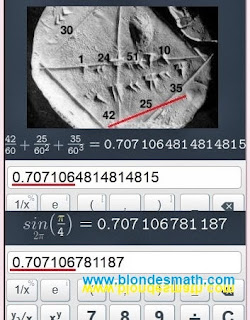
Она сидела за компом вся в расстроенных чувствах. Вконтакте ей уже надоело, в Одноклассниках скучно... Да ещё эта дура патлатая на форуме ей нагрубила...

Взгляд блуждал по комнате... Монитор, глаза бы её его не видели... Стена... Книжная полка... Переплет когда-то любимой книжки... Порывисто встав, она взяла в руки символ своей прошлой жизни, той, в которой книжек было больше, чем Интернета. Из книжки выпала импровизированная закладка - маленький кусочек писчей бумаги...

Ой! А что это за обрывок бумажки у меня тут валяется? Кусочек математики... Хм... Сколько же он уже здесь лежит? Икс с двоечкой в бантике плюс три икса и плюс четверочка...

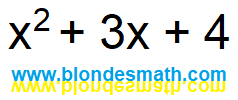Математическое выражение

И что с этим нужно сделать? Нужно решить уравнение. Нееет... В уравнении должен быть "Твикс" - две палочки "равно"... И ещё что-то... А здесь больше ничего нет. Можно это упростить. А где скобки? А нету скобок. Как же без скобок можно упрощать?

Неужели я стала такой дурой, что даже в этой простой задачке разобраться не смогу? Я хорошо знаю математику. В институте я себе одни пятерки по математике покупала...

Вот, правильно. Нужно это как-то преобразовать. А сделать нужно... А сделать нужно... Нужно сделать преобразование по иксам. Берем листик чистой бумаги.... Смотрим, что у нас имеется. А имеется ерунда какая-то. Почему у нас четверка без икса? А потому, что мы его не видим. А когда мы не видим икс? Когда он прячется. И куда же наш икс может спрятаться? А спрятаться он может за единичку.

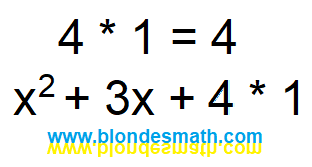Умножение на единицу

А что такое у нас единичка? А это икс в нулевой степени.

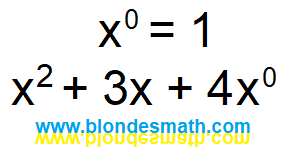Икс в нулевой степени

Что такое икс без бантика? Это икс в первой степени.

Икс в первой степени

А куда подевалась наша циферка перед первым иксом с квадратным бантиком? Ни-ку-да она не девалась, мы её обычно не пишем. Чтобы всё было правильно, нужно эту циферку записать.

Полная запись выражения

Теперь мы можем сложить все циферки сбоку от икса и циферки в бантиках. Вверху циферки можно складывать, я знаю. Вот если все циферки собрать и сложить в одну кучку - тогда будет неправильно. Складывать нужно отдельно, нас так учили. Я помню. Сейчас мы их сложим...

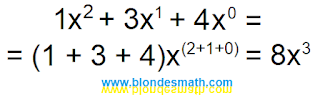Преобразование по иксам

Теперь нужно записать ответ.

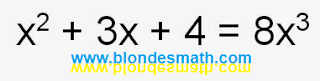Результат преобразования по иксам

Я просто супер! Всё помню. Ага, проверку сделать забыла. Пусть наш икс равняется единице... Прямо как в сказке: "По щучьему ведению, по моему хотению..." превратись-ка ты икс в единичку. Прикольно... Единичка в любой степени равна единичке... Она пофигистка, как Светка... Подставляем и считаем.

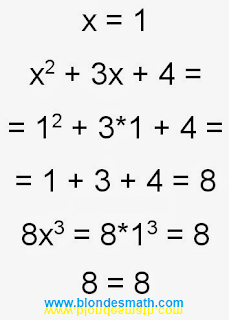Проверка при икс равно единице

Готово. Всё чудненько сходится. Видела бы Ирка, что я умею - умерла бы от зависти. А наша школьная математичка Ирина Павловна говорила, что я ничего не знаю... Я всё знаю и всё умею. Я крутая!

Блин, далась мне эта Ирина Павловна! Она бы сказала, что моя проверка плохая. "На единичку любой дурак умножать умеет!" - слава Богу, она это сказала не мне. Единица ей бы точно не понравилась. Ладно, я возьму двойку. Пересчитываем...

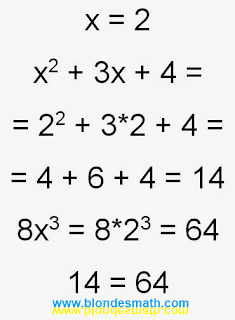Проверка при икс равно два

Упс... Это что за прикол? Я же всё сделала правильно! А почему ответ не сходится? С единичкой сходится, а с двоечкой - ни-фи-га... Я что-то забыла. Забыла дописать... Во второй проверке чего-то не хватает. В первой хватает, во второй - не хватает. И сколько у нас не хватает? Шестьдесят четыре... Отнимаем четырнадцать... Блин, где калькулятор? Ага... Не хватает пятьдесят! И где их взять, эти пятьдесят?

"Вороне Бог послал кусочек сыра..." А что Он нам послал? А нам Он послал пятьдесят. Он всегда посылает ровно столько, сколько нужно. Вот когда для единички не нужно, Он ничего не посылает. А для двоечки... Вау! Я забыла дописать "плюс константа"! Константа - это то, что Бог посылает математикам, когда им чего-то не хватает. А как у нас обозначается константа? А обозначается она у нас буковкой "С". Исправляем ответ...

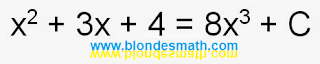Полное преобразование по иксам

Просто супер! Вот теперь это полное преобразование по иксам. Короче, полный пипец. Как хорошо, что мне не нужно больше зубрить эту долбаную математику...

В этот момент где-то в недрах квартиры зазвонил мобильник. Она скомкала два листика бумаги, отнесла их в мусорное ведро и, громко сказав "Да иду я уже! Иду!", не спеша отправилась на поиски своего мобильного телефона.

P.S. Новорожденной идее о преобразованиях по переменной не суждено было стать ещё одним разделом в учебниках по высшей математике. Эта идея отправилась туда, где ей и надлежит быть - в мусор. Девушка и не подозревала, что с любимой игрушкой математиков, переменной, она поступила точно так же, как математики поступают с окружающей действительностью - оторвала числа от содержания и выстроила свою собственную математическую теорию.

Загадка вавилонской таблички

Как хорошо быть дилетантом и ничего не знать. На мир смотришь совершенно иными глазами. Вот из такого моего незнания появилась загадка вавилонской таблички. Лишний раз пришлось убедиться, что когда имеешь дело с математикой, результат может получиться самым неожиданным.

И так, в Википедии я наткнулся на одну интересную картинку, где изображена древняя вавилонская глиняная табличка с изображением квадрата и клинописью. Надпись под табличкой уверяет нас, что здесь приводится значение корня из двух, вычисленное древними вавилонянами почти четыре тысячи лет назад. Вот эта картинка.

Вавилонская табличка корень из двух

Найдена эта табличка была давно и математики провели её исследование. Вот официальная версия, которую я раскопал на просторах Интернета буквально только что. По диагонали представлено значение корня из двух в шестидесятеричной системе счисления. Напоминаю, что составлена она была почти четыре тысячи лет назад. Точность для того времени потрясающая - пять знаков после запятой! Здесь уместно напомнить, что популярные в двадцатом веке нашей эры таблицы Брадиса имели только четыре знака после запятой.

Дальше идет предположение наших математиков, что на табличке изображены три числа. Поскольку нуля и запятой после целой части числа у древних вавилонян не было, то первое число можно трактовать двояко: и как целое число 30, и как дробь 30/60=0,5. Математики предположи, что вавилонская табличка показывает пример вычисления диагонали квадрата со стороной, равной 30. То есть, 30 умножается на корень из двух и получается результат - третье число. Берем в руки калькулятор и проверяем.

Вычисление диагонали квадрата со стороной 30

В принципе, всё логично и вычисления древними математиками выполнены правильно. Но ведь я этого не знал. Я видел только значение квадратного корня из двух и у меня возник естественный вопрос: что означают два других числа?

Предположив, что 42 25 35 - это дробь без целой части, я взял в руки калькулятор и произвел вычисления. Результат показался мне до боли знакомым. Это число пи, деленное на 4? Очень грубое сравнение. Что ещё? Диагональ квадрата связана не только с корнем квадратным, но и с тригонометрическими функциями угла в 45 градусов. Набираю на калькуляторе пи/4, нажимаю кнопочку синуса и... Увиденное меня мня слегка шокировало - синус и косинус угла в 45 градусов представлен с точностью до шести знаков после запятой!

Вавилонская табличка синус и косинус

Вау! Тригонометрические функции в два раза старше, чем принято считать. Два - ноль в пользу древних математиков! Как быть с числом 30? Если это дробь, то читать её следует как 0,5. Я знаю другой класс тригонометрических функций, значение которых для угла 45 градусов равняется 0,5. Получается, что древние математики знали больше нас? Другим классом тригонометрических функций мы пользуемся и сегодня, причем очень широко, но... Мы их называем по-другому, у нас они имеют другие числовые значения и с углами мы их никак не связываем. Оба класса тригонометрических функций можно использовать при решении двух похожих математических задач, которые мы еще не решаем. Или уже не решаем?

Кстати, математика древнего мира мне нравится гораздо больше современной. Я так полагаю, что наших математиков в древнем Вавилоне даже на порог школы не пустили бы. Ответ звучал бы приблизительно так: "Стройте собственные храмы и там проповедуйте свою веру в Определения, Множества и Функции".

И вот, после всех этих размышлений я ознакомился с официальной версией расшифровки вавилонской таблички. Это что - случайное совпадение? Лично я не верю в случайные совпадения. Но и с математикой не поспоришь - оба решения верны.

Какие недостатки у версии с умножением? Почему в качестве первого сомножителя выступает именно число 30, а не любое другое, например, 2? Почему квадратный корень из двух в шестидесятеричной системе счисления представлен с точностью до трех знаков после запятой, а результат вычисления имеет только два знака после запятой? Не хватило места для третьего знака? Не верю.

Какие достоинства у версии с тригонометрическими функциями? Два числа представлены с одинаковой точностью - три знака после запятой. Древняя вавилонская табличка является не примером умножения, а математическим справочником по свойствам квадрата.

Для того, чтобы разгадать загадку вавилонской таблички, нужно проанализировать и другие математические таблички того же периода.

P.S. 04.08.19г. Я не буду настаивать на том, что в древнем Вавилоне были известны понятия синуса и косинуса угла. Значения синуса и косинуса угла в 45 градусов совпадают с числом, равным единице, деленной на корень из двух. Обратные числа били известны в древнем Вавилоне и широко применялись. И так, скорее всего, на табличке, являющейся одним из элементов древнего математического справочника, указаны такие математические сведения для квадрата со стороной, равной единице:

1. Число - корень из двух (длина диагонали).

2. Обратное число - единица, деленная на корень из двух.

3. Число одна вторая (число "30" в шестидесятиричной системе счисления).

Поскольку в древнем Вавилоне вряд ли знали проценты, можно предположить, что третье число на табличке является линейной угловой функцией угла в 45 градусов. Геометрически, линейные угловые функции являются пропорциями деления полупериметра прямоугольника в зависимости от значения угла между его стороной и диагональю.

Были ли известны линейные угловые функции древним вавилонянам? Этот вопрос требует специального изучения, поскольку этот вид тригонометрических функций неизвестен современным математикам. А изучать то, чего не знаешь, очень даже проблематично.

Лично я очень хотел бы посмотреть на подобную справочную табличку древних вавилонян для прямоугольника с углами в 30 и 60 градусов или с другими значениями углов.

Простое построение углов

Тут мне в комментариях задали интересный вопрос. Простое построение углов - как это сделать? Вот сам вопрос.

Вопрос о построении углов

И так, вопрос сводится к следующему - в декартовой системе координат, если брать одинаковый икс и игрек, получим прямую под углом в 45 градусов к осям координат. А как построить углы другой величины? Можно, конечно, заняться гаданием на кофейной гуще и попробовать высчитать, сколько нужно откладывать по иксам, сколько по игрекам, чтобы получился другой удобочитаемый угол. Не 156пи/911, а что-то типа 1, 5, 10, 15 градусов.

Угол в тридцать градусов получается, когда по оси игрек мы возьмем половинку, а расстояние от центра системы координат до точки будет равно единице. При помощи циркуля и линейки такое построить можно, но...

Построение угла в 30 градусов

Для подобного построения необходимо: построить декартову систему координат, нарисовать круг, по оси игрек разделить радиус пополам, через полученную точку провести линию, параллельную заданной... Фокус в том, что о декартовой системе координат древние люди не имели ни малейшего понятия. И ведь тысячелетиями как-то жили, и углы строили.

И так, четвертое-пятое тысячелетие до нашей эры, древняя Месопотамия... Тогда зародилось то, чем мы пользуемся и сегодня. Астрономия, письменность, математика, углы... Какими инструментами тогда пользовались для построения углов? Линейка, циркуль...Возможно, были тогда и угольники, хотя это не принципиально - для построения прямого угла достаточно циркуля и линейки.

Теперь попробуем строить углы при помощи циркуля и линейки без всяких координатных систем. Проводим прямую линию, строим окружность с центром на построенной линии. Ставим циркуль в точки пересечения линии и окружности и строим две окружности того же радиуса. Соединяем линиями центр первой окружности точки пересечения окружностей. У нас получились углы в 60 градусов.

Построение угла в 60 градусов

Почему возле углов я поставил циферки 1, 2, 3, 4, 5, 6? Я считаю, что именно такую единицу измерения углов использовали наши предки. Назовем эту единицу измерения углов "вавилонский угол". Дальше один угол делится на 60 градусов. Почему именно на 60? В те времена, в тех местах, использовалась шестидесятеричная система счисления. Вы такой системой счисления никогда не пользовались и понятия о ней не имеете? Ошибаетесь. Когда вы выражаете время в минутах и секундах, вы используете именно шестидесятеричное счисление. "Подожди пять минут" в переводе на десятичные дроби, если за единицу брать один час, будет звучать как "Подожди 0,083333333... часа". Дико звучит, не правда ли?

Давайте посмотрим на структуру вавилонских шестидесятеричных чисел. Единицу целого числа вавилоняне делили на шестьдесят частей. Потом каждую эту часть делили ещё на шестьдесят частей и так дальше. У шестидесятых долей были свои названия: минута, секунда, терция...

Минута, секунда, терция

Вот теперь я включаю логику и начинаю рассуждать. Если минута - это малая часть, значит могла быть и большая часть или просто часть. Градус как нельзя лучше подходит на роль части вавилонского угла. Тогда первый шестидесятеричный знак после запятой будет называться градус и только второй - минута. Хотя, я могу и ошибаться. Вполне возможно, что градус играет роль целого числа, а придуманный мною "вавилонский угол" - ни что иное, как аналог наших десятков. Но суть не в этом.

Я просто хотел обратить ваше внимание на то, что 360 градусов окружности приблизительно равны 365 дням в году (если отбросить градусы и дни, а тупо сравнивать только числа, как это любят делать наши математики). Почему я сравниваю окружность с днями в году? За сутки Солнце смещается по эклиптике приблизительно на один градус. С другой стороны, вавилонский угол в 60 градусов приблизительно равен одному радиану. Ведь 1 радиан ≈ 57,295779513° ≈ 57° 17′ 44,806″ При этом, у вавилонского угла есть точное числовое значение, а вот радиан точного числового значения не имеет - он построен на бесконечности числа "пи". Один - ноль в пользу древних математиков. Что бы там не утверждали наши математики, но принимать в качестве единицы измерения бесконечное число - это не совсем разумно. Думаю, физики меня поймут - создать точный измерительный прибор для измерения неточной величины даже теоретически невозможно.

Но продолжим наши построения углов. Через центр первой окружности проводим перпендикуляр, затем строим ещё две окружности с центрами в точках пересечения перпендикуляра и первой окружности.

Построение углов 30 градусов

Получился угол в 30 градусов. Как видите, построение очень простое, даже циркуль с переменным радиусом не нужен. Достаточно отрезать кусок разветвления ветки вместо циркуля и всё прекрасно получится. В этой первозданной простоте родились наши современные часы.

Вавилонские углы и циферблат часов

Как видно из рисунка, один час времени равняется тридцати градусам угла. Одна минута времени равна шести градусам угла. В минуте шесть градусов, в окружности шесть углов - что-то в этом есть. Вот только часов на окружности циферблата 12, что не очень вписывается в логику шестидесятеричной системы счисления. У наших математиков везде тупо было бы шестьдесят. В году двенадцать знаков зодиака, в сутках 24 часа. Где-то должна быть очень веская логика именно такого построения временной шкалы. Я не занимался изучением этого вопроса, древние вавилоняне меня и без него шокировали. Но об этом в следующей статье.

Особо стоит отметить, что в древности использовались солнечные часы. Было два варианта солнечных часов - напольные и настенные. Так вот, стрелки этих двух типов часов (тень на циферблате) двигались в противоположных направлениях - по часовой стрелке у напольных и против часовой стрелки у настенных. Можно предположить, что такого понятия, как "вращение по часовой стрелке" у древних математиков не существовало. А в том, что древние люди были очень умными, мы можем убедиться, рассмотрев загадку вавилонской таблички.

Америка

Ученые говорят, что к полному вымиранию динозавров привело падение на Землю астероида размером в 10 километров. Для полного вымирания человечества достаточно одного идиота.

Если вы в этом сомневаетесь, давайте посмотрим на одно недавнее событие сквозь призму математики. Дело в том, что пользоваться математикой нас никто никогда не учил, за исключением решения тех задач, которые перед нами ставят. При анализе событий я использую такие математические штучки, как симметрия, равенство, подобие... Настоятельно не рекомендую применять подобные трюки при общении с окружающими.

Лицам с больным самомнением и слабонервным читать категорически запрещено!

1 октября 2013 года американская государственная система оказалась в состоянии комы. Американский конгресс не принял бюджет. Около 800 000 (восьмисот тысяч) государственных служащих отправлены в отпуск без содержания. И это произошло в стране, претендующей на роль мирового лидера.

Я люблю сравнивать людей с дрессированными обезьянами. Вынужден извинится перед ними - некоторые обезьяны могут посчитать такое сравнение оскорбительным для себя. Ситуация в американской государственной системе гораздо больше напоминает мне поведение тараканов на кухне при включении света. Клац - и никого нет. Вот здесь и начинают появляться очень интересные вопросы, которые обычно задавать не принято.

Почему не принят бюджет США? Что бы там кто не говорил, но суть сводится к тому, что американские конгрессмены не смогли решить вопрос, кто будет воровать из государственного бюджета. Бюджет любого государства - это кормушка для саранчи. Сколько бы денег не выделялось, государственная саранча сожрет всё и заявит, что им мало. Дефицит государственного бюджета - это ситуация, когда аппетиты государственной саранчи превышают возможности налогоплательщиков.

Почему государственные служащие США прекратили работу? Таково законодательство в "самой демократической стране". Очень часто законопослушание сводится к абсурду: одни дураки законы пишут, другие дураки их выполняют. Это преступникам можно не соблюдать законы, законопослушного бунтаря против законодательного идиотизма могут раздавить, как таракана.

Кто ответит за подрыв мировой экономики (напоминаю, США - это лидер на мировом рынке)? Никто. Ведь юридически никакого преступления нет. А давайте сравним последствия законодательного абсурда 1 октября 2013 года с последствиями террористического акта 11 сентября 2001 года.

Атака террористов и атака конгрессменов

В результате атаки террористов погибло около 3 000 человек. В результате междоусобицы конгрессменов никто не погиб. Пока не погиб.

Террористы разрушили здания Всемирного Торгового Центра, повредили здание Пентагона, уничтожили самолеты и так далее. К каким разрушениям приведет отсутствие государственных служащих на своих рабочих местах в государственных учреждениях?

После атаки террористов Министерство обороны США, НАСА, государственные учреждения продолжали свою работу. После атаки конгрессменов прекратили свою работу многие государственные учреждения США. НАСА практически исчезла, даже сайт закрыт. Два американских астронавта оказались в положении дураков, которых забросили на орбиту, а вот вернут ли на землю, это ещё вопрос.

Сайт НАСА не работает

Сколько вертолетов с военными направит президент США в здание Капитолия для "торжества правосудия"? Убить иностранца в собственной спальне без разрешения его правительства - это у американского президента называется правосудием. Я не защищаю террористов. Я просто хочу обратить особое внимание на тот факт, что по отношению к террористам правительство США не соблюдало законы так же, как их не соблюдали террористы по отношению к гражданам США. Как говорится, за что боролись, на то и напоролись. А по отношению к другим преступникам применять подобный принцип - слабо? Возникает весьма интересный вопрос: убить убийцу - это преступление или наказание? Понятно, что все преступники будут требовать соблюдения законов. Но почему законы должны соблюдать только мы, потенциальные жертвы, а не они, преступники?

Корректно или не корректно подобное сравнение - решайте сами. Мы все очень не любим, когда нам в глаза говорят правду.

Можно ли избежать подобной бюджетной ситуации в будущем? Элементарно. Достаточно применить самые простые математические действия. Например, деление.

Пусть все государственные служащие продолжают свою работу, а вот финансирование их работы осуществлять из их собственного кармана конгрессменов. Необходимую сумму делим на всех членов конгресса поровну. Чем дольше они будут копошиться с бюджетом, тем больше денег выложить им придется. Примут ли конгрессмены подобный закон? Никогда в жизни. Ведь это мы дураки, а себя они считают умными.

Можно принимать бюджет по отдельным статьям. Те статьи бюджета, которые уже приняты, принимают силу закона. Вне зависимости от принятия оставшихся статей. Пусть саранча там чего-то и не поделила, но на работе государственного аппарата это никак не отражается.

Можно автоматически считать принятым бюджет прошлого года. Пусть потом законодатели корректируют отдельные статьи, если не смогли вовремя договориться по бюджету текущего года.

Можно в бюджете выделить ряд статей, которые гарантируют бесперебойное функционирование государственных органов, и которые не требуют ежегодного принятия. Они могут только ежегодно корректироваться.

Я не эксперт в законодательстве разных стран, но эти рецепты помогут любой стране избежать американского бюджетного маразма.

В завершение самый интересный вопрос: американские налогоплательщики с 1 октября 2013 года так же дружно не платят налоги, как государственные служащие не выходят на работу? Если продолжают платить, тогда я вообще ничего не понимаю в этом дурдоме по имени "Соединенные Штаты Америки". Кстати, лично я очень сомневаюсь, что в моей стране законодательная ситуация лучше американской.

Математика для взрослых

Если вас не интересует кухня современной науки, дальше можете не читать. Если вам интересно, как решаются некоторые современные задачи - кое-что могу показать. Предупреждаю, это будет математика для взрослых. Дети могут читать в ознакомительных целях, пусть взрослым будет стыдно.

В решении предыдущей задачи есть два момента, которые совсем не бросаются в глаза, но на которые я хотел бы обратить особое внимание.

Момент первый. Я решил не ту задачу, которую меня просили решить, а ту, решение которой я знаю. Свое "бла-бла-бла" на тему "Почему делать нужно именно так, а не иначе" я написал в самом начале, перед решением. Теперь у меня возникает вполне резонный вопрос: сколько задач в современной науке решены именно таким образом? То есть, когда под одну задачу подсовывается решение совершенно другой задачи. Если учесть, что в современной математике вообще никто ничего не понимает, даже сами математики, то такое положение дел лично мне представляется вполне вероятным.

Почему математики ничего не понимают в математике? Да потому, что по определению они оперируют абстрактными понятиями, которых понимать не обязаны. При решении реальных задач абстрактные математические понятия за уши натягиваются на конкретные условия и правильность подобного натягивания никто, кроме математиков, проверить не в состоянии.

Возникает ситуация, которой позавидует любой карточный шулер. За карточным столом любой игрок может быть заподозрен в мошенничестве. Математики - это каста неприкасаемых, в правильности их суждений никто не смеет сомневаться. Либо ты тупо повторяешь то, чему тебя учат математики, либо ты дурак, который ничего не понимает в математике.

В качестве иллюстрации откровенного мошенничества математиков я не стану подвергать допросу с пристрастием одного из их. Я предлагаю открыть одну из страниц Википедии и внимательно прочесть, что там написано. За язык никто никого не тянул.

Умножение

Очень интересная логика у нас. Того, кто занимается подменой за карточным столом, мы называем шулером и считаем преступником. Того, кто занимается подменой вместо поиска математических закономерностей, мы называем математиком и считаем ученым.

А что такое "общепринятое признание"? По сути, это то, что нам внушают математики со школьной скамьи. Если ваше мнение не будет совпадать с "общепринятым", документ об образовании вам никто не даст. Современное образование - это обычная дрессировка обезьян, а не обучение разумных существ.

Как выглядит подмена одного условия задачи другим применительно к дрессированным обезьянам? Обезьяна слышит команду, которой её не обучали. Нормальная обезьяна на такую команду не отреагирует. А жадная? Она выполнит команду, наиболее созвучную прозвучавшей, в надежде получить вознаграждение. Человек - это не только жадная, но и очень хитрая обезьяна. За вознаграждение такая обезьяна не только подмену совершит, но и убить может. Всё зависит от размера вознаграждения.

Второй момент. При проверке решенной задачи я применил одно из свойств треугольника. А теперь давайте проделаем то, что так любят делать математики - в условии задачи вместо одного числа тупо запишем другое. Пусть периметр четырехугольника равен не 23, а 21 дециметр.

После решения задачи с таким условием проверка покажет, что один из треугольников превращается в набор из трех отрезков, которые в принципе не могут образовать треугольник. Сумма двух сторон треугольника равна 7 дециметров, что меньше длины третьей стороны, равной 8 дециметров. Простое изменение числа в условии задачи превращает четырехугольник в рогатый треугольник.

Я понимаю, что сейчас мне математики начнут рассказывать об области определения и области значений... В данном случае я с ними полностью согласен - мы можем проверить результат и пощупать его руками.

А если проверить невозможно? Математики тупо засовывают под знак квадратного корня отрицательное число и утверждают, что в результате получается комплексное число. А где доказательство? Определение? В определении можно написать всё, что угодно. Потом это определение вдалбливается в головы до уровня "общепринятого признания" и "интуитивного понимания" и  уже никакие доказательства никому не нужны.

Лично я не сомневаюсь, что комплексные числа - это такие же рогатые числа, как и рогатый треугольник. Почему при помощи комплексных чисел можно решать определенные задачи? Если знаешь условие задачи и необходимый результат, то подогнать решение большого труда не составит. Тем более, что у математиков всегда есть такое мощное оружие массового оболванивания, как "определение".