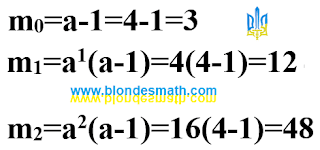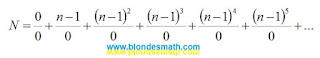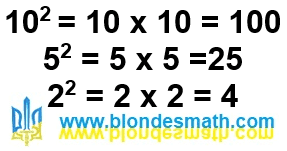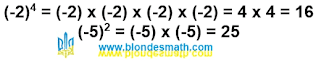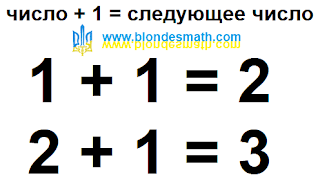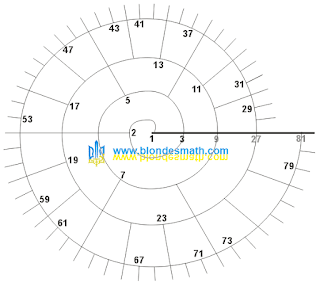
Числовые спирали и простые числа

Числовые спирали и простые числа

https://doi.org/10.5281/zenodo.15024975

Начало: Числовые спирали введение

Все простые числа вида Р находятся в начале числовых лучей на всех числовых спиралях, за исключением простого числа а, расположенного на главной оси а-спирали. Взаимное расположение простых чисел будет меняться в зависимости от числа а, которое лежит в основе построения спирали. Расположение простых чисел на разных числовых спиралях показано на рисунках ниже.

Простые числа на 2-спирали

Простые числа на 3-спирали

Простые числа на 4-спирали

Простые числа на 5-спирали

Составные числа находятся на лучах спиралей, построенных на числах, являющихся делителями этих чисел. На остальных спиралях они расположены в начале числовых лучей. Например, число 6 находится на продолжении 3-луча 2-спирали и является результатом умножения числа 3 на число 2. Это же число 6 находится на продолжении 2-луча 3-спирали и является результатом умножения числа 2 на число 3.

Рассмотрение числовых спиралей будет продолжено в последующих публикациях.

Числовые спирали и системы счисления

Числовые спирали и системы счисления

https://doi.org/10.5281/zenodo.15024975

Начало: Числовые спирали введение

Числа на числовых спиралях могут быть представлены в разных системах счисления. Для примера рассмотрим числа на главной оси некоторых спиралей в разных системах счисления. Таблица 1 показывает числа на главной оси 2-спирали в двоичной, десятичной и шестнадцатеричной системах счисления.

Главная ось 2-спирали

В таблице 2 представлены числа на главной оси 10-спирали в тех же системах счисления.

Главная ось 10-спирали

Аналогично, в таблице 3 представлены числа на главной оси 16-спирали.

Главная ось 16-спирали

Как видно из таблиц выше, каждая а-спираль в системе счисления с основанием а будет состоять из отдельных витков с числами, имеющими одинаковое количество разрядов в позиционной системе счисления. Каждый следующий виток числовой спирали для числа а в системе счисления с основанием а добавляет один разряд в позиционной системе записи чисел. Каждый n-виток состоит из чисел, записываемых при помощи n+1 количества разрядов.

Если ввести правило, что единичные дуги на одном витке должны быть одинаковой длины, тогда числовая спираль превратится в набор концентрических окружностей. Каждая окружность будет содержать числа с одинаковым количеством разрядов. Введение подобного правила нарушает визуальную непрерывность натуральных чисел.

Таким образом, каждая а-спираль является графическим отображением натуральных чисел в системе счисления с основанием а, которая записана в выбранной нами системе счисления. По умолчанию мы применяем десятичную систему счисления.

Продолжение: Числовые спирали и простые числа.

Описание числовых спиралей

Описание числовых спиралей

https://doi.org/10.5281/zenodo.15024975

Начало: Числовые спирали введение

2-спираль

2-спираль

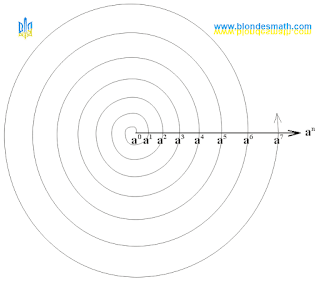
На 2-спирали главная ось образуется последовательными степенями числа 2. Все нечетные числа располагаются в начале числовых N-лучей, все четные числа расположены на N-лучах спирали.

На 2.0-витке находится одна единичная дуга размером 360°, в начале этого витка находится число 1. Это единственная числовая спираль, у которой на нулевом витке нет других чисел, кроме единицы. Количество чисел и единичных дуг определяется по формуле (2).

2.1-виток разбивается на две единичные дуги размером 180° и на нем расположено два числа – 2 и 3. Здесь и на остальных витках количество чисел и единичных дуг определяется по формуле (1).

Вычисления для 2-спирали

2.2-виток образуют четыре единичные дуги размером 90°, на котором располагаются числа 4, 5, 6, 7. Число 6 расположено на продолжении 3-луча.

2.3-виток образуют 8 единичных дуг размером 45°. На этом витке распложены числа с 8 по 15 включительно. Числа 10, 12 и 14 расположены на продолжении 5-луча, 3-луча и 7-луча соответственно.

Дальнейшее расположение натуральных чисел на 2-спирали можно проследить на рисунке выше.

3-спираль

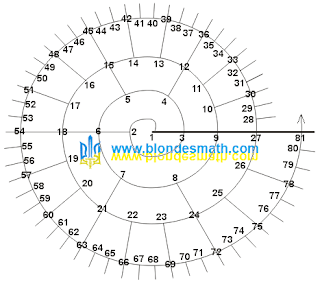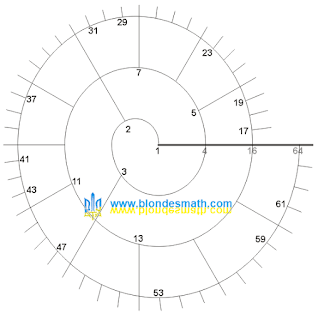
3-спираль

Главную ось 3-спирали образуют последовательные степени числа 3. На 3.0-витке находится две единичные дуги размером 180° и на нем расположено два числа – это 1 и 2. Количество единичных дуг и чисел определяется по формуле (2).

3.1-виток разбивается на шесть единичных дуг размером 60°, на нем располагаются числа 3, 4, 5, 6, 7 и 8. Количество единичных дуг и чисел определяется по формуле (1). Число 6 находится на продолжении 2-луча и является результатом умножения числа 2 на число 3.

Вычисления для 3-спирали

3.2-виток образуют восемнадцать единичных дуг размером 20°, на нем располагаются числа с 9 по 26.

4-спираль

4-спираль

Главную ось 4-спирали образуют последовательные степени числа 4. На 4.0-витке находится три единичные дуги размером 120° и на нем расположено три числа – 1, 2 и 3.

4.1-виток разбивается на двенадцать единичных дуг размером 30°.

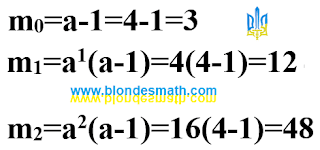Вычисления для 4-спирали

4.2-виток разбивается на сорок восемь единичных дуг размером 7,5°.

Каждый виток 4-спирали содержит в себе два сжатых витка 2-спирали. Сжатие происходит неравномерно и задается структурой нулевого витка 4-спирали. Нулевой и четные витки 2-спирали сжимаются до 1/3 витка 4-спирали, первый и нечетные витки – до 2/3. Такое неравномерное сжатие обеспечивает равенство единичных угловых сегментов всех витков в структуре 4-спирали.

Подобное неравномерное сжатие происходит и на остальных спиралях, построенных на числах, равных степени числа а, больше первой степени. Так, для 8-спирали (а=2³), каждый виток которой содержит три витка 2-спирали, пропорции равны: 1/7, 2/7, 4/7.

5-спираль

5-спираль

Главную ось 5-спирали образуют последовательные степени числа 5. На 5.0-витке находится четыре единичные дуги размером 90° и на нем расположено четыре числа – 1, 2, 3 и 4.

5.1-виток разбивается на двадцать единичных дуг размером 18°.

Вычисления для 5-спирали

5.2-виток разбивается на сто единичных дуг размером 3,6°.

Подобным образом можно построить числовую спираль для любого натурального числа.

Продолжение: Анализ числовых спиралей.

Числовые спирали

Числовые спирали

https://doi.org/10.5281/zenodo.15024975

Начало: Числовые спирали введение

Если для визуального отображения натуральных чисел использовать произвольную спираль и единицы измерения углов, тогда все числа можно упорядочить по следующим правилам:

1. На главной оси а-спирали располагаются числа вида aⁿ в порядке возрастания, где а>1, n≥0.

2. Главная ось совпадает с нулевым лучом единиц измерения углов и имеет следующий вид:

Главная ось числовой спирали

3. Главная ось делит спираль на отдельные витки размером в 360°, которые целесообразно нумеровать по показателю степени числа а, расположенного в начале каждого витка. Например, а.0-виток, а.1-виток, а.n-виток. Расстояние между витками спирали произвольное.

4. Каждый виток а-спирали разбивается лучами на равное количество единичных угловых секторов, которые делят виток на единичные дуги. Каждая единичная дуга имеет произвольную длину и соответствует одной числовой единице. Единичные дуги разделяют два соседних натуральных числа, которые располагаются на пересечениях лучей и витков спирали.

5. Количество единичных секторов и количество натуральных чисел m_n для каждого а.n-витка определяется по формуле (1).

6. Для нулевых витков всех а-спиралей количество единичных секторов и натуральных чисел определяется по формуле (2).

Формулы числовых спиралей

7. Каждая единичная дуга из витка m_n на следующем витке m_n+1 делится на а единичных дуг новыми лучами.

8. В начале каждого луча (N-луч), на пересечении с витком, расположено натуральное число N вида P_a, простое по отношению к числу а.

9. На продолжении N-лучей, в точках пересечения с последующими витками, располагаются натуральные числа, кратные числу а, образующему главную ось а-спирали.

Продолжение: Описание числовых спиралей.

Числовые спирали введение

Числовые спирали

https://doi.org/10.5281/zenodo.15024975

Аннотация

Числовые спирали – это представление натуральных чисел на спирали в единицах измерения углов. Соблюдение определенных правил размещения чисел позволяет получить бесконечную спиральную таблицу умножения для любого натурального числа а>1. Внешний вид и структура конкретной а-спирали будут одинаковыми для любых единиц измерения углов в любых системах счисления натуральных чисел.

Введение

Визуальное изображение натуральных чисел известно давно и имеет вид числового луча.

Числовой луч

Для визуализации чисел на числовом луче используются единицы измерения длины. Числовой луч начинается с нуля, поскольку иначе невозможно изобразить единичный отрезок как единицу измерения. Расстояния между числами одинаковые и равны единичному отрезку.

В 1963 году Станислав Улам предложил изображение натуральных чисел в виде спирали. Сегодня это визуальное представление натуральных чисел известно как скатерть (или спираль) Улама.

Скатерть Улама

Двумерная плоскость разбита на квадраты одинакового размера. В центре спирали находится единица, вокруг неё в каждый квадрат вписывается одно натуральное число по спирали. Данная спираль построена без применения каких-либо единиц измерения, ноль отсутствует.

В 1994 году Роберт Сакс расположил натуральные числа по Архимедовой спирали и получил спираль, известную сегодня как спираль Сакса (в Википедии описана в разделе "Вариации скатерти Улама").

Спираль Сакса

Для построения спирали Сакс использовал единицы измерения углов для поворота и единицы измерения длины для определения расстояния от центра спирали до каждого натурального числа. В центре спирали расположен ноль единиц измерения длины, на нулевом луче единиц измерения углов Сакс расположил квадраты натуральных чисел.

Продолжение: Числовые спирали.

Простое число Х

Простое число X

Илон Маск опубликовал на своей странице в сети "X" опубликовал простое число Х. Это простое число Илона Маска состоит из 1800 цифр. Вы сами в этом можете убедиться, если не забыли таблицу умножения. Количество строк и столбцов (в десятках) обозначено синим цветом на рисунке выше.

Пользователи Reddit затеяли увлекательную дискуссию по поводу этого простого числа. Мне понравились эти комментарии, перевод которых я привожу ниже:

Осторожно: в конце десятого ряда есть хитрая цифра 7.

Совершенно очевидно, что кто-то попробовал несколько настроек, пока не нашел конфигурацию, которая действительно дает простое число. Но да, цифра 7 является наиболее заметной и, конечно же, последним внесенным изменением - по сути, это тот момент, когда автор отказался от более красивого решения :)

Насколько я понимаю, есть специальная программа для рисования цифрами всякого рода бяк в огромных числах. Наверное, есть другая программа для проверки чисел на простоту, типа числа-лузеры, которые даже делителей нормальных не имеют, не говоря про остальное. Вот представьте, вы нарисовали циферками такой гламурненький рисунок в числе. Решили его проверить на простоту, а у этого числа, оказывается, не только куча делителей, а ещё и свой Инстаграм, и кругленький счет в заграничном банке, и целое море других прибамбасов. Как-то так.

Но вернемся к нашему простому числу X. Сейчас я уберу с рисунка все циферки 1 и посмотрим, что осталось.

Простое число X без 1

Как видите, количество восьмерок в линиях не соответствует идеальному шаблону. Ладно верхняя и нижняя части перекладины буквы "Х", где восьмерок в одном ряду 11, в другом 12. Будем считать, что "художник так видит". Но то 5, то 4 восьмерки в разных рядах... Не камильфо. А еще эта цифра 7. Да, даже Илон Маск бессилен против математики.

Меня интересует такой вопрос: сколько денег заплатил Илон Маск математику за эту работу? Лично я не пожалел бы самой большой суммы. Что может быть больше СУММЫ ВСЕХ НАТУРАЛЬНЫХ ЧИСЛ? Ничего. Кому я должен -$1/12? Кстати, почему эту сумму можно использовать в физике, но нельзя использовать для оплаты труда математиков? Вы только представьте, платите математикам самую большую из всех возможных сумм и все проблемы с повышением зарплаты навсегда решены. Вот где волшебная сила математики зарыта. Кстати, это решение российской госдуре очень даже понравится, дарю.

Почему 13?

Нет, сегодня я не буду вам рассказывать, почему число 13 считается несчастливым. Все числа одинаковы. Это мы сами считаем некоторые числа счастливыми или несчастливыми, положительными или отрицательными. Сегодня речь пойдет о сумме двух чисел на циферблате часов. Почему сложение двух цифр на циферблате часов равно 13? Мы видим на циферблате шесть пар таких чисел. Объяснение очень простое.

Почему 13?

Если мы прибавим 1 к одному слагаемому и вычтем 1 из другого слагаемого, сумма останется неизменной. Такой фокус можно повторять много раз и результат сложения не изменится. Это свойство сложения (или свойство чисел?) можно наблюдать не только на циферблате часов, но и на числовой оси.

Сумма на числовой оси

В качестве исходной суммы на числовой прямой можно взять два соседних числа (верхняя картинка) или два числа, расположенных рядом с выбранным нами числом (нижняя картинка). Такие суммы я назвал «суммы разложения». На подобном свойстве чисел можно придумать много разных математических фокусов, типа "загадайте любое число...", а дальше пляски шаманов с бубнами вокруг загаданного числа. Цель - пусть человек сам скажет достаточно информации для отгадывания задуманного числа. Надеюсь, делить на 2 в уме многие научились.

Таблица простых чисел

Простые числа - это натуральные числа, которые делятся только на единицу и сами на себя. Простые числа играют видную роль в теории чисел. Основная теорема арифметики говорит о том, что любое целое число больше единицы либо является простым, либо его можно представить в виде произведения простых чисел. Спорить с содержанием этой теоремы не вижу оснований, а вот к названию лично у меня очень большой вопрос. Если это "основная теорема" арифметики, то у меня закрадываются подозрения, что начало учебника по арифметике наши математики выкурили в виде самокруток ещё в дошкольном возрасте, а в школе начали изучать то, что осталось.

Ниже представлена таблица простых чисел от 2 до 20000. Эта таблица простых чисел может вам пригодиться при сокращении дробей.

Таблица простых чисел от 2 до 1000

Таблица простых чисел от 1000 до 10000

Таблица простых чисел от 10000 до 15000

Таблица простых чисел от 15000 до 20000

Простые числа — любимая игрушка математиков. По состоянию на январь 2019 года самое большое простое число, известное математикам, имело 24 862 048 десятичных цифр. Эта игра с простыми числами настолько увлекательна, что даже я пристрастился к этой игре. Что я могу сказать по этому поводу? Игра в простые числа очень трудоемка и утомительна, но результаты могут быть очень интересными. Я придумал свои правила игры, о которых скоро вам расскажу. Надеюсь, это будет интересно математикам.

Сперва мне понадобились простые числа до 20 000. Я добавил эти таблицы сюда. Потом мне нужны были простые числа до 1 000 000. Потом я плюнул на это грязное дело потому, что мне надоело. Если вам вдруг понадобится, то здесь вы найдете простые числа до 21 000 000.

Каковы результаты моих "научных" изысканий? Ничего интересного, результат оказался всем давно известным - чем дальше в лес, тем больше дров по числовой прямой от нуля, тем реже встречаются простые числа. Разве что на ноль мне удалось взглянуть с неожиданной стороны. Всё красиво оформлю и поделюсь с вами.

Сумма цифр числа

Сумма цифр числа - это пляска шаманов с бубном, которая к математике никакого отношения не имеет. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться нею, но на то они и шаманы, чтобы обучать потомков своим навыкам и премудростям, иначе шаманы просто вымрут.

Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу "Сумма цифр числа". Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры - это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: "Найти сумму графических символов, изображающих любое число". Математики эту задачу решить не могут, а вот шаманы - элементарно.

Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.

1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие.

Графический символ числа

2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные цифры. Разрезание картинки - это не математическое действие.

Разрезание графического символа

3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.

Преобразование цифр в числа

4. Складываем полученные числа. Вот это уже математика.

Сложение чисел

Сумма цифр числа 12345 равна 15. Вот такие вот "курсы кройки и шитья" от шаманов применяют математики. Но это ещё не всё.

С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про странный значок. Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.

Сумма цифр числа

Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты.

Кстати.

Ноль во всех системах счисления выглядит одинаково и суммы цифр не имеет. Это ещё один аргумент в пользу того, что ноль не является числом. Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых - нет. Реальность состоит не только из чисел.

Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой.

Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет.

Как-то так. Если я в чем-то не прав, покажите мне это. Я придерживаюсь правила, которому меня научила математика: никогда никому не верь, даже себе - ты тоже можешь ошибаться.

Позиционная система

Продолжим наш разговор о делении на ноль. Рассмотрим несколько примеров практического применения деления на ноль, без которого мы до сих пор обходились. Как обходились? Вместо алгебраических формул с применением деления на ноль, мы использовали слова. Рассмотрим позиционную систему записи чисел.

Наиболее естественной формой записи числа является одноразрядная система. Для этого бесконечному количеству чисел должно соответствовать бесконечное количество графических символов - цифр. Да, не самый удобный способ записи чисел. Придумать и запомнить такое практически невозможно.

Симметричным решением является унарная система записи чисел. Для изображения бесконечного количества чисел используется только один графический символ. Эта система записи чисел оказалась слишком громоздкой и неудобной в практическом применении.

Как компромиссное решение, наши изобретательные предки придумали позиционную систему записи. Я намеренно не пишу "систему записи чисел", поскольку позиционная система применяется и в грамматике. Смысл графических символов определяется их положением в записи. Так появилась письменность, а вместе с ней позиционная система счисления.

Есть много формул для описания позиционной системы счисления. Но среди них отсутствует одна - формула, описывающая появление разрядов. Я предлагаю делать это с применением деления на ноль. Введение в запись новых разрядов можно записать так:

Позиционная система

Здесь N - это натуральное число, n - основание системы счисления. Ноль, деленный на ноль, описывает сам факт возникновения чисел и соответствует единичному разряду. Заполнив числами единичный разряд, мы придумываем следующий разряд и начинаем заполнять его. Например, десятки, сотни, тысячи... Если формула показывает введение разрядов от меньшего к большим, то при записи чисел мы располагаем разряды в обратном порядке - от больших к меньшим.

Поскольку разряды мы придумываем сами, то и математические свойства они имеют такие, какие мы в них закладываем. Это я к тому, что не стоить путать деление на ноль длины с делением на ноль числа в позиционной системе.

Поскольку практика применения деления на ноль у нас отсутствует, от слова "совсем", не следует считать эту формулу доказательством существования деления на ноль. Это просто способ выражения своих мыслей на языке алгебры. Приживется в математике деление на ноль или нет, посмотрим через пару тысяч лет. Что, вы так долго не живете?! Ну, тогда занимайтесь способами продления жизни, а не разработкой нового оружия для убийства себе подобных.

Разность чисел и предшествующее число

Ещё раз вернемся к теме разности чисел. Задача звучит так: "Записать несколько разностей, в которых вычитаемое - число, предшествующее уменьшаемому". Задача очень простая, если разобраться в тех терминах, которыми пользуются математики.

И так, разность - это вычитание. Когда из одного числа вычитают другое, это обычно называют вычитанием, но иногда используют слово "разность".

Вычитаемое - это число, которое вычитается. Уменьшаемое - это число, из которого вычитают. В записи вычитания на первом месте всегда пишется вычитаемое, на втором месте, после знака минус, пишется вычитаемое. Результат вычитания так же называют разностью чисел.

Теперь разберемся с предшествующими и последующими числами. Возьмем  таблицу натуральных чисел, закроем глаза и ткнем в неё пальцем.

Разность чисел и предшествующее число

Если закрывать не оба глаза, а только один глаз (тот, который видит учитель, если голову правильно повернуть), то можно "совершенно случайно" ткнуть пальцем в то число, которое вам больше нравится. Я попал пальцем в число двенадцать. Так вот, число, на единичку меньше выбранного мною, будет предшествующее. В данном случае, это число 11. Число, на единичку больше выбранного - это последующее. В нашем случае - это число 13.

Когда речь идет о предшествующих и последующих числах, всегда имеют ввиду натуральные или целые числа. О существовании дробных чисел никто не вспоминает, даже если вы о них знаете. Вероятно, понятия предшествующих и последующих чисел появились ещё тогда, когда сами математики ничего не подозревали о существовании дробных чисел. Кстати, очень похожими являются понятия "вчера" и "завтра". Если подставить вместо "сегодня" дату, тогда "вчера" - это предшествующая дата, а "завтра" - это последующая дата. По аналогии со временем можно сказать, что предшествующее число - это вчерашнее, а последующее число - это завтрашнее.

Теперь перейдем непосредственно к решению задачи. Берем любое натуральное число. Записываем это число, ставим знак минус, записываем число, на единичку меньше взятого нами натурального числа, ставим знак равенства и пишем единичку. Какое бы натуральное число вы не взяли, разность между этим числом и предыдущим всегда будет равна единице.

12 - 11 = 1
2 - 1 = 1
159 - 158 = 1
1000000 - 999999 = 1

Теперь мы можем легко ответить на вопрос: как понять предшествующее числу 1000000? Понять очень просто: число, предшествующее миллиону, на единичку меньше самого миллиона - это девятьсот девяносто девять тысяч девятьсот девяносто девять. Берем в руки математику и проверяем.

1000000 - 1 = 999999

Рассмотрим ещё одну задачу, очень похожую на предшествующую. Заметьте, сейчас мы рассматриваем вторую задачу, а предшествующая была первой. Вторая задача звучит так: "Составь и запиши разности, в которых вычитаемое одно из чисел 3, 4, 5, а уменьшаемое число предшествующее вычитаемому".

Если в предыдущей задаче первым стояло большее число, а меньшее (предшествующее) из него вычиталось, то здесь на первом месте нужно писать меньшее (предшествующее) число и вычитать из него большее. В результате мы всегда будем получать минус единицу.

2 - 3 = -1
3 - 4 = -1
4 - 5 = -1

На этом завершим наш маленький экскурс в разность чисел и предшествующее число.

Таблица квадратов натуральных чисел

Таблица квадратов натуральных чисел от 1 до 100

В таблице квадратов натуральных чисел представлены квадраты чисел от 1 до 100. Показатель степени числа в виде двоечки записан справа вверху того числа, которое возводится в степень. Ну, типа число-малыш залезло на плечи взрослому числу и свесило ножки. Для того, чтобы возвести в квадрат (во вторую степень) любое число, его нужно умножить на точно такое же число и записать результат.

Например, десять во второй степени равняется сто, потому что если десять умножить на десять, у нас получится сто. Пять в квадрате равняется двадцать пять, так как все знают, что пять у пять "опять двадцать пять". А вот двойка в квадрате это не что иное, как "дважды два четыре".

Квадраты чисел

Зачем математики такое придумали - степень числа? Для краткости записи математических выражений, чтобы не повторять несколько раз умножение одинаковых чисел. Если при возведении числа во вторую степень мы экономим совсем мало места, то при возведении чисел в большие степени экономия места получается довольно значительная. Наша лень - главный двигатель прогресса.

Степень числа и умножение

Особенностью квадратов чисел, как и всех остальных четных степеней числа, является то, что после возведения в степень отрицательного числа (в математике такое число уже не считается натуральным, его называют целым числом) в результате получается положительное число. Ведь минус на минус дает плюс при умножении, сколько бы раз мы этот фокус не повторяли. Отрицательное число во второй, четвертой, шестой, восьмой и так далее степенях дает в результате положительное число.

Степень отрицательного числа

Таблицу квадратов или других степеней отрицательных чисел вы врятли встретите. Это уже тот уровень математики, когда вы должны пользоваться собственными знаниями.

Единица и двадцать один ноль

Единица и двадцать один ноль

Начнем считать по порядку.

1¹ = 1 - единица, единица в первой степени - она и в Африке - единица.
10¹ = 10 - а вот единица с одним нулем - это уже десять или десять в первой степени. В мире чисел это как аттестат о среднем образовании.
10² = 100 - десять во второй степени или единица с двумя нулями - это сто. Это уже кандидат числовых наук.
10³ = 1 000 - десять в третей степени или единица с тремя нулями - это тысяча. Всеми уважаемый доктор числовых наук.
10⁶ = 1 000 000 - десять в шестой степени, она же единица с шестью нулями, он же всеми желанный миллион. Что такое звание академика? Миллион баксов - вот это дело!
10⁹ = 1 000 000 000 - десять в девятой степени, единица и девять нулей. У нас и в дикой россии это число олигархов называют миллиард, в некоторых цивилизованных странах запада его иногда именуют биллион.
10¹² = 1 000 000 000 000 - десять в двенадцатой степени, единица с двенадцатью нулями. У нас и в дикой россии это конкретный триллион, в цивилизованных странах запада это число иногда обзывают всё тем же биллионом. Странные зигзаги цивилизации.
10¹⁵ = 1 000 000 000 000 000 - десять в пятнадцатой степени, единица и пятнадцать нулей, квадриллион или биллиард. Говорят, что математика - это точная наука. Судя по названиям чисел, в это верится с трудом.
10¹⁸ = 1 000 000 000 000 000 000 - десять в восемнадцатой степени, единица и восемнадцать нулей. Это произведение математического искусства называется квинтиллион.
10²¹ = 1 000 000 000 000 000 000 000 - десять в двадцать первой степени, единица и двадцать один ноль. Называется это число секстиллион.
10²⁴ = 1 000 000 000 000 000 000 000 000 - десять в двадцать пятой степени, единица и двадцать пять нулей называется септиллион. Тут явно произошел сбой ритма. Вместо трех нулей добавили четыре нуля.

Предлагаю на этом прекратить нашу экскурсию в мир буквенно-звуковых извращений математиков, так как дальше, на пути до дуомилиамилиамиллиона (10^6 000 003) можно наткнуться, упаси Боже, на дуцентдуомилианонгентновемдециллион. Впрочем, отметим еще парочку чисел.

10¹⁰⁰ = 1 000 ... 000 - десять в степени сто, единица и сто нулей. Называется это число гугол, я о нем уже упоминал в заметке о самом большом натуральном числе.
10¹⁰¹⁰⁰ = 1 000 ... 000 - десять в степени гугол, единица и гугол нулей. Сие произведение математического дизайна называется гуголплекс.

Как видите, нет предела математическим фантазиям. Учить все это наизусть не надо. Богаче мужа-миллиардера вам в жизни никто не угрожает. Я сам все эти названия самым бессовестным образом стырил из Интернета ("Десять миллионов знаков после запятой..." - была когда-то такая страница). Да и в Википедии есть таблица "Именные названия степеней тысячи", ну очень большая таблица. С огромным числом очень умных слов.

Так было на момент написания этой статьи. Сегодня (17.03.23г.) огромная таблица скромно спрятана в историю правок Википедии и осталась скромная табличка до числа 10 в степени 120. Но не это в таблице самое интересное.

Самое интересное в таблице то, что есть короткая и длинная шкала нулей. Число с одним и тем же названием по разным шкалам может иметь разное количество нулей. А вот в этом моменте уже очень четко прослеживается наша психология. Дело в том, что все числа до миллиарда включительно и по той, и по другой шкале имеют одинаковое количество нулей. Это такая страховка нищих землян от своих собратьев. В чем прикол? Представьте, инопланетяне одалживают у нас триллион долларов по длинной шкале ( с 18 нулями), а долг возвращают по короткой шкале (тот же триллион, но с 12 нулями). Нет, не потому, что они жадные или злые. Просто кто-то же должен дураков учить.

Если же кто-то когда-то начнет перед вами выпендриваться с непонятными названиями чисел, попросите его принести вам биллион капелек чая. Пусть чешет свою умную репу и думает, в какой посуде это подавать - в ведре или пожарной машине.

Самое большое натуральное число

Числа

Самого большого натурального числа нет и быть не может. Математики в таком случае говорят, что натуральный ряд чисел бесконечен. Так даже в Википедии написано.

Давайте разберемся, почему так происходит. Допустим, мы придумали самое большое натуральное число. Для простоты возьмем натуральное число "гугол" - это единичка с одной сотней ноликов, десять в сотой степени.

Да-да, не удивляйтесь, самая крутая поисковая машина Интернета Google названа в честь числа Googol! Оно и не удивительно, ведь создали поисковую машину в далеком-предалеком 1998 году два студента Лэрри Пейдж и Сергей Брин. Представляете, 12 (двенадцать!) лет назад не было Гугла! Как люди Интернетом пользовались?! Но мы немного отвлеклись...

И так, мы считаем, что самым большим натуральным числом является число Гугол. Что нам мешает дописать к этому самому большому числу ещё один, сто первый, нолик? Берем в руки ручку, оглядываемся по сторонам, чтоб никто не видел, и дописываем нолик. Наше самое большое натуральное число увеличилось в десять раз и стало еще больше! Круто! Дописываем еще нолик, а потом еще, и еще... Через время нолики писать уже некуда, а они (нолики) все никак не кончаются. Достаем следующий рулон обоев, приготовленных для ремонта прихожей, и продолжаем писать. На середине рулона заканчивается паста, а самого большого натурального числа мы так и не написали. Если скупить все шариковые ручки в киоске и все обои в строительном магазине, это сколько же ноликов можно дописать? Это будет самое большое натуральное число? Нет, строительных магазинов с обоями очень много, можно еще писать и писать... Забавно, конечно, потратить всю свою жизнь и все папикины деньги на писанину одного числа, но есть развлечения гораздо интереснее.

Давайте теперь посмотрим на проблему самого большого натурального числа с другой стороны. Если ребенок умеет считать только до пяти, то для такого ребенка число "пять" будет самым большим в мире числом. Но мы то хорошо знаем, что есть еще очень много чисел, которые больше числа "пять". Просто мы математику знаем гораздо лучше ребенка. Со временем ребенок сам будет смеяться над своим "самым большим в мире числом".

Нет никаких оснований не верить математикам, утверждающим, что ряд натуральных чисел бесконечен и самого большого натурального числа быть не может.

Пытался найти конструкцию самого большого числа, но даже всезнающая Википедия молчит на этот счет, а поиск по Интернету выдает разный мусор. Поэтому представляю свой собственный вариант САМОГО БОЛЬШОГО ЧИСЛА В МИРЕ. Это будет выглядеть как бесконечность в степени бесконечность, в степени бесконечность, в степени бесконечность... и так до бесконечности. Вместо значка бесконечности можете подставлять любое натуральное число, кроме единицы. Чем большее число вы подставите, тем круче будет взлет к недостижимому. Эта математическая конструкция называется бесконечная тетрация бесконечности:

∞^{∞∞∞···∞···}

Но и это не САМОЕ БОЛЬШОЕ ЧИСЛО В МАТЕМАТИКЕ, точнее, его математическая конструкция. Есть математические конструкции, в которых число взлетает в бесконечную высь ещё быстрые. Подобный принцип поиска самого большого числа гораздо эффективнее тупого дописывания ноликов, но в принципе ничем от него не отличается.

Кстати, маленькие числята, у которых выросло совсем мало ноликов, имеют довольно громкие имена собственные. Загляните на страничку "Единица и двадцать один ноль", если хотите познакомиться с ними поближе. Каждая блондинка обязана знать, чем миллионер отличается от миллиардера. Иначе как вы будете выбирать себе мужа?

С какого числа начинается натуральный ряд чисел?

Числа

Натуральный ряд чисел начинается с числа 1 (один). Число 1 (один, единица) является наименьшим натуральным числом.

В переводе на язык блондинок: самое маленькое натуральное число - это 1 (один, единица). У самого маленького натурального числа действительно два имени. Наверное, одно от папика, второе от мамика)))

Для лучшего запоминания натуральных чисел, вспомните, как мы считаем разные предметы: один, два, три... Мы тычем пальчиком в предмет и произносим его порядвовый номер. Начинаем мы считать всегда с единицы. Вот эти нехитрые наши действия математики положили в основу определения натуральных чисел. Ну, такое... Когда мы, вместо математики, начинаем плясать от себя, любимых, может возникнуть много разных вопросов и недопонимания. Вот смотрите.

Математики говорят, что натуральными являются те числа, которые возникли в результате естественного счета. Да, "один, два, три..." это один вариант чисел. Но самым естественным образом, в глубокой древности, появились и дробные числа, которые мы натуральными не считаем. Ведь делить добытого мамонта между членами племени - здесь одним натуральным рядом чисел не обойдешься. Для деления целого на части нужны дробные числа. Но на этом факте математики внимания не заостряют. От нас же требуется вызубрить определение и повторять его, как молитву.

Какие натуральные числа меньше пяти?

Числа

В ряду натуральных чисел есть четыре числа, которые меньше 5 (пяти). Это числа 1 (один), 2 (два), 3 (три) и 4 (четыре). Повторим для наглядности в крупном масштабе. Натуральные числа меньше пяти:

1; 2; 3; 4

Проверить правильность моих рассуждений можно, подсмотрев в таблицу натуральных чисел.

Для того, чтобы назвать следующее натуральное число, какое число надо прибавить к натуральному числу?

Для того, чтобы назвать следующее натуральное число, к имеющемуся натуральному числу надо прибавить 1 (один, единицу). Каждое последующее натуральное число на единицу больше рассматриваемого числа.

Следующее натуральное число

Ниже несколько математических примеров решения этой задачи.

Пример 1. Пусть у нас имеется натуральное число 3 (три). Какое следующее натуральное число? Для получения ответа прибавим к числу 3 (три) число 1 (один).

3 + 1 = 4

Ответ: натуральным числом, следующим за натуральным числом 3 (три) будет число 4 (четыре).

Пример 2. Дано натуральное число 16 (шестнадцать). Какое натуральное число следующее? Прибавляем к числу 16 (три) число 1 (один) и получим правильный ответ.

16 + 1 = 17

Ответ: натуральное число 17 (семнадцать) будет следующим за натуральным числом 16 (шестнадцать).

Пример 3. Какое натуральное число стоит за числом 18 592 (восемнадцать тысяч пятьсот девяносто два) в натуральном ряду чисел? К числу 18 592 (восемнадцать тысяч пятьсот девяносто два) прибавляем число 1 (один) и получаем следующее число из ряда натуральных чисел.

18 592 + 1 = 18 593

Ответ: число 18 593 (восемнадцать тысяч пятьсот девяносто три) стоит следующим за числом 18 592 (восемнадцать тысяч пятьсот девяносто два) в ряду натуральных чисел.

Общая формула для нахождения следующего натурального числа выглядит так (а плюс один равняется b):

a + 1 = b

где а - заданное натуральное число       b - следующее натуральное число.

Проверить полученный результат для первых 200 (двухсот) натуральных чисел можно по таблице натуральных чисел.