Вырожденный треугольник

В заключение мы проверим теорему косинусов для периметра на вырожденном треугольнике. Есть у математиков такая штучка. Чтобы получше в этой штучке разобраться, нам придется немного позаниматься фитнесом. Здесь может быть два случая. Становимся ровно, ноги на ширине плеч. Наши ноги образовали обычный треугольник, в котором сами ноги - это бедра равнобедренного треугольника, расстояние между пятками - основание треугольника. Теперь становимся в позу "пятки вместе, носки врозь" - у нас получился вырожденный треугольник. Вырожденным такой треугольник называется потому, что до полноценного треугольника ему чего-то не хватает. В данном случае - одной стороны. Нет, вырожденность - это не генетический сбой в наследственности треугольника. Это, скорее, увечье, полученное в результате милого общения с математиками. Хотя, гораздо уместнее здесь будет сравнение с религиозной практикой. У французских монахов кролик - это рыба (вера - верой, а жрать-то хочется, даже в Великий пост), у математиков отрезок - это вырожденный треугольник.

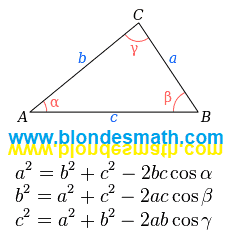
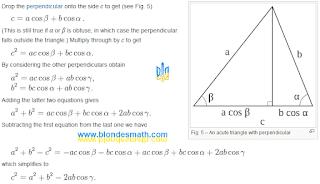
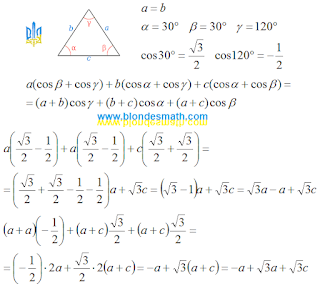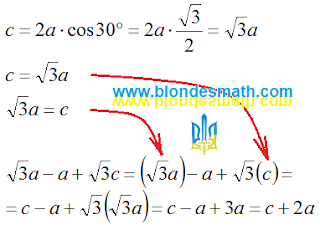Теперь упражнение по сдвиганию бедер проделаем с нормальным треугольником. Если мы уменьшим основание равнобедренного треугольника до нуля, мы получим два совпадающих отрезка. Сумма углов этого вырожденного треугольника равна 180 градусов. А как иначе? Он же треугольник! Угол при вершине становится равным нулю, значит углы при основании принимают значение 90 градусов. Два угла по 90 градусов дают в сумме 180 градусов - всё сходится.

Вырожденный треугольник

Как и следовало ожидать, периметр вырожденного треугольника (он же "два совпадающих отрезка", он же "один отрезок") оказался равен двум длинам его стороны. Напомню, мы считаем, что обе стороны такого вырожденного треугольника равны.

Рассматриваем второй случай. Вернемся к фитнесу. Ставим ноги в исходное положение - на ширину плеч. Раздвигаем ноги в стороны до тех пор, пока мы не сядем на поперечный шпагат. Свой подвиг я на ютуб не выкладываю - хвастаться нечем, признаюсь честно. Не многие читательницы могут это продемонстрировать. Про читателей я вообще молчу. Но в математике такой трюк выполняется элементарно просто - самим математикам на шпагат садиться не нужно.

Если мы совместим верхнюю вершину треугольника с основанием, мы получим второй вид вырожденного треугольника. Это отрезок, равный сумме двух других отрезков. Сумма углов здесь тоже равна 180 градусов, только теперь это величина всего одного угла.

Вырожденный треугольник

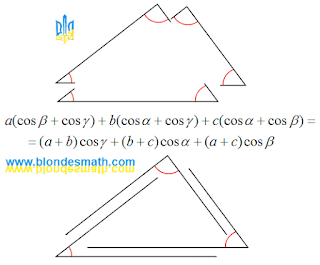
Как видите, в вырожденном треугольнике (он же "сумма отрезков") второго типа теорема косинусов для периметра работает безотказно. Почему после шпагата ноги разные? Так треугольники бывают не только равнобедренные, но и разносторонние.

Будем считать, что терему косинусов для периметра мы проверили на работоспособность и работает она безотказно. Одномерный отрезок (напомню, треугольник - это двухмерная геометрическая фигура) можно считать нижней границей применения теоремы косинусов. Где у теоремы косинусов верхняя граница? Для ответа на этот вопрос, мы перейдем к рассмотрению теоремы косинусов в общем виде.

Равнобедренный тупоугольный треугольник

Сейчас мы проверим, как выполняется теорема косинусов в тупоугольном треугольнике. Для примера (и для простоты) рассмотрим равнобедренный тупоугольный треугольник.

Равнобедренный тупоугольный треугольник

Упс! В периметре треугольника не может быть квадратных корней. Периметр этого треугольника равен сумме двух боковых сторон и основания. Что произошло? Закон косинусов не работает? Но такого быть не может - я верю в несокрушимую силу математики. Что-то здесь явно не так. Когда мы рассматривали треугольники с углами меньше или равными 90 градусов, никаких проблем не возникало. Когда мы взяли треугольник с углом больше 90 градусов - появились проблемы. Почему? Я всегда с большим подозрением отношусь к тригонометрическим функциям углов больших, чем 90 градусов. Здесь нужно подумать.

На решение этой задачи у меня ушло около получаса. Оказывается, секрет раскрывается очень просто. Давайте выразим основание треугольника через боковые стороны и посмотрим, что получится. Дважды вставим полученное равенство в наш результат. Первый раз вставляем сикось-накось, второй раз - накось-сикось. Вот что получилось.

Периметр треугольника

Как видите, всё чудесно сходится. Периметр получается таким, каким должен быть. У меня складывается такое впечатление, что тупой угол треугольника выворачивает на изнанку теорему косинусов. Заметьте, именно две одновременные подстановки приводят результат в божеский вид - минус на минус дает плюс :))) Оказывается, вот такое вот противоядие есть в математике против тупого угла.

Чтобы завершить проверку теоремы косинусов для периметра, рассмотрим вырожденный треугольник.

Равносторонний треугольник

Продолжаем проверку теоремы косинусов для периметра. Сейчас мы рассмотрим равносторонний треугольник. Все стороны равны, все углы равны. Прям, заповедник всеобщего равенства.

Равносторонний треугольник

Периметр равностороннего треугольника равен сумме трех сторон, всё чудненько сходится. Дальше мы проверим тупоугольный треугольник.

Уравнение с дробью

Что делать, если уравнение с дробью, а икс спрятан в знаменателе дроби? Кулинарный рецепт очень простой - нужно избавиться от знаменателя. А что будет с иксом? Не переживайте. Если делать всё правильно, он сам из знаменателя в числитель перелезет. Здесь можно порекомендовать два способа приготовления блюда, то есть решения уравнения.

Первый способ заключается в приведении выражения к обычной пропорции. Дальше по свойству пропорции - произведение крайних членов пропорции равно произведению средних членов пропорции. Знаменатели дроби волшебным образом исчезают и у нас появляется банальное уравнение, которое мы должны легко решить. Во всяком случае, так думают учителя и тупые бюрократические функции из министерства образования. Рассмотрим пример. Решения я записываю подробно: с чувством, с толком, с расстановкой :))) Математики рекомендуют сокращать записи. Для экономии бумаги в тетрадках это очень полезно, но... Записать условие задачи и тупо переписать ответ из решебника - это тоже сокращенный вариант записи решения. С другой стороны, при сокращенной записи решения у меня всегда возникают подозрения, что меня хотят обмануть. Ведь математика - наука точная: два раза соври, получится правда.

Уравнение с дробью

Что-то число у меня не сильно красивое получилось. Обычно математики любят, чтобы в результате всё сокращалось, упрощалось, а здесь - нет. Ладно, сделаем проверку и посмотрим на результат. Подставляем в первоначальное выражение вместо икса его значение.

Проверка уравнения

Проверка показала, что блюдо получилось превосходного качества и полностью готово для подачи на стол учителя.

Второй способ заключается в приведении выражения к общему знаменателю. Знаменатель должен быть общим для левой и правой частей равенства. В этом случае мы с чистой совестью можем выбросить знаменатель в мусор. Ведь как гласит математика, которую мы никогда не должны забывать (как наивно полагают учителя), если две дроби равны и имеют равные знаменатели, то числители этих дробей так же равны. Может, в учебниках по математике так не написано, но смысл равенства дробей в этом и заключается. Я-то уже давно забыл, чему меня там учителя учили. Смотрим пример приведения к общему знаменателю.

Уравнение с дробью

Результат получился таким же, как и в первом случае. В этом и заключается прелесть математики - мы можем делать так, как нам нравится, но результат всегда будет один и тот же. Кстати, это правило касается только свободных разумных существ. Ученики должны делать так, как требуют учителя. Иначе у учеников возникнут большие проблемы - тупые бюрократические функции очень не любят, когда им не подчиняются.

Прямоугольный треугольник

Сейчас мы проверим теорему косинусов для периметра на примере прямоугольного треугольника. У прямоугольного треугольника один угол равен 90 градусов, косинус этого угла равен нулю. Косинусы остальных углов получаются делением длины гипотенузы на длину прилежащего катета. В общем виде проверка теоремы косинусов выглядит так.

Прямоугольный треугольник формула

Смотрите, как всё чудненько получается - периметр треугольника действительно равен сумме трех его сторон. Но это буковки, а как с числами? Давайте подставим в формулу длины сторон прямоугольного треугольника и значения косинусов углов. Для примера возьмем пифагорову тройку чисел для значения длин сторон. Косинус угла определяем как отношение прилежащего катета к гипотенузе.

Прямоугольный треугольник пример

Полученные значения равны периметру треугольника. Теорема косинусов позволяет проверить треугольник на разрыв. Вот что получится, если одна из сторон не доходит до вершины треугольника.

Разорванный треугольник

Равенство выполняется, но результат не равен сумме длин отрезков ломаной линии или периметру воображаемого треугольника. А что будет, если мы неправильно запишем данные? Ну перепутали чуть-чуть, с кем не бывает. Поменяем местами значения косинусов углов, а длины катетов прямоугольного треугольника запишем правильно. Любуемся результатом.

Неверные измерения

А полученный результат не совпадает со значением периметра. Где это можно использовать? В геодезии, например. Если измерить три расстояния между точками на местности и три угла, то по теореме косинусов для периметра можно проверить правильность этих измерений. Но мы со своей математикой немного опоздали. Сделаем маленькое лирическое отступление и вспомним историю.

Лет сто назад война обычно начиналась из геодезических измерений будущего театра военных действий. Математика позволяла определить траекторию полета снаряда, но, без знания точного рельефа местности, трудно определить, куда именно снаряд попадет. Вот рельефом местности геодезисты и занимались. С математикой они особо не заморачивались. Если в измерениях появлялась незначительная ошибка, то ошибку делили на три части и равномерно распределяли по трем измеренным углам или по трем сторонам. Таким образом фактические измерения подгонялись под математику. Для эффективного убийства себе подобных этого вполне хватало. Сегодня геодезисты уже не бегают с инструментами перед началом войны. Достаточно достать из архива старые карты прошлых войн и раздать их своим солдатам-отпускникам, чтоб они хорошо знали, где именно им нужно заблудиться.

На этом покончим с прямоугольным треугольником и перейдем к его равностороннему собрату.

Теорема косинусов для периметра

Внимательно посмотрим на доказательство теоремы косинусов и сделаем некоторые поправки.

Анализ доказательства

Добавим в треугольник ещё две высоты, что бы можно было каждую из сторон выразить через две другие. Избавимся от ненужного возведения во вторую степень и, самое главное, в предпоследней строке поменяем знак "минус" на знак "плюс". Теперь мы можем записать теорему косинусов для периметра треугольника.

Теорема косинусов для периметра

Получилась очень простая и красивая формула, которая описывает сразу весь треугольник. Теперь не нужно делать циклические перестановки или менять обозначения на картинке треугольника. Сама формула содержит цикличность. Лично я считаю эту формулу одним из математических шедевров - простая, легкая для запоминания. Очень жаль, что до сего времени эта жемчужина математики оказалась не востребованной, иначе она уже давно была бы в учебниках. И садисты-учителя применяли бы эту врожденную красоту для пыток и издевательства над учениками.

Теорема косинусов для периметра выражает зависимость между углами и длинами сторон в треугольнике.

Геометрия теоремы косинусов

Если в доказательстве теоремы косинусов язык, на котором доказательство написано, был для нас не особо важен, то приведенная выше картинка лишена даже языковых признаков (если не обращать внимания на буквы формул). Такую картинку можно смело инопланетянам показывать и они её, скорее всего, поймут. Сомневаюсь я, что инопланетяне, которые смогут прилететь к нам, будут плохо знают математику. О наших собственных полетах к инопланетянам я даже заикаться не буду - нам до этого ещё расти и расти. На теории множеств и математических определениях далеко не улетишь.

Закон косинусов для периметра описывает периметр треугольника, составленного из одномерных евклидовых пространств (отрезков). Для многомерных пространств закон косинусов имеет другой вид. Но прежде, чем переходить к многомерности, проверим теорему косинусов для периметра на прочность. А начнем мы проверку с прямоугольного треугольника.

Больше о новых взглядах на математику и её проблемах смотрите на странице "Новая математика"

Теорема косинусов

То, что я собираюсь вам рассказать, вы не найдете в учебниках. Вас никто не будет спрашивать об этом на уроках и на экзаменах. Возникает естественный вопрос - зачем вам это нужно? Разумные существа должны знать больше того, чему их учат. На примере теоремы косинусов, о которой я уже писал здесь, вы увидите, как можно пользоваться математикой.

Треугольник имеет три стороны и три угла. Внешний вид теоремы косинусов зависит от принятых обозначений углов и сторон треугольника. Для описания одного треугольника нам нужно три раза записать теорему косинусов, для каждой стороны отдельно.

Теорема косинусов

Три стороны (и три угла) треугольника дают три варианта формулы для одного треугольника. В теореме косинусов можно использовать одну формулу и три варианта обозначений.

Варианты обозначения треугольника

Оба подхода позволяют описать все стороны и углы треугольника. Но для этого требуется либо три формулы, либо три картинки. В традиционных задачах по математике нас учат находить один из элементов треугольника.

Вопрос: Можно ли одной формулой с одним вариантом обозначений описать все элементы треугольника?

Ответ: Да, можно.

Рассмотрим, как это сделать при помощи теоремы косинусов. Доказательство теоремы косинусов в тригонометрической форме выглядит так.

Доказательство теоремы косинусов

Не смотря на то, что доказательство на английском языке, вы без труда в нем разберетесь, поскольку язык математики универсальный для всей нашей планеты. Так вот, если в этом доказательстве изменить знак «минус» на знак «плюс», мы получим теорему косинусов для периметра треугольника.