Теорема косинусов в общем виде

ффф

Теорема косинусов в общем виде для любого треугольника в евклидовом пространстве выглядит так.

Теорема косинусов в общем виде

Первая формула теоремы косинусов описывает периметр и устанавливает его зависимость от сторон и углов треугольника. Вторая формула - это двухмерный вариант теоремы косинусов. Последняя формула представляет многомерный вариант теоремы косинусов для треугольника в евклидовом пространстве с любым количеством измерений. Данная формула позволяет учитывать влияние кривизны пространства в любых пространственных направлениях при переходе от евклидового пространства к не евклидовым и обратно.

Теорема косинусов для треугольника в не евклидовом пространстве будет иметь более громоздкий вид. Каждый геометрический элемент формулы, представленный в виде степени, может быть представлен в виде сомножителей, имеющих свои собственные коэффициенты кривизны пространства.

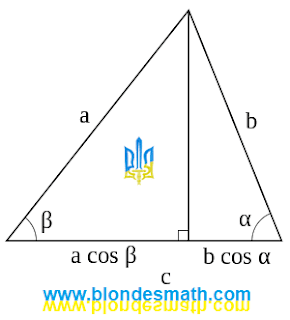
Формула периметра треугольника может быть представлена в двух различных видах. В одном случае периметр можно выразить через сторону и сумму косинусов прилежащих углов. В другом случае это можно сделать через сумму двух сторон треугольника, умноженную на косинус угла между ними.

Теорема косинусов для периметра треугольника

Геометрическое изображение теоремы косинусов для периметра треугольника можно представить следующим образом. Это ещё одна картинка, которая поможет установить взаимопонимание между нами и инопланетянами.

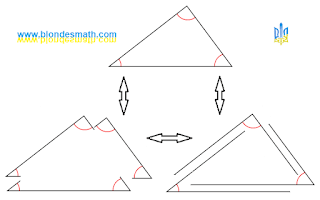Теорема косинусов

Математики говорят, что теорема косинусов является обобщением теоремы Пифагора. Они ошибаются. Теорема косинусов описывает зависимости между сторонами и углами треугольника в пространстве. Теорема Пифагора описывает несколько другие вещи. Многомерность в этих двух теоремах так же реализуется по-разному. В теореме косинусов задействованы показатели степеней, в теореме Пифагора количество пространственных измерений связано с числом слагаемых в формуле.

Теорема косинусов в общем виде является не просто набором математических символов, это безупречно работающая динамическая система. Некоторые моменты в работе теоремы косинусов мы рассмотрим более подробно.

Больше о новых взглядах на математику и её проблемах смотрите на странице "Новая математика"

Теорема косинусов

Рассмотрим теорему косинусов в её классическом виде. Берем произвольный треугольник и записываем саму теорему.

Теорема косинусов

При решении задач нужно помнить, что для одного конкретно взятого треугольника теорема косинусов может быть записана в трех вариантах.

Три варианта теоремы косинусов

Как видите, теорема косинусов позволяет определить все три угла треугольника, если нам известны длины его сторон. Даже при современном уровне развития техники, измерить длину гораздо проще, чем измерить угол. Вот здесь теорема косинусов может оказаться очень даже полезной.

Это было маленькое лирическое вступление. А теперь сама история. Не помню, что мне было нужно, но попал я на страницу Википедии, где рассказывается о теореме косинусов. Как-то я уже говорил, что на англоязычных страницах Википедии математика представлена более полно и интересно, чем на русскоязычных. Заглянул я к иностранцам и в этот раз. Там меня заинтересовала одна картинка. Вот она.

Иллюстрация к теореме косинусов

Рядом приводится доказательство теоремы косинусов, которое меня очень заинтересовало. Вот как оно выглядит. Ничего, что текст на английском языке. Настоящая математика в переводчиках не нуждается.

Доказательство теоремы косинусов

Вникнув в смысл доказательства, я начал просматривать всю страницу. Признаюсь честно, я был в шоке. Как?! И это всё???!!! А что, пошевелить собственными мозгами так никто и не додумался? Дело в том, что предлагаемый ход рассуждений позволяет вывести теорему косинусов в общем виде. Неужели за две тысячи лет никому из математиков это не пришло в голову?

Взяв в руки листок бумаги и карандаш, я тут же набросал очень симпатичную формулу. Пару дней я её крутил и так, и этак, пока не поймал себя на мысли, что я повторяю ту же ошибку, которую математики совершали тысячелетиями - я тупо повторяю чужие действия и рассматриваю формулу исключительно в общепринятом виде, собственные мозги я вообще не включаю. Еще раз посмотрев на доказательство теоремы, до меня наконец-то дошел её настоящий смысл. Пара часов работы и теорема косинусов в общем виде была готова. Теперь мы можем познакомиться с нею поближе.

Как не менять знаки внутри скобок?

Автор Николай Хижняк

Всех нас учат менять знаки при раскрытии скобок или закрывании части выражения в скобки, если перед скобками стоит знак минус. Давайте рассмотрим этот нудный процесс на полуживых примерах.

11-(2+5-4) = 11-3 = 8

Перед выражением в скобках стоит знак минус, это значит, что при раскрытии скобок нужно поменять все знаки на противоположные у всех чисел, которые находятся внутри скобок. Этот же пример, но уже без скобок.

11-(2+5-4) = 11-2-5+4 = 9-5+4 = 4+4 = 8

Теперь попробуем взять часть выражения в скобки. Рассмотрим другой пример.

1+2+3+4 = 10

Естественно, вы спросите: "Где же здесь знак минус?!" Не переживайте, сейчас появится.

1+2-(-3-4) = 3-(-7) = 3+7 = 10

Я поставил перед скобками знак минус и поменял знаки перед числами внутри скобок. При раскрытии скобок я снова поменял знак на противоположный, поскольку у меня перед скобками стоит знак минус. В итоге результат остался неизменным.

Теперь более заковыристый пример.

17-6+9 = 20
17-(6-9) = 17-(-3) = 17+3 = 20

Как видите, сплошная головная боль получается, если вдруг перед скобками появляется знак минус. Как не менять знаки внутри скобок? Очень просто - не нужно ставить минус перед скобками. Вот смотрите, как это делается.

17-6+9 = 17+(-6+9) = 17+(3) = 17+3 = 20

Теперь рассмотрим два последних примера под микроскопом. В первом случае я поставил первую скобку после знака минус. Я словно ножом разрезал отрицательное число на две части - знак минус и положительное число. Знак минус оказался перед скобкой, а положительно число - внутри скобок. Посмотрите.

17-(6........

Фактически мы в скобки заключаем положительное число, которое до этого было отрицательным. Изменение знака перед первым числом внутри скобок прошло на полном автопилоте без всякого нашего вмешательства. Такой себе автомат по обрезанию знака минус у чисел. А вот с остальными числами, попадающими в такие скобки, уже возникают проблемы. Знаки у них нужно менять вручную.

Во втором случае я поставил открывающую скобку перед знаком минус. Фактически я заключаю в скобки отрицательное число вместе со знаком минус. Вот как это выглядит первоначально.

17(-6.........

Теперь между числом 17 и скобкой нет никакого знака, что в математике подразумевает умножение. Но мне не нужно ничего умножать. Чтобы ответ при решении примера оставался прежним, я ставлю перед скобкой дополнительный знак "плюс".

17+(-6.........

Вот теперь всё правильно записано. Перед скобками появляется знак полюс и знаки перед числами внутри скобок менять не нужно. Никакого математического преступления я не совершаю, просто грамотно избавляюсь от лишних действий по замене знаков внутри скобок. Почему математики всегда так не делают? Их никто этому не учил. Если этого нет в учебной программе, то и учить вас этому никто не будет. Математику мало знать, нужно ещё уметь нею пользоваться.