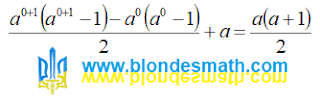Я давно изучаю тригонометрию. Те тригонометрические преобразования, которые я вам сейчас покажу, лично для меня находятся где-то в основании математики. В тех утерянных страницах учебников по математике, которые предшествовали натуральным числам. Или которые нам ещё только предстоит написать. Вопрос ко всем вам: без понимания чего не могло возникнуть само понятие счета?
Тригонометрия
Это маленькое лирическое отступление для тех математиков, которые давно уже забыли тригонометрию. Какой уважающий себя математик будет заниматься такой давно известной ерундой, как тригонометрия? Специально для них я напоминаю:
 |
| Тригонометрия формулы |
Школьники хорошо знают эти тригонометрические формулы. Они проверены практическим применением на протяжении сотен лет. Многие поколения математиков без особых проблем применяли эти тригонометрические преобразования. У меня нет никаких основания сомневаться в правильности этих тригонометрических формул.
Но в этих формулах заложена одна маленькая задача, решение которой оказалась не по зубам всем поколениям математиков. Называется эта задача «деление на ноль». Сейчас мы посмотрим, как она выглядит в тригонометрических формулах.
Деление на ноль
Теперь мы будем подставлять значения тригонометрических функций при разных значениях углов в приведенные тригонометрические формулы. Никаких особых проблем при этом не возникает, за исключением углов, равных 0 и 90 градусов. Посмотрим, что при этом получается:
 |
| Тригонометрия и деление на ноль |
Тригонометрические формулы однозначно показывают, что:
1. В результате деления нуля на ноль получается единица.
2. Деление числа (единица) на ноль возможно.
В возможность деления числа на ноль я долго не верил. Совсем недавно я решил и эту задачу. Сейчас нужно всё красиво оформить и опубликовать. К сожалению, всё мое время занято зарабатыванием денег для существования, а не решением математических задач.
Кстати, в возможность деления на ноль я верю очень давно. Именно эта вера заставила меня заняться тригонометрией. Я не знал тригонометрию ни в школе, ни в институте. Именно понимание тригонометрии позволяет найти решение задачи по делению на ноль. Достаточно знать, что и где искать. Что нужно искать, вы уже знаете. Где нужно искать, я вам скоро покажу вместе с основными принципами деления на ноль.
Порядок выполнения математических действий
и результат деления на ноль
Теперь вернемся к маленькой проблеме, состоящей в том, что деление нуля на ноль имеет разные результаты в разных формулах: в тригонометрических формулах и в формуле преобразования площади трапеции. Вполне возможно, что результат зависит не от математических действий, а от порядка выполнения умножения и деления.
Напомню, что по правилам математики умножение и деление выполняются в том порядке, в котором они записаны в математическом выражении. Кто записывает математическое выражение? Математик. На каком основании? А вот это уже вопрос интересный. В идеальном случае порядок математических действий должен определяться физическим процессом, который описывает математическое выражение. По факту же, в каком порядке математик захочет, в таком и запишет. Но давайте посмотрим, что я имею ввиду:
 |
| Математические действия и деление на ноль |
На мой взгляд, такой вариант лучше вписывается в математические правила. Но определяющим фактором будет результат практического применения этих теорий в будущем. Почему результат деления единицы на ноль я обозначил «х»? Каким бы он ни был, в результате умножения на ноль мы получим ноль.
Вывод
Авторитетно заявлять я не имею ни морального, ни юридического права. У меня нет ни авторитета, ни математического образования и к математике я не имею никакого отношения. Математика – это моё хобби. Но это является моим главным преимуществом. Я могу говорить всё, что считаю нужным. Ни с учебного заведения, ни с работы меня за это никто не выгонит. Поэтому, как существо разумное, я вам скажу следующее.
Математики совершенно правы, когда говорят, что деление на ноль невозможно. В рамках теории чисел эту задачу никто не смог решить и вряд ли сможет. Теория множеств вообще к математике никакого отношения не имеет. Какие ещё инструменты есть у математиков для решения задачи по делению на ноль? Геометрия? Или что-то ещё?
Я считаю, что главная ошибка математиков заключается в глобальном подходе к решению задач. Математики всегда всё обобщают и расширяют. Правильный научный подход предполагает так же умение разобщать и сужать. Без этого наука превращается в заурядную религию. Современные математики не способны даже слагаемые пальцем посчитать при перестановке слагаемых в сумме. Ну и что, что эта сумма бесконечная? Законы математики всегда, везде и для всех одинаковы. У меня ещё очень много вопросов к математикам по типу «Почему именно так, а не иначе?». Надеюсь, я успею их сформулировать.
Больше интересных математических идей на странице "Моя математика"