Зверёк

Автор Николай Хижняк

Фантастический рассказ

Аэра внезапно проснулась среди ночи. Ей приснились глаза. Глаза безымянного зверька с этой обреченной планеты. В последнее время эти глаза внимательно следят за нею из кустов возле её дома. Теперь эти глаза начали следить за нею и во сне. Что всё это значит? Ведь не просто так этот сон повторяется уже третий раз за последнюю неделю. До рассвета остается ещё час, и она больше не уснет. Это Аэра уже знала по опыту.

Аэра заблокировала свои мысли и приступила к анализу ситуации. Этот её поступок бесстрастно зафиксировал коммуникатор - телепатический прибор, который фиксирует всё, что бы она ни делала. Ну и пусть. Утром психологи снова будут с подозрением изучать собранные о ней данные. Её могут отстранить от работы. Этого она боялась больше всего. Что она тогда будет делать? Об этом не хотелось думать. Что делать сейчас? Три неполноценных сна за одну неделю – это уже слишком. Особенно для пилота летающей тарелки. Будь Аэра на месте психологов, она бы, не задумываясь, отстранила себя от полетов.

Но сейчас несколько другая ситуация. За нею следят всегда и везде. Как и за всеми остальными. Коммуникатор в летающей тарелке фиксирует мельчайшие подробности её поведения. Если бы недосыпание предыдущих ночей сказалось на её реакциях, её бы уже отстранили от управления аппаратом. Значит, до сих пор всё было нормально. Ей остается только надеяться, что нормально будет и сегодня.

Почему она думает о психологах? Раньше она почти никогда не встречалась с ними и вообще никогда не думала. Да, пару раз её отстраняли от полетов. После этого был отдых в течение нескольких недель и снова работа. Тогда это была просто усталость. Грандиозные катастрофы на обитаемых планетах… Срочная эвакуация жителей… Большое количество ученых, изучающих природный процесс… Тогда пилотам разрешали спать на два часа меньше, чем сейчас, и просто заменяли свежими пилотами по указанию психологов. В целях безопасности. Сейчас такой возможности нет. Те операции длились не больше недели. На этой планете собрали всех самых лучших пилотов. Вот уже месяц они работают и днем, и ночью. За всеми ими непрерывно следят психологи. Обеспечивают безопасность и попутно изучают поведение в экстремальных ситуациях. Бесценный опыт на будущее…

…И тут она со своими проблемами. Да, проблема именно в ней. Это Аэра поняла сейчас очень четко. Что-то в глубинах подсознания ищет выход и не может найти зацепку в сознании. Только глаза зверька… Она должна понять что-то очень важное, чего она сейчас не понимает. Это не связано ни со зверьком, ни с ситуацией на планете. Это непонимание началось гораздо раньше и накапливается в ней годами. Последние события только усугубили проблему. Какая-то случайная ассоциация всколыхнула её подсознание, и появились эти тревожные сны… Глаза зверька, наблюдающего за нею… Нет, это не коммуникатор, это не психологи, это не её повседневная работа… Это что-то совершенно постороннее… Но почему здесь и сейчас? Что означают эти глаза? Ведь её со зверьком ничего не связывает, кроме…

Аэра словно очнулась от гипнотического транса. …Ничего не связывает, кроме совместного места проживания. Да, они живут на этой плате рядом и эта планета скоро погибнет. Аэра благополучно переселится на другую планету, а что будет со зверьком? С её Зверьком?!

Аэра вскочила с кровати и начала ходить по комнате. Нужно что-то делать. Но что именно? Она прекрасно понимала, что от дальнейших её действий зависит то, найдет она ответ на свой вопрос или нет. Если она всё сделает правильно, она скоро будет знать не только ответ, но и сам вопрос… Аэра внезапно остановилась... Ну да, она даже сам вопрос сейчас не может сформулировать. Что она не знает такого, что знать хочет? Глубоко в ней что-то очень хорошо спрятано. Настолько глубоко, что вообще не за что ухватиться… Только эти глаза Зверька… Она должна забрать Зверька с собой! Вот то решение, которое, несомненно, отразится на всей её дальнейшей жизни. Правильное это решение или нет, она не знала. Но ей уже было всё равно. Рано или поздно она докопается до сути и вопроса, и ответа.

Продолжение следует

Деление на ноль окончание

Начало теории деления на ноль, которую написал Сергей Манулов, смотрите здесь.

Теперь наш человек-экспериментатор решил посмотреть, что будет, если принести цветной шарик из правой комнаты в левую. Он взял синий шарик 5, и принёс его в левую комнату. Для условности договоримся, что пока шарик какого-либо цвета находится в руках человека, он никак не влияет на количество шаров внутри комнат. И вот человек кладёт синий шарик в комнату, где лежат чёрные шарики. Что происходит? Чёрные шарики все исчезли из комнаты. Это произошло из-за того, что существование материи доказывает не существование пустоты по определению. Чёрные шарики могут существовать, только если нет цветных шариков. Но вот цветные шарики самим фактом своего существования, полностью перечёркивают возможность существования чёрных шариков. Поэтому, когда человек взял в руки синий шарик, в тот же час вновь появились чёрные шарики. Да и унёс он синий шарик в третью комнату, от греха подальше. Затем комнату, как и в предыдущие разы, он очистил.

Теперь человек пошёл в правую комнату, посмотрел на синий шарик, подумал-подумал и решил не брать его и шарики другого цвета тоже. Но, ему ведь нужно что-то принести в третью комнату, таково его задание! Тогда он пошёл в левую комнату и взял чёрный шарик, один, два, три, неважно сколько, главное для него выполнить условие.

В третьей комнате в итоге теперь лежит чёрный шарик. Его, кстати, можно не только объединять в один шарик, но и вытаскивать из него любое произвольное число (кроме нуля) чёрных шаров. Воистину удивительны его свойства!

Математическая запись: 5*0=0. В общем случае n*0=0, где n – любое отличное от нуля число.

Очистив комнату, человек пошёл проделать такой же опыт с левой комнатой. Он посмотрел на чёрный шарик и решил его не брать. Затем он пошёл в третью комнату и обнаружил, что в его руках находится чёрный шарик! Но откуда? Неважно, он положил его в третью комнату. Математическая запись: 0*0=0.

Но, человек призадумался, откуда взялся шарик? Он не брал его и затем вернулся в третью комнату, так как по условию, в третьей комнате всегда должен находится какой-либо шарик, изначально же в ней нет шариков, их туда приносит только человек. Тогда откуда взялся чёрный шарик?

Человек очистил комнату, пошёл в правую комнату. Посмотрел на синий шарик, и сразу вернулся в третью комнату. В руках у него ничего не было, он ведь ничего не взял из левой комнаты. Он не выполнил задачу. Тогда он стал думать, 0*0=0. Откуда берётся шарик, если он его не брал? Действительно откуда? Тут закралась какая-то ошибка. И тут он вспомнил, что когда он выходил из левой комнаты, он ударился головой, в состоянии аффекта, он взял один шарик и вошёл в третью комнату. Аффект прошёл, но он забыл о содеянном. Получается тогда, что он всё-таки взял шарик? Именно так.

Человек вошёл в левую комнату. Он решил не брать чёрный шарик. Но как это сделать? Стоп! А что он делал, когда не брал цветные шарики? Шёл в соседнюю комнату! Так, почему бы не поступить и сейчас так же? Он вошёл в правую комнату, и взял синий шарик и отнёс в третью комнату. Там теперь находится один синий шарик – 5. Математическая запись: 0*0=5.

Человек множество раз повторил этот эксперимент, но с разными шарами. Каждый раз, когда он не брал чёрный шарик, он брал цветной шарик. Он сумел выполнить условия задания, беря произвольное число шаров. Математическая запись: 0*0=n, где n – любое отличное от нуля число.

Это уравнение вытекает из-за самого определения: если пустота (0) не существует (не берётся в третью комнату), то тогда существует материя (цветной шарик, то есть любое число не равно нулю). Всё просто.

0*0=0

Ноль, умноженный на ноль, равняться нулю не может. Сами посудите, эта запись эквивалентна выражению: пустота, взятая ни разу, есть пустота. Это противоречит предыдущим формулам, где 0*n=0, то есть пустота, взятая любое число раз, за исключением нуля, получится пустота. Это её фундаментальное свойства. Мы же с вами заметили, что чёрный шарик может дробиться на бесконечное число точно таких же чёрных шариков, или слипаться в один чёрный шарик такого же размера. Цветные шарики слипаться и дробиться тоже могут, но меняется и их цвет и размер. Можно раздробить один цветной шарик, на равные шарики по размеру и цвету, но их размер и цвет будет отличен от цвета исходного шарика. Таковы свойства материи.

Теперь мы получили уравнения:

0*0=n , ноль как качество (пустота) взятая ни разу (0 раз) – есть любое качественное число, отличное от нуля. Тоже самое равносильно и для раз: ни разу ни разу равняется раз. Двойное отрицание.

n*0=0, любое отличное число от нуля (n) взятое ни разу (0 раз), есть ноль как качество, то есть ничто – пустота. С разами тоже самое: раз ни разу = ни разу. 0*n=0, ноль как качество (пустота) взятое произвольное количество раз, за исключением ни разу, есть ноль – пустота, то есть качество. С разами то же самое: ни разу раз = ни разу. Ну а теперь самое приятное – деление на ноль!

Запишу ещё раз эти формулы:

0*0=ё, 0*ё=0, ё*0=0, где ё=n (ранее) - любое число, отличное от нуля. Почему ё? Мне нравится эта буква, не хочу, чтобы она исчезла вот и увековечиваю её таким образом. Получаем: 0/0=ё, ё/0=0, 0/ё=0. Получилась замкнутая и красивая система.

Теперь проанализируем физический смысл на примере: 6/3=2, означает, что 6 (качество) содержит в себе качества 2 три раза. Или: 6 (качество) содержит в себе качества 3 два раза.

6/0=0, означает, что 6 (качество) содержит в себе качества 0 ноль раз. Или: 6 (качество) содержит в себе качества 0 ноль раз.

Логично, что 6 не состоит из нулей. Поскольку материя – состоит из материи, не пустоты. Пустоты в природе не существуют, как абсолютная. Локальная – возможно, но её, пока что, никто не открыл. Даже физический вакуум – есть так называемое море Дирака, оно состоит из виртуальных частиц, которые друг друга уравновешивают.

0\0=ё так же имеет смысл. Это означает, что ноль состоит из нулей произвольное число раз, за исключением ни разу. Ноль не может состоять из какого-либо числа, кроме нуля. Ё – это не конкретное число, это любое число отличное от нуля. Для каждого уравнения оно своё.

Вот пример:

0=0
25 - 25 = 20 - 20
5(5 - 5) = 4(5 - 5)
5(0) = 4(0)
5(0/0)=4(0/0)

В данном случае, 0/0 в левой части не равен 0/0 в правой. Запись одна, а результаты разные. Это прямо тогда с чёрными шариками, мы можем извлечь из одного чёрного шарика – любое число чёрных шариков. В этом уравнении 0/0 – это не качество, а обозначение количества (разы), просто такая вот запись. В нашем мире не существует 0 как качества, то есть пустоты. Из определения того, что есть материя. Мы существуем в материальном мире. Иными словами, когда мы умножаем на ноль или делим на ноль – взаимодействуем с разами и только разами, но никак не с качеством.

0*0=0/0=ё.

Остальные операции можете вывести сами.

Математика безграничная наука, и только мышление без границ может помочь её освоить. Любую критику и замечания шлите по этому емайлу prebereda@sibmail.com.

(Николай Хижняк: Полная ёрунда. Душещипательная эпопея по перетаскиванию шариков из комнаты в комнату под общим названием «Мартышкин труд». Лично я ничего не понял, а только заблудился в лабиринте из трех комнат и двух понятий – количество и качество. Ноль левый, ноль правый – это я у математиков уже встречал.

Что касается деления нуля на ноль. Математикой никто пользоваться не пробовал? Там есть очень логичный вывод 0/0=1. Не из пальца высосанный, а из формулы, которой все пользуются не один десяток, а то и сотни лет. Именно такой результат деления нуля на ноль приводит к правильному решению. Это как называется? Неправильная формула? Шаманы от математики скрывают свои тайные знания? Или математики математикой пользоваться не умеют?)

Деление на ноль эксперимент

Начало этой теории деления на ноль, которую написал Сергей Манулов, смотрите здесь.


Поскольку деление на ноль - действие достаточно неочевидное и труднопонимаемо из-за своей специфики, чтобы объяснить его сущность, прибегу к образной аналогии.

Представим 3 комнаты, сделанные из не материи и не пустоты. Конечно, такое вещество не существует, но это лишь образ, допущение, которое позволит нам строить аналогию. В левой комнате имеется бесконечное число чёрных бильярдных шариков, которые символизируют пустоту, которую обозначим числом 0. То есть, каждый шарик чёрного цвета есть число 0, причём нужно помнить, что эта пустота (0) есть качество, а не количество.

В правой комнате находятся цветные шарики, их бесконечно много, каждый цвет – это определенное число, рациональное, иррациональное, положительное и отрицательное. Единственного шарика там нет – чёрного, то есть, нет числа 0 (Николай Хижняк: Вот и я ещё раз повторяю - ноль не является числом). Допустим 1 – это сиреневый шарик, 2 – красный, 5 – синий и так далее…. Чтобы не захламлять комнаты, будем считать, что в них есть аппарат, который выдаёт шарик нужного цвета, при вводе числа. Эти числа так же обозначают качества. В левой комнате аппарат выдает только чёрные шарики, а в правой любые другие, кроме черного.

Третья комната абсолютно пустая, в ней нет шариков. Она будет нашим складом, то есть мы будем брать шарики из первых двух комнат и приносить в третью. Предположим, в комнате есть механизм, очищающий её от шариков.

Между комнатами есть двери, через которые может проходить человек, который так же состоит из не материи и не пустоты. Он будет брать шарики или из левой комнаты, или из правой, или сразу из двух. Но перед тем как мы начнём эксперимент, мы должны изучить и понять свойства шариков, как чёрных, так и цветных.

Пустота по определению – это то, что существует тогда, когда не существует материя. Материя – это то, что существует тогда, когда не существует пустота. Из этих определений вытекает, что когда существует чёрный шарик, не существуют цветные шарики и наоборот. Благодаря этому мы имеем ряд интересных и необычных свойств черного шарика, суть которых раскроется позже.

Человек, выходя из третьей (пустой) комнаты, входит либо в левую, либо в правую комнаты. В пустую комнату он всегда будет что-то приносить в руках, либо чёрный шарик, либо цветной. Третья комната символизирует то, что получается после знака равно в математических уравнениях.

И так начнём эксперимент.

Человек входит в правую комнату и берёт один шарик синего цвета (5) один раз, затем он вносит это в пустую комнату. В третьей комнате находится синий шарик. Математическая запись этого действия: 5*1=5. Договоримся, что первая цифра будет означать качество, а вторая количество (разы). Знак после равно означает то, что имеется в третей комнате в итоге. Человек очистил комнату и вновь пошёл за шарами, но теперь в левую комнату.

Человек взял 2 чёрных шарика, случилось необычное явление, эти шарики как бы слились в один. Он отнёс новый шарик в третью комнату. В итоге теперь там находится чёрный шарик. Математическая запись: 0*2=0. Человек ещё пару раз сходил в левую комнату, и сколько бы раз он не брал чёрный шарик, в его руках он всё равно слипается в один чёрный шарик. В третьей комнате каждый раз получался один чёрный шарик. Математическая запись: 0*n=0, где n - любое произвольное число, отличное от нуля. Почему отличное от нуля? Потому, что человек решил не брать чёрный шарик попозже и посмотреть, что из этого выйдет (Николай Хижняк: Смысл последней фразы я вообще не понял. «решил не брать попозже» - это как? Типа, «в будущем я такой ерундой вообще заниматься не буду»?).

Теперь человек решил взять 2 чёрных шарика в левой комнате, они снова слиплись в один. Затем он прошёл в комнату с цветными шариками и взял там два синих шарика (5). Произошло невероятное - чёрный шарик исчез. В его руках остались лишь 2 синих шарика. Войдя в третью комнату, в ней оказалось 2 синих шарика. Но можно и слепить эти 2 синих в один фиолетовый шарик – 10, но можно и оставить их в раздельном состоянии. Математическая запись: 0+5*2=10.

Тогда человек ещё раз вошёл в комнату с цветными шариками, на этот раз он взял один жёлтый шарик (3), 2 синих (5). И принёс их в третью комнату. Там он решил их совместить в один, получился один шарик бирюзового цвета 13. Математическая запись: 3+5*2=13.

Тут открылось интересное свойство цветных шариков, они, как и чёрные, могут слипаться в один шарик, но при этом изменяется их цвет, а значит и их числовое значение. Математическое выражение: n*b=y, где n, b, y – любое отличное от нуля число.

(Николай Хижняк: Главная проблема всех математиков, философов, физиков, на мой взгляд, - это неумение адекватно отражать различия между количеством и качеством математическими методами. Мы всё еще изучаем пещерную математику, которой нас научили наши предки. Собственных мыслей за последние столетия в математике не наблюдается вообще. Одни вариации на заданные темы, на затрагивающие самих основ математики. Все проблемные места математики очень аккуратно обходятся стороной. Но давайте посмотрим, что будет дальше с нашим экспериментом.)

Деление на ноль

Предисловие. Эту теорию деления на ноль написал Сергей Манулов. Свои комментарии к теории деления на ноль я буду писать в скобках. Если вы хотите высказать свое мнение о теории деления на ноль, можете сделать это в комментариях.


Ноль – очень противоречивое число (Николай Хижняк: Я уже давно говорю - уберите ноль из чисел и все проблемы с нулем в числовой области математики исчезнут). Известно со школьного возраста, что на ноль нельзя делить, иначе нарушается работа математического аппарата. Издревле софисты, деля на ноль, приводят доказательства того, что 2+2=5, 3=7 и тому подобное.

Деление на ноль вызывает неопределенность, поэтому математиками было решено запретить делить на ноль.

В теории пределов есть деление на ноль, но надо помнить, что с алгеброй это деление не связано, там свой смысл. И тот ноль, на самом деле - не ноль, а бесконечно малая величина. Но многие не вникают в подробности и потом утверждают, что при делении на ноль возникает бесконечность. На самом деле это не верно, так как ноль и бесконечно малая величина – совершено разные вещи. (Николай Хижняк: Выделено мною. Здесь я полностью согласен с Сергеем Мануловым. В теории пределов ноль выступает в роли горизонта, к которому стремятся бесконечно малые числа, никогда его не достигая. Впрочем, любое число так же может выступать в роли горизонта.)

Известно, что запреты существуют только для того, чтобы их нарушать. Поэтому, сейчас я попробую показать способ деления на ноль. Но сразу предупрежу, я строю собственные умозаключения на своих аксиомах, а не общепринятых. Поэтому, я начну с того, что дам определение математическим действиям, из которых буду строить логическое умозаключение, которое покажет вам, как можно делить на ноль. (Николай Хижняк: Хоть кто-то не боится пробовать математическую теорию на зуб. Посторонним людям это делать гораздо проще, чем самим математикам. На посторонних не оказывает давления бюрократическая система, созданная математиками.)

Определения:

Количество и разы в тексте являются синонимами по смыслу.

Сложение (прибавление) — одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае — два числа).

Умножение – это такое алгебраическое действие, в котором первый аргумент складывается столько раз, сколько показывает второй. В арифметике под умножением понимают краткую запись суммы одинаковых слагаемых. Например, запись 5*3 обозначает «сложить три раза пятёрку (три пятёрки)», то есть является просто краткой записью для 5+5+5.

Умножать можно только количество на количество, качество на количество, но никак качество на качество (Николай Хижняк: Последнее утверждение является явно ложным. Детский вопрос: сколько метров длины нужно сложить, чтобы получить один метр квадратный площади?). Пример: 2 лошади сильнее одной в 2 раза. Три раза взяли по два рубля, получили шесть рублей. Нельзя взять рубль по рублю раз (Николай Хижняк: Действительно, нельзя метр раз сложить один метр, но можно умножить метр на метр и получить метр квадратный; это доказательство того факта, что умножение принципиально отличается от сложения и сваливать их в одну кучу не правильно).

Нельзя складывать и умножать числа, обозначающие разные объекты, то есть нельзя складывать удава с попугаем, но если обозначить удава и попугая как животное, то можно получить сумму животных. Можно даже складывать утку и паровоз, если дать им общее между ними определение, такое, например, как "материальное тело" или "физический объект".

Пример: Было 2 утки, к ним прибавили 3 попугая и 4 паровоза. Сколько получилось:

а) Уток?
б) Попугаев?
в) Животных?
г) Физических тел?

Ответ:

а) 2
б) 3
в) 5
г) 9

(Николай Хижняк: А вот здесь предлагаю немного задержаться. Мой любимый детский сад. Детки уже всё понимают, но записывать ещё не научились. А как те, кто уже не одну диссертацию накатал? Они-то писать умеют? И так, в рассмотренном примере все ответы правильные, а мы их теперь возьмем и запишем:

а) 2+3+4=2
б) 2+3+4=3
в) 2+3+4=5
г) 2+3+4=9

Посмотрите, какая интересная математика получается! И ведь всё решено правильно. Зря мы деток в детском саду не заставляем записывать решения задачек. В чем прикол? В отсутствии единиц измерения. Без них вся математика превращается в бред. Именно этот бред мы начинаем изучать в школе и называем громким именем "математическая наука". Давайте запишем примеры ещё раз, но уже более подробно распишем логику своих рассуждений.

а) 2+3+4=2+3*0+4*0=2+0+0=2
б) 2+3+4=2*0+3+4*0=0+3+0=3
в) 2+3+4=2+3+4*0=2+3+0=5
г) 2+3+4=9

Вот теперь математическая запись решения стала гораздо ближе к правильному результату. Но и это не всё. На каком основании у нас появился ноль в качестве сомножителя? Вот мы такие умные, проанализировали условие задачи и расставили нули в нужных местах. Фигня всё это. Если называть вещи своими именами, мы просто подогнали решение под правильный результат. Как же выглядит решение на самом деле? Ноль - это один из управляющих элементов единицы измерения, вторым управляющим элементом является единица. Смотрите, как выглядит алгебраическая запись решений с управляющими элементами возле чисел при выполнении сложения.

а) 2+3+4=2*1+3*0+4*0=2+0+0=2
б) 2+3+4=2*0+3*1+4*0=0+4+0=3
в) 2+3+4=2*1+3*1+4*0=2+3+0=4
г) 2+3+4=2*1+3*1+4*1=2+3+4=9

И так, у нас имеются числа, отражающие количество единиц измерения, и управляющие элементы единиц измерения в виде нуля и единицы, через которые единицы измерения взаимодействуют с числами. Разные результаты получаются потому, что в каждом примере сложение выполняется относительно разных единиц измерения. Как известно всем из детского садика, и о чем всегда забывают математики, числа с одинаковыми единицами измерения складывать можно, с разными - нельзя.

На первый взгляд может показаться, что ноль и единица в нашем примере выступают в качестве элементов булевой алгебры. Да, булева алгебра занимается логикой и в ней только два элемента - ноль и единица. Логика полученных нами решений в разных вариантах задачи присутствует. Но... В основе булевой алгебры лежит теория множеств, а дальше по тексту у нас будет повод поговорить об этом динозавре математической науки. Теория множеств не отвечает на самый интересный вопрос - что лежит в основе формирования самих множеств? "Пусть нам дано множество..." - это вполне приемлемый аргумент для религии, но очень слабый для науки. В нашем случае набор нулей и единиц сформирован на основе единиц измерения. Как отображается относительность разных единиц измерения в разных случаях?

Здесь нам может помочь геометрия. Ведь известно, что сложение чисел можно изобразить при помощи сложения отрезков. Достаточно разобраться в геометрии разных способов сложения и мы получим геометрию единиц измерения. Но это довольно большая тема и рассматривать её нужно отдельно.)

Деление (операция деления) — одно из четырёх простейших арифметических действий, обратное умножению. Деление — это такая операция, в результате которой получается число (частное), которое при умножении на делитель даёт делимое.

Подобно тому, как умножение заменяет неоднократно повторенное сложение, деление заменяет неоднократно повторенное вычитание (Николай Хижняк: Справедливо для голых чисел, но полная ерунда для чисел с единицами измерения. Скорость - это деление длины на время. Как получить скорость из длины при помощи вычитания?).

Пример: 25/5=5, можно интерпретировать 3-мя способами:

а) У нас было качество 25, мы разделили его на 5 раз и получили качество 5. То есть, качество 25 состоит из 5 раз взятых качества 5.
б) У нас было качество 25, мы разделили его на 5 качеств, получили 5 раз.
в) У нас было 25 раз, мы разделили его на 5 раз и получили 5 раз. То есть, если взять 5 раз по 5 раз, получим 25 раз.

Разы нельзя делить на качество.

Итог: умножение состоит из складывания качества определенное число раз, либо из складывания разов определенное число раз. Математически это можно записать следующим образом: Р*К=К, Р*Р=Р, где Р - разы, К -качество.
Так как деление это операция обратная умножению, мы получим:

К/Р=К
К/К=Р
Р\Р=Р

Материя – это то, что существует, когда не существует пустота.

Пустота – это то, что не существует, когда существует материя.

0 (ноль или нуль) – число обозначающее:

а) как качество – пустоту
б) как количество – отсутствие объекта
в) точка отсчёта

Любое отличное от нуля число обозначает:

а) как качество – материю
б) как количество (разы) – наличие одного вида объекта определенное число раз.

Например: 3 будет обозначать, что объект присутствует 3 раза.

(Николай Хижняк: Продолжение статьи в следующей публикации. Главная ошибка всех рассуждений, как и у наших доблестных философов, это смешивание количества и качества в одну кучу. Философы даже закон специальный придумали о переходе количества в качество. Естественно, возникает вопрос вселенского масштаба - что такое "качество"?)

В Париже разрешили носить брюки

Величайшее достижение человечества - в Париже разрешили носить брюки. Женщинам. В ноябре 1799 года был принят закон, запрещающий парижанкам носить "мужскую одежду" без специального разрешения начальника полиции. В 1892 и 1909 годах законодатели смилостивились и разрешили парижанкам носить брюки во время верховой езды и езды на велосипедах. За появление на улицах Парижа в неподобающем виде женщину могли подвергнуть аресту. К частью, парижанам хватило ума не соблюдать этот дебильный закон. И вот, в 2013 году этот шедевр законотворчества был отменен.

На это можно было бы не обратить внимания, если бы не один момент. Вся человеческая история подтверждает, что в нашей жизни одни дураки законы пишут, другие дураки их выполняют. И вот представьте, что закон не отменили, а к власти во франции пришла очередная кучка идиотов. Они заставляют снимать брюки со всех женщин прямо на улицах Парижа. От мужиков, желающих помогать новой власти, отбоя не будет. Да и законопослушные дуры патлатые тоже найдутся. Гуманисты будут всех уверять, что новая власть поступает очень гуманно - ведь она не подвергают женщин аресту, как того требует закон, а просто позволяет законопослушным гражданам снимать с женщин недозволенную одежду, тем самым оберегая от совершения преступления последних. Вы не верите в подобный маразм? Я очень даже верю, путинская россия тому подтверждение.

Не далее, как десятки лет назад, очень цивилизованные и очень гуманные выродки убивали людей в газовых камерах концлагерей. Это были не инопланетяне, себя они называли высшей расой среди людей. Послушные бюрократические функции, которые тупо выполняли то, что им приказывали.

В это же время в другой стране другие выродки охотились на врагов народа, уничтожая сам народ. Спросите у своих бабушек и дедушек, как это было. Точно такие же бюрократические функции тупо выполняли распоряжения своего начальства.

Между фашистами и коммунистами разницы нет никакой. Первые предпочитают убивать чужих, вторые предпочитают убивать своих. Вот и все отличия. Бюрократические системы абсолютно одинаковы, как под копирку списаны из бюрократической системы инквизиции. Точнее, инквизиция переняла отшлифованную до блеска бюрократическую систему Древнего Рима. Разум на этой планете умер вместе с Архимедом от руки древнеримского воина. У этого тупого механизма для убийства даже не хватило ума взять ученого в плен и получить за это вознаграждение. С тех пор мы очень поумнели. Ученые фашисткой Германии и императорской Японии после окончания Второй Мировой войны тихонько перекочевали на работу в страны-победительницы. Хорошие и умные бюрократические функции нужны везде.

Вся структура любой бюрократической системы построена на математических принципах. Неравенство - вот математическая основа бюрократии. Как мы не можем представить себе равенство чисел, так же мы не можем представить равенство среди людей. Если есть люди, значит они должны быть объединены в бюрократическую систему: религиозную, государственную, политическую, коммерческую, научную... Сами системы так же стремятся выстроить бюрократическую иерархию среди себе подобных. Во всех странах идет постоянное соперничество между разведкой и контрразведкой, между органами внутренних дел и органами государственной безопасности, между математиками и физиками, между христианами и мусульманами...

Маразм любой бюрократической системы определяется уровнем маразма составляющих её бюрократических функций. Если бы во Франции за поимку парижанки в штанах объявили денежное вознаграждение, мы бы с вами увидели совсем другой Париж - со снятыми штанами и с целой кучей голодных шавок без намордников, высматривающих добычу. Некоторые исламские страны демонстрируют нам примеры тупого следования законам шариата. В странах, называющих себя демократическими, дела обстоят не лучше. Антикоммунизм, доведенный до маразма в послевоенных Соединенных Штатах Америки, преследовал самые гуманные цели и опирался на принятые в стране законы.

Системы образования всех стран готовят послушных исполнителей, пригодных для работы в любых бюрократических системах. В идеале любой сотрудник должен "угадывать мысли и будущие действия руководителя и действовать в соответствии с ними". Это цитата из наставления для секретарш. Но это же и мечта любого руководителя из любой бюрократической системы. Очень многие математические задачки не учат понимать математику, а учат угадывать мысли составителей задач. И это очень грустно.

Диагонали прямоугольного параллелепипеда

Вопрос, конечно, интересный задали: как найти объем прямоугольного параллелепипеда, зная три его диагонали, выходящие из одной вершины? Первая мысль - порыться в математическом справочнике. Но мой любимый справочник молчит. Есть другой кладезь мудрости - Википедия. Русскоязычная страница, посвященная прямоугольному параллелепипеду, поражает своим убожеством. Даже теоремы Пифагора для трехмерного пространства там нет. Обычно в таких случаях я перехожу на точно такую же страницу на английском языке. Ведь математика - это такая штука, которая в переводчиках не нуждается. Чаще всего там гораздо больше разных формул. В этот раз меня ждало великое разочарование. Да, я увидел там теорему Пифагора для прямоугольного параллелепипеда. И всё. Всякой математической фигни в Википедии навалом, а вот самого нужного в данный момент нет. Печалька.

Попробуем рассуждать логически. Если кому-то задали такую задачу, значит решение этой задачи есть. Наши математики ещё не доросли до того уровня, когда признаются своим ученикам в своем незнании чего-то. Разве что самые смелые. Остальные тупо повторяют то, чему учили когда-то их. Само собой напрашивается решение: составляем теоремы Пифагора для трех диагоналей граней, объединяем их в систему трех уравнений с тремя неизвестными, решаем и находим размеры прямоугольного параллелепипеда. Брррр! Ужас.

Теперь порассуждаем с другой стороны. Объем - это результат умножения трех измерений длины. У нас есть три длины диагоналей. Теоретически, из них можно получить объем. Давайте нарисуем наши диагонали прямоугольного параллелепипеда и посмотрим, что можно с ними сделать. Смотрим с разных сторон, чтоб понятнее было.

Диагонали граней прямоугольного параллелепипеда

На картинке синим цветом выделены те элементы прямоугольного параллелепипеда, которые нам известны. Это диагонали граней. Красным цветом выделено то, что нам не известно. Это диагональ прямоугольного параллелепипеда и его линейные размеры (математики любят еще называть их измерениями параллелепипеда). Ну, и сам объем нам тоже не известен.

Теперь вооружимся древней теоремой дедушки Пифагора и запишем формулы размеров и диагоналей. Параллелепипед у нас прямоугольный, значит все углы между линейными размерами и гранями прямые. Не забываем также, что наша главная цель - найти объем.

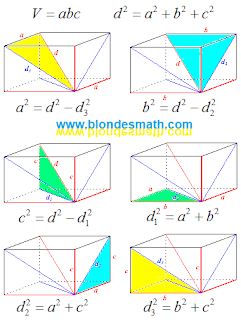Ребра и диагонали прямоугольного параллелепипеда

Картинки несколько отвлекают от формул. Выписываем формулы отдельной кучкой. Математики в это случае с умным видом бы изрекли: "математическое множество формул". Смотрим на формулы и пытаемся хоть что-то соображать. Нам нужно избавиться от измерений и диагонали прямоугольного параллелепипеда, ведь они нам не известны. Вот если бы диагональ параллелепипеда выразить через диагонали боковых граней... Уж очень формулы в правой половине кучки похожи друг на друга.

Диагонали прямоугольного параллелепипеда формулы

Есть! Квадраты диагоналей граней равны двум квадратам диагонали параллелепипеда. Теперь совсем просто. Как кубики в детском садике. Скобочки убираем, скобочки добавляем... И получаем формулу.

Диагонали прямоугольного параллелепипеда преобразования

После этого полученную формулу подставляем в формулы с линейными размерами и получаем выражение линейных размеров через диагонали граней. Потом записываем формулу объема.

Диагонали прямоугольного параллелепипеда и объём

Всё. Задача решена. Получилась очень красивая и изящная формула. Из суммы квадратов двух диагоналей граней вычитается квадрат третьей грани. Потом это перемножается, делится на восемь и получается квадрат объема прямоугольного параллелепипеда. Насколько понимаю я, это одно из основных свойств пространства. Используя принцип перегруппировки сомножителей и слагаемых, можно выводить подобные формулы для многомерных пространств с любым количеством измерений. Любой многомерный объем можно выразить через элементы с меньшим количеством измерений. К сожалению, нам математики об этом ничего не рассказывают. То ли сами ничего не знают, то ли стесняются. А ведь перед нами красота математики в первозданном виде, лишенная всяких заморочек, которые так любят наши учителя.