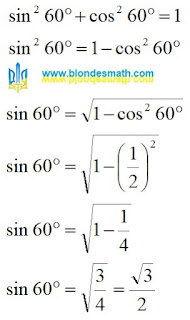Отрицательные числа: игра в числа

Вы все видели игру в шахматы. Взрослые люди выходят на сцену, садятся за стол друг напротив друга и начинают игру.

Давайте организуем подобную игру между математиками. Назовем её "Игра в числа". Правило очень простое – побеждает тот математик, который правильно нарисует числовую ось.

Два математика выходят на сцену, садятся за стол напротив друг друга. Между игроками находится лист бумаги. На листе уже нарисована ОДНА прямая линия. Задача игроков — превратить эту линию в числовую ось. Звучит гонг, игра началась.

Игроки рисуют ноль, помещают стрелку в направлении положительных чисел и выбирают размер одной единицы. После этого на игровом поле появляются положительные и отрицательные числа. Игра закончена.

Отрицательные числа: игра в числа

Как и следовало ожидать, игра завершилась вничью. Оба математика правильно нарисовали числовые оси. В полном соответствии с определениями, как их учили. Дальше победителя можно определить либо по количеству научных публикаций, либо переходом от математики к боксерскому поединку.

Что мы получили в результате этой "Игры в числа"? Все числа оказались одновременно и положительные, и отрицательные. Знак числа зависит от того, с какой стороны мы смотрим на числовую ось. Ведь положительные числа всегда расположены справа от нуля, а отрицательные - слева.

Секрет этого фокуса заключается в том, что в природе числа не имеют знака. Знаки плюс и минус являются отражением нашего собственного мнения о том или ином числе. Это мнение может быть разным у двух разных людей.

Отрицательные числа: это долг

Автор Николай Хижняк

Нельзя отнять жизнь у мертвого.

В одном из научно-популярных фильмов математика приводит пример с отрицательными числами: «У вас есть минус одна рыба. Вы пошли на рыбалку, поймали одну рыбу и у вас ничего не осталось. Удивительный результат!».

Математическая запись этой истории выглядит так:

-1 + 1 = 0

Теперь предположим, что я рыбак. Вот как я вижу эту историю. Кто-то говорит, что у меня минус одна рыбина. Фактически же у меня ничего нет. Как я это могу записать? Я пишу ноль.

0

Я иду на рыбалку, мне удалось поймать одну рыбу. Теперь у меня есть одна рыба. Я прибавляю единицу.

0 + 1 = 1

После этого появляется тот, кто утверждал, что у меня минус одна рыба, и забирает мою рыбу себе. Прям как россияне в Украине.

0 + 1 - 1 = 0

Упс! Где здесь отрицательные числа? Это самый заурядный рэкет - "русский мир" пришел в мой дом.

Теперь давайте посмотрим, что значит взять в долг. Мне срочно нужны деньги, 1 доллар. Что у меня есть сейчас? Ничего, ноль.

0

Хороший человек (или злой банк) дал мне 1 доллар. Что у меня есть сейчас? У меня есть реальный положительный 1 доллар, который я могу потратить, как захочу. Но нет, я не буду тратить его зря. Я сохраню его как музейный экспонат.

0 + 1 = 1

Через некоторое время я заработал 1 доллар. Сколько у меня денег?

1 + 1 = 2

Я честный человек и оплачиваю свои долги. Сколько денег у меня останется?

2 - 1 = 1

Я одолжил деньги, вернул их, и у меня остался 1 доллар. Или у меня останется то, что я купил. Что это было? Были ли это отрицательные числа? Нет. Это была машина времени, позволяющая мне сегодня купить то, на что я смогу заработать только завтра.

Главное правило такое: нельзя взять в долг то, чего нет. Попробуйте взять в долг машину времени, вечный двигатель или летающую тарелку. Это невозможно сделать, потому что этих вещей для нас не существует. И сколько бы минусов мы не обещали, все равно этих вещей мы не получим. Нельзя отнять жизнь у мертвого.

Дальше я предлагаю провести соревнования по игре в числа.

Таблица простых чисел

Простые числа - это натуральные числа, которые делятся только на единицу и сами на себя. Простые числа играют видную роль в теории чисел. Основная теорема арифметики говорит о том, что любое целое число больше единицы либо является простым, либо его можно представить в виде произведения простых чисел. Спорить с содержанием этой теоремы не вижу оснований, а вот к названию лично у меня очень большой вопрос. Если это "основная теорема" арифметики, то у меня закрадываются подозрения, что начало учебника по арифметике наши математики выкурили в виде самокруток ещё в дошкольном возрасте, а в школе начали изучать то, что осталось.

Ниже представлена таблица простых чисел от 2 до 20000. Эта таблица простых чисел может вам пригодиться при сокращении дробей.

Таблица простых чисел от 2 до 1000

Таблица простых чисел от 1000 до 10000

Таблица простых чисел от 10000 до 15000

Таблица простых чисел от 15000 до 20000

Простые числа — любимая игрушка математиков. По состоянию на январь 2019 года самое большое простое число, известное математикам, имело 24 862 048 десятичных цифр. Эта игра с простыми числами настолько увлекательна, что даже я пристрастился к этой игре. Что я могу сказать по этому поводу? Игра в простые числа очень трудоемка и утомительна, но результаты могут быть очень интересными. Я придумал свои правила игры, о которых скоро вам расскажу. Надеюсь, это будет интересно математикам.

Сперва мне понадобились простые числа до 20 000. Я добавил эти таблицы сюда. Потом мне нужны были простые числа до 1 000 000. Потом я плюнул на это грязное дело потому, что мне надоело. Если вам вдруг понадобится, то здесь вы найдете простые числа до 21 000 000.

Каковы результаты моих "научных" изысканий? Ничего интересного, результат оказался всем давно известным - чем дальше в лес, тем больше дров по числовой прямой от нуля, тем реже встречаются простые числа. Разве что на ноль мне удалось взглянуть с неожиданной стороны. Всё красиво оформлю и поделюсь с вами.

Отрицательные числа: вычитание

Математики рассказывают нам о положительных и отрицательных числах. Только после этого они говорят об абсолютном значении числа (модуле числа). Я не доверяю математикам. Я считаю, что в природе всё обстоит с точность до наоборот - есть только числа с их абсолютными значениями, а уже потом к этим числам мы можем добавить знак "плюс" или "минус.

Существуют ли в природе отрицательные числа? Что означают знаки плюс и минус в математике? Мы попробуем разобраться в этом.

Математики говорят, что отрицательные числа появляются в арифметике при вычитании, когда из меньшего числа вычитается большее число. Меня тоже так учили.

Если мы всегда будем вычитать из большего числа меньшее число, тогда отрицательные числа никогда не возникнут. Это правило ничем не лучше и не хуже того правила, которому нас учат математики. Вы можете себе представить математику без отрицательных чисел? Математикам такое даже в страшном сне не приснится. А вот что получается на самом деле.

Вычитание

Минусы отвалились, как засохшая грязь. Остается кристально чистое сложение положительных чисел. Этот пример наглядно показывает, что отрицательные числа нельзя получить при помощи вычитания.

Я все сделал правильно. Меня так учили в школе. Если минус x равно минус единице, то x равно единице.

-х = -1

х = 1

В чем секрет этого фокуса? Математики неправильно решают задачу на вычитание. Если нам известен результат сложения и одно из слагаемых, то второе слагаемое мы можем найти при помощи вычитания. Для этого из известной нам суммы нужно вычесть известное нам слагаемое. А сумма всегда больше, чем любое из слагаемых. Если мы из слагаемого вычтем сумму, тогда знак минус нам укажет на то, что мы запутались.

Давайте посмотрим, как выглядят мои преобразования выражения на числовой оси.

Вычитание на числовой оси

В левой части рисунка показана неподвижная числовая ось. Ноль числовой оси остается на месте, отрезки, как блохи, скачут около нуля. В правой части рисунка отрезки неподвижны, а числовая ось мечется вдоль них. Ноль перемещается в пределах отрезков. При этом во всех случаях знак числа меняется при переходе через ноль. В алгебре это равносильно перемещению числа через знак равенства - знак числа меняется на противоположный. В дальнейшем мы ещё вернемся к числовой оси с целью более внимательного её рассмотрения. Знак равенства и ноль - это математическая граница, при пересечении которой шпионы становятся разведчиками, а разведчики - шпионами.

С вычитанием мы разобрались. Никакие отрицательные числа при вычитании не возникают. Дальше мы посмотрим, возникают ли отрицательные числа, если мы берем в долг.

Синус и косинус таблица

Лига лени: Оно вам надо?

Это самая необычная таблица синусов и косинусов. Идея сделать такую таблицу пришла ко мне в процессе написания этих статей:

Почему синус 30 градусов равен одной второй?

Чему равен синус 60 градусов?

Синус и косинус 45 градусов

Я настоятельно рекомендую вам прочитать эти статьи. Тогда вы узнаете, как легко вычислить значения синуса и косинуса самостоятельно. Из этих трех статей я сделал одну таблицу синусов и косинусов.

Синус и косинус таблица

Теперь разбор полетов моей фантазии. Есть много разных способов запомнить значения синуса и косинуса основных углов. Предлагаемый мною способ для тех, кто любит считать. Прежде всего, нужно хорошо запомнить, что косинус - это в сторону, по оси икс. Синус - это вверх, по оси игрек. Дальше изучаем таблицу.

В таблице показано, какие стороны треугольника нужно принять за единицу, чтобы было проще считать. Для 0 и 90 градусов треугольников не существует, это обычные отрезки. Значения синуса и косинуса для этих углов равны либо нулю, либо единице. Всё зависит от положения отрезка - либо вверх, либо в сторону.

Третий столбец таблицы показывает, как использовать теорему Пифагора для вычисления нужного значения синуса или косинуса. Для косинуса 30 градусов и синуса 60 градусов вычисления одинаковы. Для косинуса 45 градусов и синуса 45 градусов вычисление другое. Всё разнообразие таблицы сводится к наглядным картинкам и двум разным вычислениям, которые не трудно запомнить.

Внизу таблицы есть подсказки, как вычислить значения тангенса и котангенса, если вы знаете значения синуса и косинуса. Если вы забыли, как делить одну дробь на другую, воспользуйтесь еще одной подсказкой. Вам нужно умножить первую дробь на обратную вторую дробь.

Синус и косинус 45 градусов

Лига лени: синус 45 градусов равен корень из двух, деленный на два. Картинки смотреть? А зачем?

Наша экспедиция в прошлое помогла нам узнать, почему синус 30 градусов равен одной второй и чему равен синус 60 градусов. Теперь пришло время разобраться с синусом и косинусом 45 градусов.

Если вы были внимательны во время путешествия в прошлое, вы не могли не заметить квадрат, разделенный на две части диагональю. Одна половинка такого квадрата даст нам прямоугольный равнобедренный треугольник. Это очень редкий зверь в стаде треугольников. Математикам он известен уже много тысяч лет и математикам просто скучно возиться с ним.

Прямоугольный равнобедренный треугольник

Да, это уставший треугольник. Он лег на бочок отдыхать. Ну не вечно же равнобедренный треугольник должен стоять на основании, как пирамида Хеопса.

Прямоугольный равнобедренный треугольник

Катеты этого треугольника равны единице (я так хочу). Еще раз повторяю, что оба катета имеют одинаковую длину. Нам неизвестна длина гипотенузы этого треугольника, но мы можем легко вычислить ее по теореме дедушки Пифагора, с которым мы мило беседовали во время нашей экспедиции в прошлое.

Синус и косинус 45 градусов

Как сказал какой-то знахарь математики, синус и косинус угла равны отношению катета к гипотенузе. Поскольку катеты прямоугольного треугольника с углом 45 градусов равны, то значение синуса 45 градусов равно значению косинуса 45 градусов. Берем математику в руки и вычисляем это значение.

Синус и косинус 45 градусов

Почему я умножил числитель и знаменатель дроби на квадратный корень из двух? Маленькие дети не любят комочков в каше. Математики не любят квадратные корни в знаменателях. Очень капризные дяди и тёти.

Чему равен синус 60 градусов?

Лига лени: синус 60 градусов равен корень из трех, деленный на два. Картинки можете не смотреть.

В поисках ответа на вопрос "Почему синус 30 градусов равен одной второй?" мы использовали машину времени. Если кто-то ещё не вылез из этой машины - просьба покинуть аппарат. Больше он нам не понадобится. Теперь мы будем разбирать те материалы, которы были собраны во время экспедиции в прошлое. Сегодня рассмотрим вопрос "Чему равен синус 60 градусов?".

Высота равностороннего треугольника

Берем равносторонний треугольник со стороной, равной единице, и с проведенной через вершину треугольника высотой. Этот рисунок мы рассматривали прошлый раз.

Высота равностороннего треугольника

В этот раз мы не будем поворачивать рисунок, а просто уберем его половину - один из двух прямоугольных треугольников.

Косинус 60 градусов.

Где-то там, в глубине веков, какой-то знахарь математики нам громко кричал про синус и нашептал о косинусе. Шепот гласил, что косинус угла - это отношение прилежащего катета к гипотенузе прямоугольного треугольника. Нас интересует угол в 60 градусов.

Косинус 60 градусов

Прилежащий к углу в 60 градусов катет расположен горизонтально внизу прямоугольного треугольника. Длина этого катета равна одной второй. Гипотенуза этого треугольника равна единице. При делении на единицу число не меняется. Вот и получается, что в этом треугольнике длина прилежащего катета равна косинусу 60 градусов, а значит косинус 60 градусов равен 1/2.

Синус 60 градусов.

Высота этого прямоугольного треугольника будет равна синусу 60 градусов. Как найти высоту прямоугольного треугольника? У нас есть старая добрая теорема Пифагора. Вот её и используем.

Синус 60 градусов

После не сложных вычислений у нас получилось, что синус 60 градусов равен корню квадратному из трех, деленному на два. Прошу заметить, что вычисления для синуса 60 градусов точно такие, как для косинуса 30 градусов. Такова наша математика.

Почему синус 30 градусов равен одной второй?

Лига лени: просто смотрим картинки.

Самый простой ответ на вопрос "Почему синус 30 градусов равен одной второй?" будет звучать следующим образом: так исторически сложилось. Ничего не понятно? Согласен. Нужно глубоко вникать в кучу других интересных вопросов, типа: "Почему прямой угол равен 90 градусов?", "Почему синус мы считаем так, а не иначе?"и так далее. Но есть и другой, более наглядный ответ, если не вникать во всякие "Почему?".

Для этого выбрасываем всякую математическую дрянь из головы, садимся в машину времени и отправляемся на несколько тысяч лет назад, в прошлое. Древний Вавилон. Оказывается, местные аборигены о математике знают гораздо больше, чем о ней помнит среднестатистический наш современник. Корень из двух они легко подглядывают в своей глиняной математической шпаргалке. Какие счастливые люди здесь живут - о тригонометрии ничего не слышали! А это что такое? Так, так, так, учили в школе, знаем.

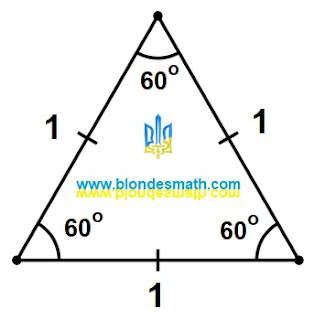
Равносторонний треугольник

Равносторонний треугольник

Перед нами равносторонний треугольник со стороной, равной единице. Все углы этого треугольника равны 60 градусов. Напомню, что в Древней Месопотамии (а Вавилон располагался именно там) была принята шестидесятеричная система счисления, которую мы с успехом используем сегодня для измерения углов и времени - 60 минут, 60 секунд. Так что для Древней Месопотамии равносторонний треугольник, с его углами в 60 градусов, был очень даже патриотичным.

Мы не станем отправляться в экспедицию по Древней Месопотамии в поисках других местных знаний о треугольниках. Сомневаюсь, что в те древние времена к любопытным чужеземцам относились иначе, чем сейчас. Лучше отправимся в Древнюю Грецию. Уж там точно знали толк в треугольниках.

Высота равностороннего треугольника

Высота равностороннего треугольника

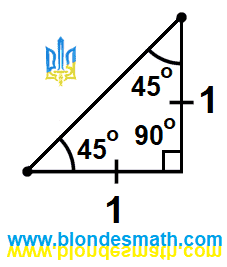
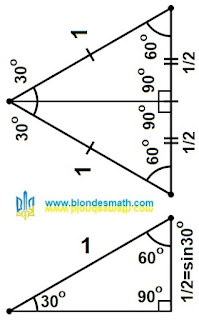
Думаю, что древнегреческие математики уже хорошо знали, что высота равнобедренного треугольника делит его на два одинаковых прямоугольных треугольника. Что высота треугольника всегда перпендикулярна его основанию. Высота разделила угол в 60 градусов в вершине треугольника на два угла по 30 градусов. Основание, равное единице, эта высота так же разделила поровну - 1/2 и 1/2. Очень демократичная дележка треугольника у основателей демократии получилась. И хотя о самих тригонометрических функциях древнегреческие математики ничего не знали, геометрические и вычислительные основы в фундамент тригонометрии они заложили.

Синус 30 градусов

Проходят тысячелетия и тут появляется какой-то знахарь математики и сообщает нам радостную ну такую себе весть: "Я придумал тригонометрические функции!!! Синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе! (Дальше шёпотом) А вот косинус угла равен отношению прилежащего угла к гипотенузе." Упс... И что нам теперь с этим делать? Остается только терпеть и попытаться разобраться во всей этой математической ерунде. Начинаем соображать. Прямоугольный треугольник мы знаем... В углах треугольника мы тоже кое-что понимаем... Вау! Да это же элементарно! Как найти значение синуса для угла 30 градусов? Я просто переворачиваю картинку на 90 градусов и удаляю всё лишнее.

Синус 30 градусов

И так, ещё раз: синус угла - это отношение длины противолежащего катета к длине гипотенузы. В нашем прямоугольном треугольнике длина гипотенузы равна единице. При делении любого числа на единицу, это число не меняется. Следовательно, длина противолежащего катета, равная 1/2, является значением синуса угла в 30 градусов. Как любят говорить математики: "Что и требовалось доказать".

Косинус 30 градусов

Косинус 30 градусов можно легко найти по теореме дедушки Пифагора, ведь треугольник у нас прямоугольный и применять этот математический шедевр мы имеем полное право. Берем в руки математику и считаем.

Косинус 30 градусов

После вычислений у нас получилось, что косинус 30 градусов равен корню квадратному из трех, деленному на два.

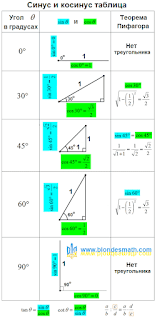
Вот как легко всё вычисляется, даже таблицы не нужны.