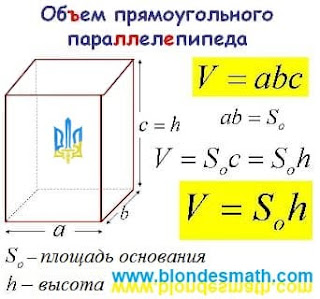
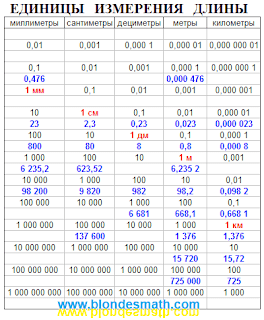
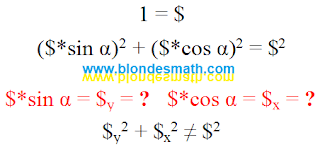Здесь мы не будем рассматривать доказательство теоремы Пифагора. Доказательств много и вы их без труда найдете. Сегодня мы рассмотрим преобразование теоремы Пифагора из тригонометрического вида в другие виды с применением различных единиц измерения. Такие исследования математических свойств разных
единиц измерения должны быть неотъемлемой частью
математики. К сожалению, никто нас этому не учат. Но если вы хотите понимать математику, вы должны это знать.
Прежде всего, отметим те существенные моменты, которые влияют на применение теоремы Пифагора к окружающей действительности:
1. Две единицы измерения должны быть перпендикулярны.
2. Перпендикулярные единицы измерения должны быть одинаковыми (P.S. 26.03.23г. Не обязательно, единицы измерения могут быть разные).
Если две перпендикулярные единицы измерения будут разными, мы не сможем выполнить их сложение (
P.S. 26.03.23г. Сможем. Главное, чтобы единицы измерения слагаемых были одинаковыми). Таковы правила сложения, которым нас учат в самом раннем возрасте и которые потом нас учат напрочь забывать. По умолчанию принято считать, что если между числами мы поставили знак плюс или минус, то эти числа имеют одинаковые единицы измерения. Весь окружающий мир не превращается в бесформенную серую массу потому, что даже одно число может иметь бесконечное множество единиц измерения. Именно единицы измерения удерживают разные величины от сложения в одно целое.
Тригонометрическая форма теоремы Пифагора, которую мы называем
основным тригонометрическим тождеством, является формой записи теоремы Пифагора
без единиц измерения. Это один из основных математических законов, который при введении разных единиц измерения превращается в разные физические законы.
Произведем преобразования основного тригонометрического тождества так, что бы мы могли потом подставлять любые единицы измерения и получать результат. Для этого введем нейтральные элементы в эту формулу.
 |
| Теорема Пифагора |
Почему единица возведена в квадрат? Потому, что в математике так писать не принято, но это объясняет смысл того, что будет происходить дальше. Теперь мы приравниваем нашу единицу к длине гипотенузы прямоугольного треугольника и получаем теорему Пифагора в классическом виде - сумма квадратов катетов равна квадрату гипотенузы.
 |
Теорема Пифагора для треугольника
|
Заметьте, не имеет значения, что мы будем называть синусом, а что косинусом. Не имеет значения, какой из двух острых углов мы возьмем - теорема Пифагора работает
для двух этих углов одинаково. Главным является то, что сумма квадратов отношений гипотенузы к катетам равна квадрату самой гипотенузы, всё остальное - это проявления относительности
тригонометрических функций. Теорему Пифагора можно рассматривать как математическое доказательство
переместительного закона (математики называют это коммутативностью) сложения - от перестановки слагаемых сумма не меняется. Коммутативность - ещё одно проявление относительности в математике.
Теперь посмотрим, что получится, если вместо единицы мы подставим радиус окружности.
 |
| Теорема Пифагора для окружности |
Получается, что сумма квадратов
координат точек окружности равна квадрату радиуса. Но, не нужно при этом забывать главное условие -
центр окружности должен совпадать с центром декартовой системы координат. Если центр окружности и центр системы координат не совпадают, тогда это утверждение рассыпается, как карточный домик. Окружность и декартовы координаты - это две абсолютно независимые системы, которые могут располагаться, как угодно. Кто сказал, что центр окружности
всегда должен совпадать с центром системы координат? Математики? Они пошутили.
Нужно обратить внимание ещё на один момент - знаки чисел. Теорема Пифагора их полностью игнорирует даже при наложении на окружность декартовой системы координат в классическом виде - с положительными и отрицательными направлениями. Возведение любого числа в квадрат полностью лишает это число знаковых признаков. Это свидетельствует о том, что
в математике главным является само число, а не тот знак, который мы этому числу приписываем.
Дальше мы подставим вместо единицы длину отрезка.
 |
Теорема Пифагора для отрезка
|
У нас получилось, что сумма квадратов проекций отрезка на оси
прямоугольной системы координат равна квадрату длины отрезка. Я не зря подчеркнул, что система координат должна быть прямоугольной. Для косоугольной (аффинной) системы координат теорема Пифагора будет выглядеть по-другому. Взаимное положение отрезка и системы координат значения не имеет. Так же не имеет никакого значения, есть в системе координат отрицательные направления или нет. Проективные свойства пространства проявляются уже в момент возникновения самого пространства, до того, как в этом пространстве появляемся мы со своими знаками чисел. Кстати, в момент появления пространства возникает и симметрия, которая заставляет нас применять отрицательные числа, что бы мы могли различать симметричные явления. Есть ли у инопланетян отрицательные числа? Понятия не имею. Но знаю точно, что у них обязательно есть что-то, что помогает им адекватно отображать свое отношение к симметрии. Поэтому, когда встретитесь с ними, не сильно удивляйтесь, что они не понимают ваших рассказов о плюсах и минусах.
Теперь подведем маленький итог. Всё то, что мы с вами рассмотрели - гипотенуза треугольника, радиус окружности, отрезок - это различные названия одной и той же
единицы измерения длины. Все перечисленные геометрические объекты измеряются в сантиметрах, метрах, километрах и так далее. Просто в разных ситуациях нас научили называть длину по-разному. В повседневной жизни это удобно, в математических операциях эти различия в названиях не имеют никакого значения, вы
всегда имеете дело с длиной. Все рассмотренные нами разновидности теоремы Пифагора - это различные варианты записи одного и того же
математического закона для двух перпендикулярных измерений длины.
В качестве следующей единицы измерения возьмем единицу измерения времени. Для времени теорема Пифагора будет выглядеть так:
 |
Теорема Пифагора и время
|
Сумма квадратов
проекций времени на перпендикулярные направления равна квадрату самого
времени. Естественно, здесь возникает целый ряд вопросов.
Существуют ли у времени перпендикулярные направления? Мы этого не знаем, но это совсем не означает, что у времени не может быть перпендикулярных направлений. Точно нам смогут ответить только физики. Думаю, на ближайшее тысячелетие им работы хватит.
Сколько измерений имеет время? Некоторые уверены, что одно. Некоторые высказывают предположение, что больше. Лично я рассуждаю так. У длины имеется минимум три пространственных измерения, в которых мы живем - длина, ширина, высота.
У времени должно быть такое же количество измерений, как и у длины, иначе нарушаются основные математические принципы - симметрии и относительности.
Можно ли применить теорему Пифагора для времени? Да, можно. Совсем скоро я вам покажу то место, где разложение времени по теореме Пифагора будет смотреться очень естественно и логично.
Дальше рассмотрим другие единицы измерения. Для примера возьмем единицы измерения температуры и единицы измерения денег. Это точно такие же математические объекты, как и длина, но приметить теорему Пифагора к ним не возможно - эти единицы измерения не имеют точно таких же перпендикулярных единиц измерения. Посмотрите, что получается для температуры.
 |
Теорема Пифагора и температура
|
И для денег. В качестве примера единиц измерения денег возьмем доллар.
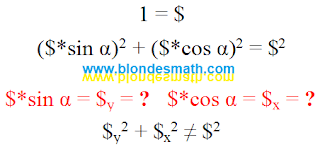 |
Теорема Пифагора и доллар
|
Точно такая же картина вырисовывается, если мы будем пробовать подставлять в теорему Пифагора все другие, известные нам, единицы измерения. К ним теорема Пифагора не применима из-за отсутствия перпендикуляра у каждой из них. Следовательно, все эти единицы измерения обладают несколько иными математическими свойствами, чем длина и время - к ним нельзя применить тригонометрические зависимости, в том числе и теорему Пифагора.
В завершение наших исследований рассмотрим обратный процесс - превращение теоремы Пифагора для прямоугольного треугольника в основное тригонометрическое тождество. Для этого разделим все элементы математического выражения на квадрат длины гипотенузы и выполним преобразования.
 |
Теорема Пифагора и тригонометрическое тождество
|
Мы снова вернулись к тригонометрической форме теоремы Пифагора, с которой мы начинали.
В заключение хочу признаться, что совсем недавно я встречался с инопланетянами. Так вот, в процессе общения они нарисовали мне довольно странный рисунок. Вот он.
 |
Теорема Пифагора для инопланетян
|
Что инопланетяне хотели этим сказать? Что они умеют рисовать палочки и кружочки? Как-то примитивно для них. Наверное, что-то другое. Инопланетяне умнее меня, ведь это они прилетели ко мне в гости, а не я к ним. Может быть, так выглядит их планета в
комплексом пространстве двенадцати переменных? Знаете, наша планета в трех реальных измерениях длины выглядит гораздо красивее.