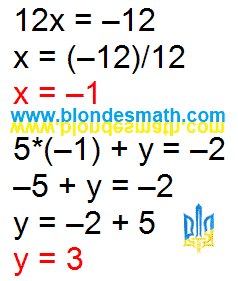Простое решение системы уравнений

Перед нами неразрешимой задачей громоздится система уравнений. Хочу сразу сказать, что нам предстоит рассмотреть простое решение системы уравнений, которая кажется очень трудной. В чем проблема? В одних скобочках есть икс и игрек, во вторых скобочках есть только икс, а игрек напрочь отсутствует. Как решать такую систему? Катастрофа! Если вы думаете именно так, то у вас начинает развиваться синдром математика: вы не понимаете, как такому взрослому человеку, как вы, могут задавать такие детские задачки. Здесь явно какой-то подвох. И вы начинаете его упорно искать.

А подвоха никакого нет. Все решается действительно просто. Я для решения применю метод разложения одной системы уравнений на две. Не пытайтесь искать этот метод в учебнике математики - это я только что придумал сам. Вам придется мое решение оформить так, как вас учили. Или придется сказать преподавателю математики: "Так решает лысый дядька из Интернета...". Понятно, что ни "лысый дядька", ни "лысая тётка" учебниками математики не являются. А Интернет - это просто большая шпаргалка, в которой очень много всякой ерунды.

И так, с умным видом смотрим на нашу систему уравнений и начинаем рассуждать. В первом уравнении у нас две штучки умножаются и дают в итоге ноль. Когда такое бывает? Вспоминаем детские правила умножения. Правильно, когда одна из этих штучек равняется нулю - первая или вторая. Вот я и разложу первое уравнение на два, приравняв к нулю каждое выражение в скобках. Внизу дописываю второе уравнение из заданной нам системы и получаю две системы уравнений с двумя неизвестными. Объединяются эти две системы уравнений в одно целое нижним уравнением, которое является общим. На этом основании мы можем рассматривать решение каждой системы как одно из решений исходных уравнений. Согласитесь, каждая из этих систем выглядит уже не так страшно, как первоначальная.

Простое решение системы уравнений

Каждую систему я буду решать отдельно, применяя описанные в учебнике математики методы. Первую систему решаем методом сложения, точнее, вычитания. Если к первому уравнению прибавить второе уравнение со знаком минус, мы получим вычитание уравнений. Вычитание я запишу не поэлементно (иксы, игреки, числа), а в столбик, что не меняет смысл выполняемых при этом действий. Кстати, в высшей математике это простое действие будет обзываться очень умными словами: "матричный способ вычитания вектор-строк". Но вернемся к первой системе уравнений. Из первого уравнения вычитаем второе и сразу получаем значение игрека. Подставляем полученное значение в одно из уравнений и находим значение икса. Я подставил во второе. При подстановке в первое уравнение мы получим точно такой же результат.

Простое решение системы уравнений

Вторую систему решаем методом подстановки. Из первого, детского, уравнения находим значение икс и подставляем во второе уравнение. Так мы найдем значение игрек.

Простое решение системы уравнений

Решением исходной системы уравнений будут две пары значений иксов и игреков. Для того, чтобы в этом убедиться, выполняем мою любимую проверку. После подстановки двух пар неизвестных в заданную систему мы получаем правильный результат. Значит, эта простая система уравнений решена правильно. Я надеюсь:)

Простое решение системы уравнений

Как-то так.

Как запомнить значения тригонометрических функций

При подготовке к экзаменам или ЕГЭ вам может понадобиться вызубрить таблицу значений тригонометрических функций. Возникает вопрос: как запомнить значения тригонометрических функций? Могу вас обрадовать - особо сильно зубрить ничего не нужно. Есть довольно простой, механический способ получить значения тригонометрических функций для самых распространенных углов. Это углы в 0, 30, 45, 60 и 90 градусов. Для других углов математики сами редко что помнят - зачем забивать голову всякой ерундой, когда есть справочники, таблицы и калькуляторы?

Способ очень простой. Берете чистый листик бумаги. На нем записываете числа 0, 1, 2, 3, 4. На эти числа одеваете шапочку квадратного корня. Затем весь этот пионерский отряд в шапочках делите на число 2. У вас получились детские примерчики, которые вам нужно решить. Если вы дожили до тригонометрических функций, то такие примеры вы должны щелкать, как орехи, не прилагая особых умственных усилий. Напоминаю, что корень из нуля равен нулю, корень из единицы равен единице. Чему равны корни из двух и трех ни вы, ни я не помним, поэтому их мы просто оставляем как есть, в шапочках. Корень из четырех равен двум. Теперь всё это добро нужно разделить по-братски - пополам. Делим каждое полученное число на 2. Ноль, деленный на два, равняется нулю. Остальное вы знаете - что не делится, то записываем так, как есть - в виде дроби. В результате этого экзамена по каллиграфии мы получили значения тригонометрической функции синус с дробями и корнями для углов 0, 30, 45, 60 и 90 градусов. Вот видеоролик.



Вот как это выглядит на картинке. Для получения значений косинуса снова решать ничего не нужно. Достаточно перестроить наш пионерский отряд от конца к началу или записать значения углов от 90 градусов до нуля.

Как запомнить значения тригонометрических функций

В англоязычной Википедии этот же процесс подан как половина квадратного корня из тех же чисел 0, 1, 2, 3 и 4. Мы получили значения синуса нуля, тридцати, сорока пяти, шестидесяти и девяноста градусов.

Как запомнить значения тригонометрических функций

Как быть, если вам нужен тангенс одного из этих углов? Очень просто. Решаем ещё один детский пример, в котором значение синуса делим на значение косинуса такого же угла. Или значение косинуса на синус - для котангенса. Напоминаю, что для того, чтобы разделить одну дробь на другую, нужно первую дробь умножить на перевернутую вторую (обратную, в которой числитель и знаменатель меняются местами).

В результате подстановки полученных значений в нужный пример у вас что-то с чем-то должно сократиться. Обычно для этого применяются значения тригонометрических функций с корнями и дробями.

Вот ещё один способ, как запомнить значения тригонометрических функций - математика на пальцах. Эта шпаргалка будет всегда при вас и ни один учитель не сможет её отобрать.

Как запомнить значения тригонометрических функций

Единственный недостаток этого способа - арифметика. С детства нас учили на руке считать пять пальцев, а тут вдруг - четыре! Весь фокус в том, что с детства мы пальцы считаем, начиная с единицы. В случае со значениями тригонометрических функций, пальцы нужно начинать считать с нуля. Вот так один палец и исчезает.

В заключение совсем не лишним будет рассказать вам, как запомнить тригонометрические функции. До этого изобретения я всегда смотрел в справочник по математике, где находится косинус, а где - синус. После изобретения своей полезной картинки, я вообще перестал в справочник заглядывать при решении задач. Мне проще самому вывести все формулы, чем разобраться в том, что там математики в справочнике насочиняли.

Успехов вам на экзаменах!!!

Как найти решение системы уравнений

Подкинули мне тут не простую систему уравнений для решения. Как найти решение системы уравнений, если в одном уравнении неизвестные в первой степени, а в другом - во второй? Посмотрите сами.

Как найти решение системы уравнений

Вот такая вот фигня, девочки, досталась нам в наследство от наших предков - составителей учебников. Здесь определенно нужно шевелить мозгами, чтобы во всем разобраться.

С первым уравнением мы поступим очень мудро: оно нас не трогает и мы его пока трогать не будем. Мы в любой момент, при помощи этого уравнения, можем выразить икс через игрек или игрек через икс. Как мы того пожелаем.

Со вторым уравнением нам придется повозиться. Давайте посмотрим на это уравнение не конкретно, а в общем, одним глазом. Все те штучки, которые в нем имеются, очень напоминают останки динозавров, которые назывались "формулы сокращенного умножения". Жили эти динозавры в младших классах и вымерли в нашей памяти сразу же по окончании учебного года. Вот теперь нам предстоит поковыряться в этой кучке математического мусора и определить, какому из динозавров что принадлежит. Для этого нужно взять каталог этих доисторических чудовищ, в котором описан внешний вид каждого из них. Хм, а у меня здесь такого нету. Безобразие! Придется по памяти.

И так, приступаем. Квадрат одной штучки, квадрат другой штучки, удвоенное произведение этих штучек... Вау! Да это же квадрат суммы или разности! Но разбросаны они по уравнению как попало. Берем веник и сметаем их в левую часть уравнения, попутно раскладывая по полочкам. При этом не забываем главное правило математического пинг-понга: при пересечении знака равенства вся математическая фигня меняет свой знак на противоположный - минус на плюс, плюс на минус. Такой себе обязательный обменный пункт на математической таможне. Когда всё собрано согласно древней инструкции, прекрасно видно, что эти останки принадлежали динозавру по имени "Квадрат разности". Преобразовываем ископаемые останки в первозданный вид.

Нам немножко полегчало, но первозданной красоты всё равно не наблюдается. Что здесь делает девятка, в правой части уравнения? Как она сюда попала? Допустим, это перебежчик через знак равенства из левой части. Присмотримся к нему по-внимательнее... Да это же вражеский шпион по кличке "Три в квадрате"! Учиняем маленький дипломатический скандал и выдворяем его на родину - в математике нет тюрьмы, куда его можно было бы посадить. Шпион, не шпион, а на математический таможне правила для всех одинаковы: пересекаешь знак равенства - будь добр поменять знак. И что же у нас получилось в результате? В правой части уравнения ничего не осталось. Страшно остаться без ничего? В жизни - да, в математике - нет. Пишем ноль и никаких проблем. А что с левой частью? В левой части нарисовался динозавр по имени "Разность квадратов". Как живой. Нужно его срочно умертвить - разложить по формуле. В результате мы получем одну скобочку умноженную на вторую скобочку и всё это равняется нулю.

Как найти решение системы уравнений

Что нам говорит последнее уравнение? Нулю оно может равняться только в том случае, если одно из выражений в скобках будет равно нулю. Не важно, какое. Мы можем любое выражение в скобке приравнять к нулю и никаких неизвестных во второй степени у нас не будет. Так, пора прекращать наши палеонтологические раскопки и дипломатическую грызню. Смотрим, какая система уравнений у нас получилась.

Как найти решение системы уравнений

Вы можете сказать, что так не честно - в формуле разности квадратов одна буковка возводится в квадрат возводится не буковка. Так вот, математике безразлично, что вы спрячете под буковкой - одну буковку или целый роман "Война и мир" - формула всегда работает одинаково. Смотрите, как это делается. Тупо берете и тупо преобразуете: "разность квадратов войны и мира равна произведению суммы войны и мира на разность войны и мира".

Как найти решение системы уравнений

Но вернемся к нашей системе двух динозавров с двумя неизвестными. Пот теперь пришло время потревожить наше первое уравнение. Выразим икс через игрек и подставим его во второе уравнение. В итоге этих манипуляций ми получим одно уравнение с одним неизвестным.

Как найти решение системы уравнений

Теперь приравняем к нулю каждую из скобок и решаем два уравнения. В результате этого решения ми получим два значения игрека.

Как найти решение системы уравнений

Подставив каждое из найденных значений игрека в первое уравнение, мы получим два значения икс.

Как найти решение системы уравнений

Вот теперь всё - наша система уравнений решена, мы нашли две пары значений неизвестных икс и игрек. Вам остается только оформить это решение согласно действующих в данный момент бюрократических правил оформления домашних заданий. Когда сегодняшние бюрократы вымрут, на их смену придут новые бюрократы с новыми правилами оформления. Станете мамами, бабушками - вспомните мои слова. Бюрократы - не динозавры, они живут вечно.

Ну и последнее. Сделайте проверку, подставив найденные значения неизвестных в исходные уравнения. Вы увидите, что весь этот сыр-бор был затеян ради подтверждения правила - от перестановки слагаемых сумма не меняется.

Решение системы уравнений методом сложения

Сегодня, по просьбе учащихся, мы рассмотрим решение системы уравнений методом сложения. Дана нам система двух линейных уравнений с двумя неизвестными. Обычно я такие системы уравнений решаю методом подстановки, но в данном случае даже мне понятно, что лучше использовать другой метод - метод сложения уравнений.

Как складывать уравнения? Так, как нас учили в детском садике - собачки с собачками, зайчики с зайчиками. Применительно к линейным уравнениям с двумя неизвестными мы складываем иксы с иксами, игреки с игреками, числа с числами. В уравнениях неизвестные выполняют ту же роль, которую выполняют единицы измерения в нашей повседневной жизни - определяют возможность или невозможность выполнения математической операции сложения. При сложении двух уравнений с двумя неизвестными одно неизвестное должно исчезнуть. Вместо двух уравнений с двумя неизвестными у нас получается одно уравнение с одним неизвестным.

В каждом из уравнений у нас имеется три типа слагаемых - иксы, игреки, числа. Для сложения двух уравнений нам нужно выполнить три операции сложения, по одной для каждого слагаемого. Подобным образом можно складывать миллион уравнений с миллионом неизвестных. Главное не потерять смысл сложения уравнений: что вы будете делать с одним уравнением, в котором миллион неизвестных? Возвращаясь к нашей сладкой парочке, запишем в отдельных строках сложение разных членов уравнения.

Решение системы уравнений методом сложения. Шаг 1.

И так, игрек у нас исчезает. Из неизвестных остается только какое-то количество иксов и число к ним в придачу. Это и будет одно уравнение с одним неизвестным. Решать такие уравнения нас уже учили.

При решении полученного уравнения мы узнаем, что наш икс равняется минус единице. Это научное открытие используем для нахождения значения игрека. В одно из уравнений нашей системы подставляем найденное нами значение икс и мы снова наступаем на те же грабли - получаем одно уравнение с одним неизвестным. Только на этот раз наше неизвестное обозначено буквой игрек. Лично мне больше нравится первое уравнение. Вот в него я и вставлю вместо икса полученное значение.

Решение системы уравнений методом сложения. Шаг 2.

Как видите, в математике очень трудно найти что-то новое. Всё новое - это хорошо замаскированное старое. Ещё раз решаем уравнение и получаем значение игрек. Всё очень просто: два неизвестных - два решения уравнений; миллион неизвестных - миллион решений (по одному решению на каждое неизвестное). Про миллион я, конечно, шучу. Нет такого математика, который сможет придумать такую систему уравнений с миллионом неизвестных, которая решается так просто.

У меня нет преподавателя математики, который мне скажет, правильно я решил систему уравнений или нет. Поэтому я воспользуюсь математикой и сам проверю свое решение. Для этого в оба уравнения вместо неизвестных я вставлю их значения, полученные мною в ходе решения.

Решение системы уравнений методом сложения. Шаг 3.

Равенство в обеих выражениях сохраняется, значит система уравнений решена правильно. Советую и вам всегда выполнять проверку. Даже если в ответах на последней странице учебника или в решебнике будет опечатка, проверка тут же её обнаружит.