Преобразование тригонометрических функций - правило прямого угла.

Преобразование тригонометрических функций - правило прямого угла не ищите в учебниках. Такого математического правила нет ни в одном учебнике математики. Это придумал я в результате нудного ковыряния в формулах приведения тригонометрических функций. Оказывается, если отбросить знаки тригонометрических функций, всё становится простым и понятным. На уроках математики всего того, что вы прочтете ниже, я не советую рассказывать - преподаватели математики могут обидеться, что вы знаете больше них. А вот для проверки правильности своих решений правило прямого угла вам очень даже пригодится.

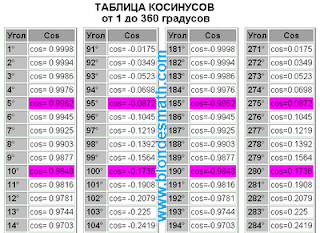
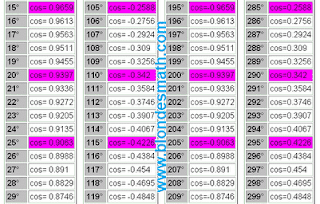
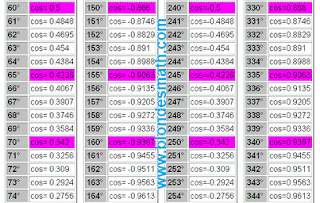
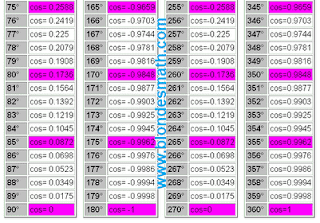
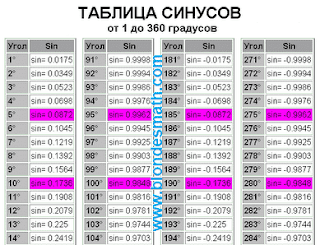
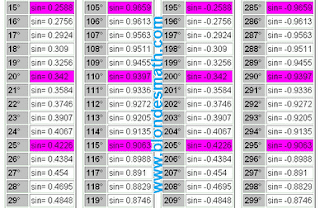
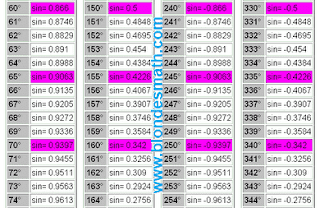
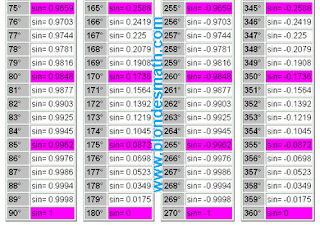
Первым делом разделим все тригонометрические функции на три пары перпендикулярно симметричных функций: синус и косинус, тангенс и котангенс, секанс и косеканс. Понятие перпендикулярной симметрии тригонометрических функций в математике отсутствует, хотя именно на её свойствах основано действие правила прямого угла и формул приведения тригонометрических функций. О перпендикулярной симметрии мы поговорим в другой раз. А пока принимайте на веру мои слова, ведь вся математика построена исключительно на вере в правильность принятых определений)))

Вот теперь можно сформулировать правило прямого угла:

если к величине угла альфа любой тригонометрической функции прибавить прямой угол, название тригонометрической функции изменится на перпендикулярно симметричное при условии сохранения угла альфа в качестве аргумента тригонометрический функции. Изменение знаков полученных тригонометрических функций необходимо рассматривать дополнительно.

Получилось очень заумно и не понятно (на всякий случай писал специально для математиков). Не надо пугаться, учить дословно этот бред не нужно, главное - понять принцип действия. Давайте посмотрим, как это правило выглядит на картинке.

Правило прямого угла

На рисунке вы видите три совершенно одинаковых крестика со стрелочками. Стрелочки указывают на названия тригонометрических функций. Сгруппированы тригонометрические функции по признаку перпендикулярной симметрии.

Как это работает? Выбираете нужную вам тригонометрическую функцию и движетесь по часовой или против часовой стрелки вокруг центра крестика на нужное вам количество прямых углов. В конце движения стрелочка показывает, какое название тригонометрической функции получится в результате. При каждом добавлении или вычитании прямого угла название тригонометрической функции меняется. Формулы приведения дают нам конечный результат, правило прямого угла позволяет проследить процесс получения этого результата. Например:

Правило прямого угла пример sin

Правило прямого угла пример tg

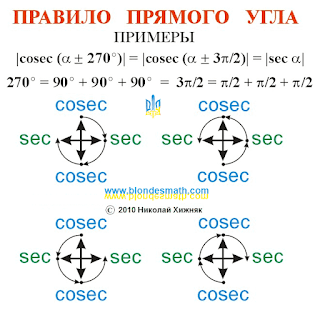Правило прямого угла пример sec

Вертикальные черточки означают модуль тригонометрический функции, то есть без учета изменений знаков. Данный принцип действует как для сложения, так и для вычитания прямых углов. Каждый раз, прибавляя или отнимая прямой угол, нужно менять название функции.

Как видно из приведенных выше рисунков, результат преобразования не зависит от того, в каком месте вы возьмете тригонометрическую функцию (слева или справа, сверху или снизу) и в каком направлении вы будете отсчитывать прямые углы (по часовой стрелке или против часовой стрелки). Вот это и есть настоящая математика - результат не зависит от порядка выполняемых нами действий.

Общий принцип следующий: если количество прибавляемых или вычитаемых прямых углов нечетно - название тригонометрической функции меняется, если количество прямых углов четно (то есть делится на два) - название функции не меняется.

Принцип изменения названия тригонометрических функций очень похож на правило умножения положительных и отрицательных чисел. Помните? Минус на минус дает плюс, плюс на минус дает минус. Только у нас один прямой угол меняет название функции, два прямых угла не меняют название. Как этим пользоваться на практике, рассмотрим на примерах в следующий раз.

Как определять знаки полученных тригонометрических функций? Включайте свою сообразительность, берите тригонометрический круг - и вперед. Я подумаю, можно ли здесь ввести какой-то общий принцип, но результата не гарантирую. Секрет знаков тригонометрических функций заключается в том, что настоящие тригонометрические функции знаков не имеют - их придумали математики. Мы с вами тоже можем ввести в математику цвет, вкус, запах, политическую или религиозную принадлежность тригонометрических функций. Что скажет по этому поводу математика? Вы сами это придумали, сами с этим и разбирайтесь - чем бы дитя не тешилось, лишь бы не плакало.

Если у вас есть вопросы по применению правила прямого угла, пишите в комментариях.

Вы ищете:

Не понимаю формулы приведения - прочтите эту страничку, возможно что-то прояснится.

Больше о новых взглядах на математику и её проблемах смотрите на странице "Новая математика"

Котангенс формулы приведения

Котангенс формулы приведения - последняя картинка из серии картинок формул приведения тригонометрических функций.

Котангенс формулы приведения

Я не буду сильно много писать о формулах приведения котангенса, для формул синуса, косинуса и тангенса написано достаточно, не буду повторяться. Скажу пару слов о другом.

Наверное, как всякая блондинка, я очень туго соображаю. В процессе подготовки к публикации формул приведения котангенса, до меня наконец-то дошло, что всю эту гору формул можно заменить одним простым правилом, касающимся названий тригонометрических функций и изобразить это правило в виде очень простой и наглядной картинки - ведь в настоящей математике всё должно быть очень просто и наглядно. Сейчас нарисую. В следующей публикации встречайте новое математическое правило прямого угла для преобразования тригонометрических функций. Надеюсь, это правило поможет вам лучше понимать формулы приведения котангенса.

Тангенс формулы приведения

Тангенс формулы приведения - продолжаем расписывать таблицу формул приведения для тригонометрической функции тангенс tg. Традиционно, в первой строчке написана формула тангенса для отрицательного угла. Поскольку тангенс считается нечетной тригонометрической функцией, то при изменении знака угла изменяется знак значения тригонометрической функции тангенс. На языке математиков эта фраза звучит, конечно, совсем иначе. Можете открыть учебник и почитать. Как и синус, тангенс является заразной функцией и передает вирус под названием "знак минус" от угла к значению тангенса.

Тангенс формулы приведения

Над надписью "Математика для блондинок" расположены два блока по четыре формулы, наглядно подтверждающие когда-то выученное нами правило - от перестановки слагаемых результат не изменяется. Это правило работает и в тригонометрических функциях. В частности, для тангенса, а ещё точнее - для суммы углов. Это правило выполняется во всех тригонометрических функциях.

Ещё одна интересная особенность тригонометрической функции тангенс - если к углу альфа прибавить другой угол или отнять другой угол, то значения тангенса полученных угла не будут отличаться. Два последних блока по 4 формулы являются наглядным доказательством. Если я не прав - поправьте меня в комментариях. Наверное, тангенс является морально устойчивой тригонометрической функцией и не реагирует на разного рода приставания к его углам - с хорошими (знак плюс, сумма) или с плохими (знак минус, разность) намерениями.

В завершение нашей небольшой экскурсии по формулам приведения тангенса, нужно ответить на самый главный вопрос - что делать с результатом? А результат, тангенс или котангенс угла альфа, можно обменять на числа (как доллар на рубли) в обменном пункте тригонометрических функций - это таблицы тангенсов и котангенсов. Точно также, как и доллар, полученный результат в виде тангенса или котангенса угла альфа можно не менять на числа, а сохранить на будущее - а вдруг он сократится в тригонометрическом выражении.

Прямоугольный угол

Прямоугольный угол - это весьма оригинальное сочетание слов "прямоугольный" и "угол". Появилось оно, скорее всего, в результате весьма эффективного метода работы - это метод кройки и шитья. Как получить фразу "прямоугольный угол" в домашних условиях? Очень просто. Берем любую устойчивую фразу со словом "прямоугольный", например, "прямоугольный треугольник" или "прямоугольная трапеция" и ножничками отрезаем от этой фразы второе слово. Выбрасываем отрезанное слово в мусор за ненадобностью. Затем берем фразу "прямой угол" и отрезаем от неё первое слово и так же выбрасываем в мусор. К первому слову первой фразы ниточками пришиваем второе слово второй фразы. Можно прилепить скотчем или приклеить клеем. У нас получилась фраза "прямоугольный угол". Кстати, мы таким способом на работе часто чертежи делаем: из одного чертежа вырезаем нужный фрагмент, наклеиваем на другой чертеж в нужное место, прогоняем через ксерокс - новый чертеж готов. Прямо как прямоугольный угол.

Если же вы решили в Интернете найти прямоугольный угол, вынужден вас разочаровать - даже здесь такие звери не водятся. Вам нужно сперва определиться, что же именно вы имеете в виду под прямоугольным углом. Как я уже говорил, за этим могут скрываться прямой угол, прямоугольный треугольник, прямоугольная трапеция и ещё целое море разных прямоугольных штучек.

Если же вы желаете увидеть, как выглядит прямой угол и случайно набрали фразу прямоугольный угол, то посмотреть на него можно прямо здесь и сейчас на картинке ниже.

Прямой угол

Учителям математики нужно объявить выговор за то, что сотни людей в день рыщут по интернету в поисках прямоугольного угла. В математике, даже в устах блондинки, это будет звучать примерно, как "косметическая косметика" или "автомобильный автомобиль". Советую фразу прямоугольный угол в слух не произносить, а посмотреть в учебнике или в шпаргалке, как правильно называется то, что вы ищете.

Синус формулы приведения

Синус формулы приведения - это продолжение расшифровки китайской грамоты таблицы формул приведения тригонометрических функций. По аналогии с формулами приведения косинуса, в самом верху написана формула преобразования синуса отрицательных углов. Если возле угла альфа будет стоять знак минус, значит нужно взять тригонометрическую таблицу синусов, найти там значение синуса для угла альфа без знака минус, прежде чем записать это значение в тетрадку, нужно поставить знак минус, и только после этого знака минус можно писать циферки из таблички. Вся эта не простая процедура означает, что мы имеем дело с нечетной тригонометрической функцией. У нечетных тригонометрических функций знак минус от угла передается значению тригонометрической функции, как заразная инфекция, против которой даже вакцинация бессильна.

Синус формулы приведения

Как вы видите на картинке, формулы начинаются с перевода углов из радиан в градусы. Для углов в градусах и радианах формулы будут выглядеть абсолютно одинаково, за исключением того, что вместо циферок с пи будут другие циферки с градусами. В формулах приведения даны суммы и разности углов в разных комбинациях. В зависимости от выражения в скобках, все формулы приведения синуса sin в результате дают положительные или отрицательные значения синуса или косинуса угла альфа. При этом угол альфа не обязательно должен быть в пределах от нуля до 90 градусов (или пи/2). Значение угла альфа может быть любым. Формулы приведения можно применять многократно к полученным результатам. Тот же угол альфа из диапазона 0 - 90 градусов по формулам приведения можно преобразовать в угол большей величины.

Полученные по формулам приведения значения тригонометрических функций угла альфа можно взять из таблицы синусов (ссылка выше) или таблицы косинусов.

Косинус формулы приведения

Формулы приведения косинуса расписаны довольно подробно для самых разных углов. Начнем с того, что тригонометрическая функция косинус является четной тригонометрической функцией. А это как? На знак минус перед значением угла при нахождении косинуса можно вообще не обращать внимания. Как будто минуса нет совсем. Значение косинуса отрицательного угла альфа будет точно таким же, как и значение косинуса положительного угла альфа. Как видите, есть в математике такие штучки, которые имеют иммунитет к отрицательным значениям. На картинке вы можете увидеть эту формулу в самой верхней строчке.

Косинус формулы приведения

Первый столбик в формулах образуют углы в радианной и градусной мерах. В радинах измеряются те углы, которые имеют волшебную буковку пи. Пи/2, пи, 3пи/2 и 2пи - это и есть значения угла в радианах. Им соответствуют 90, 180, 270 и 360 градусов. Это записано для тех, кто испытывает затруднения в переводе углов из градусов в радианы и обратно. Такой себе пешеходный тригонометрический переход. Улица называется "Угол", а у этой улицы есть два тротуарчика для пешеходов. Один тротуарчик называется "Радианы", с его стороны дома имеют номера пи/2 (пи пополам), пи, 3пи/2 (три вторых пи), 2пи (два пи) и так дальше до самой Америки))) Другой тротуарчик называется "Градусы", здесь дома имеют номера 90, 180, 270, 360 и так дальше. Когда мы стоим на этой улице, свое точное местоположение мы можем определять по номеру ближайшего дома. Этот номер будет или в радианах, или в градусах, смотря на каком тротуаре мы стоим и в какую сторону от дороги смотрим. Допустим, ми прочли адрес "Угол 3пи/2". Переходим на противоположную сторону улицы - мы уже находимся по адресу "Угол 270 градусов". Место одно и то же, но называется по-разному. Таковы причуды придуманной нами математики. Но мы немного отвлеклись от формул приведения косинуса.

Над надписью "Математика для блондинок", в среднем столбике, расположены формулы приведения косинуса для суммы углов. Если большой угол представить в виде суммы разных комбинаций прямого угла (угол в пи/2 или 90 градусов называется прямым) и угла альфа, то кусочки такого угла, кратные прямому углу, можно выбросить. Вместо косинуса большого угла, мы получим значение косинуса или синуса острого угла (углы от 0 до пи/2 радиан или от 0 до 90 градусов называются острыми). Теперь это значение можно довольно просто найти по таблице косинусов или таблице синусов. Кстати, в этих таблицах даны значения для углов аж до 360 градусов или 2пи. Можете проверить формулы приведения, сравнив значения для больших углов и острых углов, выполнив преобразования по формулам приведения.

Ниже на картинке написаны формулы приведения для разности комбинаций прямых углов и угла альфа. То есть, если большое значение угла представить как комбинацию прямого угла минус угол альфа.

В последнем столбике представлены формулы приведения для случая, если мы к углу альфа будем прибавлять или вычитать из угла альфа комбинации из прямых углов. Например, если к углу альфа прибавить прямой угол, то косинус этакого угла будет равен отрицательному значению синуса исходного угла альфа. Если из угла альфа вычесть прямой угол, то косинус такого угла будет равняться синусу исходного угла альфа.

Формулы приведения таблица

Формулы приведения тригонометрических функций - это ... это ... в учебнике почитайте, там правильно написано. Ничего общего с привидением Каспером эти формулы не имеют. Слово "привидение" происходит от слова "видеть", слово "приведение" происходит от слова "вести". Короче, при помощи этих формул можно загнать всех тригонометрических баранов в одно стойло с углом от нуля до 90 градусов. Формулы приведения в таблице выглядят так:

Формулы приведения таблица

Действительно, это похоже на тригонометрический Хэллоуин, когда одни тригонометрические функции наряжаются в другие тригонометрические функции и пугают нас своими большими углами. Не надо пугаться, по сути, все они безобидные, как доброе привидение Каспер. Давайте в следующий раз разберем по косточкам всю эту китайскую грамоту, зашифрованную в таблице и распишем формулы приведения тригонометрических функций в обычном виде.

Расшифровку формул приведения косинуса, синуса можно посмотреть на отдельных страницах. То, что здесь собрано в таблицу для компактности, там расписано самым подробным образом. И там формул приведения больше, чем представлено здесь в таблице. Что такое угол в радианах и градусах? Что такое четная и нечетная тригонометрическая функция? На этих страницах есть образные сравнения этих понятий с простыми вещами.

Математика блондинок и не только...

Сегодня для блондинок проведем урок биологической математики. Удивительно, но факт:

если подсчитать количество волос на голове человека (а это чистая математика без всяких предрассудков), то результаты вычисления окажутся такими: у блондинок их около 150000 (сто пятьдесят тысяч), каштановых волос на голове мы насчитаем около 110000 (ста десяти тысяч), черных волос окажется около 100000 (ста тысяч), рыжих - 90000 (девяносто тысяч). Блондинки! Вы обладаете самой густой шевелюркой среди всех человеков! Причем, это не досужая выдумка лысого автора блога "Математика для блондинок", а подтвержденный математикой факт;

Блондинка и математика

число верхних ресниц составляет от 150 до 200, нижних - от 50 до 100 (ужас, но даже у блондинок число нижних ресниц в 2 - 3 раза меньше , чем число верхних ресниц - здесь даже Максфактор бессилен (прямо как у Арестовича 2 - 3 недели, примечание 2023 года, чтоб вы не подумали, что я тогда уже всё знал);

длинна ресниц, измеренная самой заурядной линейкой для измерения длинны ресниц, для верхних ресниц дает результат 8 - 12 миллиметров, для нижних равняется 6 - 8 миллиметров (вот здесь уже есть где разгуляться не только Максфактору, но и накладным ресницам);

величина дневного роста волос на голове составляет 0,5 - 0,7 миллиметра (специально для блондинок напишу буковками эти страшные числа - пять десятых и семь десятых миллиметра) - это меньше самого крохотного деления на вашей школьной линейке почти в два раза, а вот дневной рост волос бороды аж на одну десятую миллиметра больше - от 0,6 до 0,8 за день (блондинкам это не угрожает, так же, как мне - рост волос на голове).

И ещё несколько печальных фактов из жизни волосатых. Дневное выпадение волос на голове - от 50 до 120 штук (интересно, почему же я лысый???!!! Куда смотрит математика?!). Продолжительность жизни волос составляет от 2 до 4 лет. Продолжительность жизни ресниц составляет всего 150 (сто пятьдесят!) дней. Вы представляете?! Уже через полгода на ваших глазах не будет ни одной знакомой ресницы - все новые! Ужас!!!

Фотография самым бесстыдным образом стырена с женского интернет-журнала Ledi Правда. Где её стырили они - я не знаю)))

Синус и косинус 11 градусов и 32,7 минут как вычислить?

Когда я учился в школе, мне приходилось пользоваться таблицей Брадиса для нахождения синусов, косинусов, тангенсов и котангенсов. Уже забыл, как этой таблицей пользоваться. Но сегодня мы живем в компьютерном веке, а что такое компьютер? Правильно, это такой большой калькулятор. А в каждом большом калькуляторе должен быть калькулятор маленький. Вот этим калькулятором и нужно воспользоваться. У меня операционная система Windows XP, на экране слева, внизу, есть кнопочка "Пуск". Нажимаете эту кнопочку, затем в меню выбираете "Все программы", из всех программ выбираете "Стандартные". В стандартных программах прячется нужный нам калькулятор синусов и косинусов.

Калькулятор синусов и косинусов

Сам калькулятор обычно не имеет синусов и косинусов. Нужно нажать кнопочку "Вид" в верхней панельке калькулятора и выбрать "Инженерный". В инженерном калькуляторе есть нужные нам кнопочки синус "sin", косинус "cos" и тангенс "tg".

Калькулятор синусов и косинусов

После этого нужно проследить, что бы в калькуляторе была включена десятичная система счисления и градусы для углов. Для этого нужно нажать пыптик "Dec" и пыптик "Градусы", как на картинке показано. Наш инструмент для нахождения синусов и косинусов готов. Теперь приступим непосредственно к процессу добычи полезных тригонометрических ископаемых.

Если вам не удалось выковырять калькулятор из своего компьютера, не отчаивайтесь! Специально для вас я разместил в этом блоге "Математика для блондинок" калькулятор бесплатно, которым вы можете воспользоваться прямо здесь и сейчас!

Сперва минуты нужно перевести в градусы. Для этого 32,7 делим на 60. В результате получаем 0,545 градуса. На 60 делим потому, что в одном градусе 60 минут. К полученной циферке прибавляем 11 градусов, которые у нас уже есть, и получаем 11,545 градусов. Вот из такого угла на калькуляторе можно уже извлекать синусы и косинусы. Для этого нужно просто нажать кнопочку "sin" или "cos".

Весь процесс нажимания кнопочек выглядит так:

32,7 / 60 + 11 = sin

В результате в окошке калькулятора появится число 0,20013750391127021629780041181162

Математически это записывается так:

sin (11° 32,7') = sin 11,545° = 0,2001

Для косинуса угла 11 градусов 32,7 минут значение равно почти единице и запишется так:

cos (11° 32,7') = cos 11,545° = 0,9798

Для тангенса выполняется всё точно также, только в самом конце вместо кнопочки "sin" нажимается кнопочка "tg". Вот с котангенсами, кажется, проблема. Нет такой кнопочки в калькуляторе! Но мы умные, и помним, что тригонометрическая функция котангенс является обратной тригонометрической функцией по отношению к тангенсу (столько умных слов за один раз - аж самому страшно!). На практике это выглядит очень просто: сперва находим тангенс, как описано выше. Когда циферки тангенса появились в окошке калькулятора, нажимаем на кнопочку "1/х". Циферки тангенса поменяются на циферки котангенса. А эта дополнительная волшебная кнопочка называется "число, обратное введенному". Ради прикола, введите число 2, нажмите эту волшебную кнопочку и у вас появится число 0,5 что равно 1/2.

Для перевода секунд в минуты, секунды так же нужно разделить на 60, поскольку в каждой минуте 60 секунд. Для перевода в градусы, полученные минуты нужно ещё раз разделить на 60:

1" = 0.016667' = 0,00027778°

Вот, кажется, всё о том, как вычислить синус и косинус 11 градусов и 32,7 минут. Если у кого-то остались вопросы, пишите в комменты.

Для своих любимых блондинок могу дать несколько маленьких подсказок. Синус 6 градусов 30 минут нужно на калькуляторе набирать как 6,5 градусов, потом нажать кнопочку синуса.

Теперь примерчик посложнее, с секундами: косинус 6 градусов 7 минут 9 секунд. 9 секунд делим на 60, прибавляем 7 минут, снова делим на 60, прибавляем 6 градусов. Должно получиться число 6,11916666... градусов. Теперь нажимаем кнопочку косинуса "cos". Порядок нажимания кнопочек такой:

9 / 60 + 7 / 60 + 6 = cos

Математически пересчет градусов, минут и секунд в градусы для 6 градусов 7 минут 9 секунд можно записать так:

(9 : 60 + 7) : 60 + 6 = 6,11916666...

В общем виде для угла в x градусов, y минут, z секунд формула перевода в градусы будет выглядеть так:

(z : 60 + y) : 60 + x = градусы

Надеюсь, эта формула вам пригодится.

У меня 720 градусов, как дальше найти синус и косинус альфа?

"А что если при нахождении значения альфа равному 4пи, у меня 720 градусов, как дальше найти синус и косинус альфа??" - такой вопрос был задан в комментариях. Действительно, как найти тригонометрическую функцию, если угол альфа больше 360 градусов?

Представьте, что все углы больше 360 градусов или 2 пи - это клубок пряжи. Для того, чтобы узнать значения тригонометрических функций для таких углов, этот клубок пряжи нужно сначала размотать. Один виток пряжи равняется углу в 360 градусов или 2 пи. Разматывать клубок нужно до тех пор, пока значение угла не станет меньше 360 градусов или 2 пи. После этого по таблице значений тригонометрических функций или по тригонометрическому кругу находим значение нужной тригонометрической функции.

720° - 2 x 360° = 0°

Этот же фокус с углами в радианах будет выглядеть так:

4π - 2 x 2π = 0

Для угла 720 градусов или 4 пи получается, что синус и косинус такие же, как и для угла 0 градусов. Решение можно записать так:

sin 720° = sin 4π = sin 0 = 0

cos 720° = cos 4π = cos 0 = 1

Синус 720 градусов или 4 пи равен синусу нуля градусов и равен нулю. Косинус 720 градусов или 4 пи равен косинусу нуля градусов и равен единице.

Математика - блондинка ищет икс

Блондинка ищет икс - это классическая картинка, над которой смеялся весь Интернет. Посмеялись и мы. А теперь попробуем разобраться, так ли уж смешно. Что сказано в задании? "Найдите х". Что сделала блондинка? Она нашла икс и показала его. Где сказано, что искать нужно ЗНАЧЕНИЕ икс? Помните свое детство, когда мама вам говорила "Покажи на картинке зайчика". Вы тыкали пальчиком в зайчика на картинке, а ваша мама восхищалась своим самым умным ребенком.

Задание "Найдите х" можно понимать по разному. Блондинка, с инженерной точки зрения, выполнила задание блестяще - с наименьшими затратами времени и сил. Давайте на минутку заглянем в любой офис. Директор говорит менеджеру по закупкам (сейчас модно всех обзывать менеджерами): "Найди ..." - и называет товар. Что, менеджер выгребает из бухгалтерии все деньги и закупает на всю сумму названный товар? Нет. Хоть он и является менеджером по закупкам, он просто собирает всю информацию по названному товару. Эту информацию он передает директору. И уже директор решает, где, сколько и по какой цене товар нужно купить. Или покуда вообще не покупать. Так поступают все нормальные менеджеры.

Действительно, окружающая обстановка налагает некоторый стереотип поведения. Как у дрессированных животных. Если вы менеджер по закупкам, без прямого указания что именно покупать, покупать ничего не надо. Что бы вам не говорили. Если вы в школе проходите решение уравнений, значит по команде "найдите х" вы должны искать значение "икс", а не крестик на картинке. Так поступают все умные (так и хочется написать "обезьянки") ученики.

А блондинки - они другие. Они хорошо помнят, чему их учили в детстве. Детское решение они считают более простым. Действительно, зачем париться с каким-то решением, когда можно просто показать на картинке этот самый то ли икс, то ли крестик. Вы считаете себя уже взрослым, и смеетесь над наивным детским решением блондинки? А давайте посмотрим на вас, взрослого, значения иксов находящего, на другом уроке...

... И так, вы на уроке географии, стоите с указкой в руках возле карты и учительница говорит вам: "Найдите Гондурас". Вы лихорадочно шарите глазами по карте в поисках Гондураса, но его нигде нет! Здесь вам уже ничто не может помочь - ни умение находить значение икса, ни знание теоремы Пифагора... Всё, что от вас требуется - это тупо ткнуть указкой в этот злополучный Гондурас. Вы растерянно смотрите в класс, где десятки пальцев показывают в самые разные уголки земного шара и вы еще больше теряетесь. Невидящим взглядом уставившись в карту, вы вдруг понимаете, что учительница специально для вас принесла сегодня на этот урок карту БЕЗ ГОНДУРАСА!!! Обреченно опустив указку и глаза, в самом низу карты, вы отчетливо видите надпись крошечными буквами - её даже в лупу прочитать невозможно! Но вы уже точно знаете, что там написано "Отпечатано в типографии "Месть учителя". Тираж 1 экземпляр (без Гондураса)"...

Сколько будет метров и дециметров?

"Сколько будет 22 метра 2 дециметра минус 1 метр 8 дециметра?" Трудность этой задачи заключается в том, что для обозначения одного числа используется сразу две единицы измерения: метры и дециметры. Если перевести сказанное на нормальный язык блондинок, то это почти то же самое, что фразу "Я вчера купила две кофточки и одну подарила подружке" заменить фразой "Я вчера купила две кофточки и четыре рукава, а потом одну кофточку и два рукава подарила подружке". Естественно, что последняя фраза вас сразу собьет с толку: "А рукава что, отдельно от кофточек продаются?". Конечно же, нет. Рукава пришиты к кофточкам, вот только считаем мы их отдельно. Зачем? Что бы вас запутать. Задачки в математике всегда запутываются, как клубок ниток. Вы должны их распутать и получить правильный ответ. Это развивает сообразительность, вот. А простое списывание с решебника развивает тупость. Теперь приступим к решению.

Значит, задачка у нас такая: сколько будет, если от 22 метров и 2 дециметров отнять 1 метр и 8 дециметров? Главное, что нужно знать при решении этой задачки - сколько дециметров в одном метре? Или сколько метров в одном дециметре.

1 метр = 10 дециметров

1 дециметр = 0,1 метров

Один метр равен десяти дециметрам. Один дециметр равен одной десятой метра. Вот теперь у нас есть всё, что бы решить задачку. Есть целых три способа решения этой задачи - в метрах, в дециметрах, в двух единицах измерения сразу.

Решаем задачку в метрах. Для этого дециметры уменьшаемого (это то число, из которого вычитают) и вычитаемого (это то число, которое вычитают) переводим в метры.

2 дециметра = 0,2 метра

8 дециметров = 0,8 метра

Прибавляем эти хвостики к нашим числам в метрах:

22 метра + 0,2 метра = 22,2 метра

1 метр + 0,8 метра = 1,8 метра

Теперь можно выполнить вычитание и получить разность этих самых метров. Ответ можно сразу перевести в метры и дециметры:

22,2 метра - 1,8 метра = 20,4 метра = 20 метров 4 дециметра

Второй способ - это решить эту же задачку в дециметрах. Для этого переведем метры в дециметры:

22 метра = 220 дециметров

1 метр = 10 дециметров

К полученным дециметрам прибавляем те дециметры, которые у нас есть по условию задачи:

220 дециметров + 2 дециметра = 222 дециметра

10 дециметров + 8 дециметров = 18 дециметров

Выполняем вычитание и переводим дециметры снова в метры и дециметры:

222 дециметра - 18 дециметров = 204 дециметра = 20 метров 4 дециметра

Это была математика. Теперь для блондинок. Что бы разобраться, что же мы делали, давайте заменим метры на бантики, а дециметры на рюшки. При этом условимся, что из одного бантика можно сделать десять рюшек, а из десяти рюшек можно сделать один бантик – ну сшить. Переписываем условие задачи: « У вас есть 22 бантика и 2 рюшки. 1 бантик и 8 рюшек вы должны отдать подружке». С бантиками всё просто – берем один и отдаем. А как быть с рюшками? Их нам явно не хватает. Посмотрим, как же мы решали эту задачу математически двумя способами. Со стороны это выглядит так.

Первый способ. Вы берете все бантики и развязываете их, разглаживаете все рюшки. Берете иголку с ниткой и сшиваете всё это в одну длинную ленту. После того, как вы закончили шить, отмеряете от ленты нужное количество и отрезаете ножничками. Торжественно вручаете офигевшей подруге кусок ленты. Потом вы с подругой режете свои ленты, делаете из них бантики и рюшки. В итоге вы с подругой, все в бантиках и рюшках, стоите, как две дуры на выданье.

Второй способ. Вы развязываете все бантики и режете их на рюшки. Делаете кучу рюшек и из этой кучи отбираете 18 штук для подружки. После этого торжественно вручаете офигевшей подружке кучку рюшек. Потом вдвоем принимаетесь разглаживать рюшки и шить из них бантики. При этом ваша подружка думает: «Во дура! Из-за этой уродины я теперь должна шить бантик». Вы же думаете: «Во дура! Из-за этой уродины я сперва резала, а теперь должна сшить аж двадцать бантиков. Больше она мне не подружка». Честно говоря, вам я не завидую.

Как видите, математически правильные способы со стороны выглядят не совсем практично. Как поступит в этой ситуации любая блондинка? Как двухядерный процессор. Возьмет один бантик из кучки бантиков и сделает из него десять рюшек. Теперь у вас есть одна кучка из двадцати одного бантика и вторая кучка из двенадцати рюшек. Из первой кучки вы берете один бантик, восемь рюшек берете из второй кучки. Вручаете счастливой подружке один бантик и восемь рюшек. Потом вы любуетесь своими сокровищами и просто трепитесь, вместо того, чтобы пыхтеть с ножницами или иголками. Это и есть третий способ решения задачи. Возвращаясь к нашим метрам и дециметрам, математически это можно записать так:

22 метра и 2 дециметра = 21 метр и 12 дециметров

(21 метр и 12 дециметров) – (1 метр и 8 дециметров) = (21 метр – 1 метр) и (12 дециметров – 8 дециметров) = 20 метров и 4 дециметра

Мы два математических действия вычитания с двумя разными единицами измерения выполняем одновременно, точно так же, как работают двухядерные процессоры Intel для компьютеров. Думаю, после такого решения в вашей тетрадке офигевать начнут математики. Хотя именно так делаются все вычисления практически. В математике принято говорить, что нужно сперва выполнить вычитание дециметров, а уже потом вычитание метров. В принципе, математики правы. Так тяжелее запутаться. При вычитании дециметров вы всегда можете слямзить один метр из метров, если дециметров вам не хватает. Потом из оставшихся метров вычитаете метры. Только не забывайте об одном метре, если вы его уже прокутили в дециметрах.

Специальная таблица для перевода единиц измерения длины из одних в другие опубликована на отдельной странице.

Найти решение:

1000 квадратных метров сколько это будет в дециметрах - это будет 100 000 (сто тысяч) квадратных дециметров. В одном метре десять дециметров, в одном квадратном метре сто квадратных дециметров (10 х 10 = 100). В нашем примере 1000 х 10 х 10 = 1000 х 100 = 100000

Таблица котангенсов от 1 до 360 градусов

Таблица котангенсов от 1 до 360 градусов. Значения котангенсов в таблице даны через один градус с точностью до десятитысячной - это четыре знака после запятой.

Котангенс нуля градусов не определен, поскольку возникает деление на ноль (это следует из определения котангенса).

Тригонометрическая функция котангенс имеет положительные значения от 1 до 89 и от 181 до 269 градусов. Для углов от 91 до 179 и от 271 до 359 градусов значения котангенса отрицательны.

Котангенс 0 (ctg 0), 180 (ctg 180), 360 (ctg 360) градусов не определен в связи с невозможностью деления на ноль. Значения котангенса 90 (ctg 90) и 270 (ctg 270) градусов равны нулю. Единице равняются значения котангенсов 45 (ctg 45) и 225 (ctg 225) градусов. Минус единице котангенс равен при 135 (ctg 135) и 315 (ctg 315) градусов.

На этом же сайте вашему вниманию предлагаются такие же таблицы тангенсов, синусов и косинусов.

Найти значение:

Котангенс 225 градусов - это ровно единичка, 1,0000, в таблице котангенсов на картинке можно найти это значение.

Катангенс 37 градусов - ctg 37 равен 1,3270.

Котангенс 1го градусов - равняется 57,2900. Удивительно, но разные люди в одинаковых фразах делают одинаковые опечатки.

ctg нуля сколько - математики говорят, "значение котангенса 0 градусов не определено" потому, что получается деление на ноль.

Таблица тангенсов от 1 до 360 градусов

Таблица тангенсов углов в градусах от 1 до 360 представляет значения тангенса в десятичных дробях с точностью до четвертой цифры после запятой (с точностью до десятитысячной). Тангенс угла таблица представляет через один градус.

Тангенс нуля градусов (tg 0) равен нулю.

Тангенс нуля градусов (tg 0) и тангенс ста восьмидесяти градусов (tg 180) равны нулю. Тангенс девяноста (tg 90) и двухсот семидесяти (tg 270) градусов не определены (по определению тангенса в этом случае получается деление на ноль). Значения тангенса 45 (tg 45) и тангенса 225 (tg 225) градусов равны 1 (единице). Тангенс 135 (tg 135) и 315 (tg 315) градусов равен -1 (минус единице).

В интервале от 1 до 89 градусов и от 181 до 269 градусов значения тангенса положительны. Значения тангенса от 91 до 179 и от 271 до 359 градусов - отрицательны. В таблице тангенсов отрицательные значения тангенса имеют знак минус.

Точно такие же таблицы котангенсов, синусов и косинусов вы найдете на других страницах сайта "Математика для блондинок".

Вы ищете:

Значения тригонометрических функций для тангенс альфа - здесь очень большая таблица тангенсов на красивой картинке. Если вам нужны тангенсы с корнями, то это на другой страничке "Тригонометрическая таблица".

Таблица косинусов от 1 до 360 градусов

Таблица косинусов в градусах от 1 до 360 градусов. Таблица значений косинуса с интервалом в 1 (один) градус. Косинус угла округлен до четырех знаков после запятой. Все углы до 360 в тригонометрической таблице даны в градусах.

Косинус нуля градусов равен единице.

Таблица косинусов с корнями растет на другой грядке, которая называется "тригонометрическая таблица". Здесь таблица косинусов приводит численные значения тригонометрической функции. Для удобства пользования таблицей, ячейки со значениями косинусов углов, кратных пяти градусам, выделены розовым цветом.

Если кому-то мало этой таблицы косинусов, можете мимоходом полюбоваться точно такой же таблицей синусов от 1 до 360 градусов. Косинусы углов от 91 до 269 градусов имеют отрицательные значения. В таблице перед значениями косинусов этих углов стоят знаки минус. Косинусы углов от 1 до 89 и от 271 до 359 градусов имеют положительные значения.

Для полного тригонометрического счастья, естественно, имеются точно такие же таблицы тангенсов и котангенсов, которые выглядят точно так же и составлены по такому же принципу от 0 до 360 градусов

Косинус 90 градусов (cos 90) и косинус 270 градусов (cos 270) имеют значения, равные 0 (нулю). Косинус 180 градусов равен -1 (минус единице).

Найти значение:

Чему равен косинус пи на 12 - косинусу 15 градусов, по таблице это 0,9659.

cos 330 градусов - это 0,866 для физиков или корень из трех деленный на два для тех, кто надеется сократить математическое выражение.

Косинус 90 градусов это сколько - это ровно ноль, есть такая симпатичная циферка 0.

Косинус угла 100 градусов - это -0,1736, не забываем значок минус перед циферками писать, ведь это значение косинуса отрицательное.

Таблица синусов от 1 до 360 градусов

Таблица синусов в градусах от 1 до 360 градусов представляет значения синуса через один градус. В таблице синусов точность значений синуса составляет четыре знака после запятой. В тригонометрической таблице синусов углы даны в градусах.

Таблица синусов начинается со значения синуса одного градуса. Синус нуля градусов равен нулю.

Таблица синусов применяется при решении самых разных математических, физических, инженерных задач. Значения синусов используются в расчетах самых разных величин в физике и других науках.

Если вам нужен синус таблица от 360 до 720, то пользоваться нужно приведенной выше таблицей синусов, предварительно пересчитав угол альфа. Если у вас угол альфа в пределах от 360 до 720 градусов, от этого угла нужно отнять 360 градусов и по таблице найти значение синуса получившегося угла. Значения синусов этих двух углов равны, поскольку в тригонометрии для синуса (и не только для него, а для всех тригонометрических функций) существует равенство:

sin (α + 360°) = sin α

В приведенной выше таблице синусов можно найти следующие значения: синус 36 градусов равен, sin 25 градусов, угол sin 27, sin угла 50 или синус 50 градусов равен. По таблице синусов очень удобно смотреть, чему равен sin 5, sin 6, sin 20 градусов. В этой же таблице можно посмотреть ответ на вопрос "Сколько будет sin 20 градусов?".

Если же вам нужно найти синус пи на 12, то поступить можно следующим образом. В тригонометрии, и не только в тригонометрии, но и во всей нашей математике, угол пи радиан равен 180 градусов. Вот эти самые 180 градусов и нужно разделить на 12, что бы найти синус пи/12. Поскольку 180/12 равно 15, то по таблице нужно посмотреть, чему равен синус 15 градусов.

sin (пи/12) = sin 15° = 0,2588

Именно на этой странице вы найдете sin таблица значений от 1 до 360 градусов. По-украински это будет звучать так: "таблиця значень тригонометричних функцій до 360 градусів". Вы не поверите, но в Украине тоже есть блондинки. И им тоже нужна математика для блондинок и тригонометрия для блондинок. Кроме всех прочих достоинств этой таблицы синусов, в ней есть sin угла 7 градусов, который многие хотят видеть.

Если вам интересно, как находить косинус синус угла 75 градусов, то это очень просто. Синус угла 75 градусов смотрите в строчечке напротив угла в 75 градусов:

sin 75° = 0,9659

Косинус угла 75 градусов смотрите в таблице косинусов, которая расположена на соседней странице.

Конечно же, без таблиц тангенсов и котангенсов от 0 до 360 градусов никакая тригонометрия не может обойтись. Во всех таблицах внешний вид одинаковый и сделаны они по одному принципу.

Найти значение:

Значение sin 50 - равняется 0,766 советую проверить по таблице - я могу ошибиться (ну подумаешь, не ту клавишу нажал).

Синус угла найти - значения синусов угла вы без труда найдете в очень красивой таблице на картинке.

Синус 15 градусов равен - 0,2588 Проверьте по таблице, я могу наврать.

Синус пи/12 - равен синусу 15 градусов. Смотрите выше.

sin 3-х градусов - равен 0,0523, если я не ошибся.

Таблица синусов по физике - для физики больше подойдет именно эта таблица. Физики - люди серьезные и в сокращение дробей не играют. Они более взрослые, чем математики.

sin 40 градусов это сколько - 0,6428 вот сколько!

Таблица факториалов до 255

Точные значения факториала натуральных чисел до 50 мы уже рассмотрели. На практике, при математических расчетах, чаще пользуются приблизительными значениями факториала, которые собраны в таблицу факториалов до 255.

Таблица факториалов

Что такое факториал? Переходите по ссылке выше, там я подробно написал о факториале. А вот на этой странице есть точное значение факториала числа 255, которое состоит из пятисот пяти (505!!!!!!) цифр. Вот такие они, страшные и ужасные факториалы.

Эта таблица нагло взята из сайта "Инженерный справочник", где вы можете скопировать точные значения факторила чисел от 1 до 255. Зачем это нужно? А вот представьте. Вы у себя в Инстаграмме (который запрещен в стране дураков под названием россия) вываливаете целый мешок цифр и с невинным видом задаете вопрос: "Угадайте, что это за число?". А потом даете скромный ответ: "Это факториал 100". Кстати, на этом же сайте есть ещё целая куча самых разных таблиц на все случаи жизни. Но не забывайте, что все люди ошибаются. На первой картинке я исправил ошибку в приблизительном значении факториала 12!. Чисто ради любопытства можете посмотреть и хорошо запомнить очень простую истину: "Никогда никому не верьте, даже себе - вы тоже можете ошибаться".

Факториал

Факториалом в математике называют произведение всех натуральных чисел, включая указанное число. Обозначается факториал восклицательным знаком после числа, например 4!. Так что, если вы встретили восклицательный знак в математике, это совсем не означает "Вау! Число!". Это просто факториал. Из священных математических текстов нужно выучить одну фразу "Факториал нуля равен единице". Почему факториал нуля равен единице? Читайте по ссылке мой фантастический опус на эту тему. Точные значения факториалов чисел до 50 приведены на рисунке.

Факториал точные значения до 50

На картинке показано, как считать факториал для натурального числа 7. Вычисление факториала других чисел производится точно так же: все числа от одного до указанного перед восклицательным знаком перемножаются между собой.

Факториал 1 (единицы) равен единице.
1! = 1
Факториал 2 (двух) равен двум.
2! = 1 · 2 = 2
Факториал 3 (трех) равен шести.
3! = 1 · 2 · 3 = 6
Факториал 4 (четырех) равняется двадцати четырем.
4! = 1 · 2 · 3 · 4 = 24
Факториал 5 равен ста двадцати.
5! = 1 · 2 · 3 · 4 · 5 = 120
Ну и так далее.

В общем виде формулу для нахождения факториала можно записать так:

n! = 1 · 2 · 3 · 4 · ... · (n - 2) · (n - 1) · n

Таблица факториалов до 255 представлена на отдельной странице.

Кстати, если вы будете ехать за рулем автомобиля и увидите восклицательный знак в треугольнике на белом или желтом фоне - это не урок математики с факториалами, это дорожный знак "Внимание!".


Здесь не нужно ничего друг на дружку умножать. Нужно отложить в сторонку косметичку, перестать болтать по мобильному телефону и крепче держаться за руль автомобиля. Внимательно смотрите не по сторонам, а на дорогу. Впереди могут быть неприятные сюрпризы. Чтобы неприятные сюрпризы на дороге не превращались в неприятные ситуации, их обозначают этим дорожным знаком.

Найти решение:

Чему равен 50 факториал - последняя строчка таблицы факториалов на картинке дает точный ответ на этот вопрос. Приблизительное значение (более короткая запись числа) можно посмотреть на отдельной странице "Таблица факториалов до 255" (ссылка выше по тексту).

Действие факториала - математически действие факториала представляет собой последовательность умножения натуральных чисел между собой. Такой себе математический междусобойчик во множестве натуральных чисел.

Факториал 15 равен - ответ можно посмотреть в таблице факториалов на картинке.

Как считать факториал - здесь в тексте написано, как считается факториал, а на картинке есть пример факториала семи (7!).

Факториал от нуля - равен единице, как бы странно это не выглядело. Но, таковы математические догмы. На картинке большими синими цифрами написано. В начале этого текста есть ссылка на мою теорию происхождения этого безобразия.

Как счетать факториал - вообще-то, у меня написано как "счИтать" факториал. Мне кажется, помимо факториалов, вам не помешает изучить курс "Русский язык для блондинок". А то не красиво будет смотреться фраза "Я табе лублу!" краской на асфальте.

Математика для блондинок факториал - это именно та страница, которую вы ищете. Если вы мне не верите, посмотрите вверху страницы, там написано "Математика для блондинок" и адрес этого сайта именно www.blondesmath.com