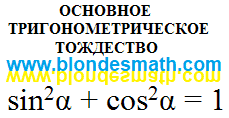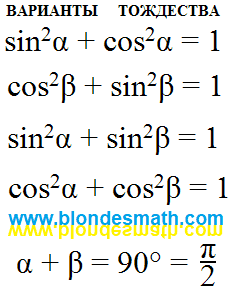Математика и карточные игры

Автор Николай Хижняк

Не помню, по какому телеканалу, смотрел рекламный ролик об одном русском математике, нашем современнике, которого не пускали в казино. Его знали уже во всех заведениях и то, что он постоянно выигрывает. Как он сам о себе рассказывал, он любил числа и легко ими оперировал. А ещё у него была отличная память. Это позволяло ему не ввязываться в игру при неблагоприятном раскладе карт и выжимать максимум из благоприятных ситуаций. Ведь любая карточная игра – это комбинаторика и математическое ожидание.

К сожалению, казино рассчитаны не на разумных существ. Там играют на животных инстинктах поиска еды и удовольствий. Ведь деньги - это и есть придуманный нами эквивалент еды и удовольствий. Зачем математик играл в казино? Если для тренировки памяти - значит он вел себя как разумное существо, воспользовавшееся сложившейся ситуацией. Если ради денег - он обычное животное, которое идет на поводу у своих инстинктов. А если он играл в карточные игры ради получения удовольствия? Кем считать математика в этом случае? Ведь от решения математических задач можно получать удовольствие, по себе знаю. И чем труднее задача, тем больше адреналина получаешь после её решения.

Наверное, все карточные игры можно отнести к разряду математических задач. Выигрыш в карточной игре можно считать правильным решением задачи. Проигрыш - не правильным решением. Перетасовку карт можно рассматривать как изменение условий задачи. Зная алгоритм решения задачи, который обычно мы называем правилами игры, мы решаем одну и ту же задачу при разных начальных условиях. Классическое математическое "Пусть нам дано..." в карточной игре превращается в определенный порядок расположения карт разного достоинства в перетасованной колоде.

Если следовать логике математиков, то карточные игры можно разделить на унарные, бинарные, тернарные, кватернарные и так далее по количеству игроков, которые принимают участие в решения карточной математической задачи (1, 2, 3, 4, и так до бесконечности). В унарных играх участие принимает один игрок (пасьянс, карточный фокус), в бинарных играх - два (игра в дурака и тому подобные игры), в тернарных - три игрока (преферанс), и так далее. На этом примере можно увидеть животную тягу математиков к умным словам. Наверное, математики получают удовольствие, когда обычные вещи называют придуманными умными словами.

С пасьянсами, думаю, всё понятно. Лучшие друзья офисных работников - это пасьянсы "Косынка", "Паук" и другие. Каждый знает правила игры и в одиночку решает математическую задачу. Всякий раз начиная игру заново, вы получаете новые условия задачи. А что такое карточные фокусы? Это когда фокусник показывает решение математической задачи людям, которые не знают алгоритм решения. Зрители видят только начальные условия (колоду карт) и результат решения задачи. Сам ход решения математической задачи с картами им остается не доступным.

Вот так хитрые обезьяны и ловят на колоду карт жадных (в казино) или любопытных (фокусы) обезьян. Зачем они это делают? Ради корма (денег), для себя, любимых :)

Квантовая механика

Автор: Сергей Манулов

Решил немного приобщиться к квантовой механике, для этого открыл книжку Савельев «Курс общей физики Том. 3.» Очень заинтересовал параграф 19: «необычные свойства микрочастиц». Там говорится о том, что микрочастицы обладают рядом специфических необычных свойств. Автор даже пишет, что возможно их правильнее называть частицами-волнами. Савельев цитирует Феймановские лекции, мне лично очень не понравился их посыл.

Цитата: «Раз поведение атомов так не похожи на наш обыденный опыт, то к нему очень трудно привыкнуть. И новичку в науке, и опытному физику – всем оно кажется своеобразным и туманным.» С этим трудно поспорить. А вот дальше: «Даже большие учёные не понимают его настолько, как им хотелось бы, и это совершенно естественно, потому что весь непосредственный опыт человека, вся его интуиция – все прилагается к крупным телам. Мы знаем, что будет с большим предметом, но именно так мельчайшие тельца не поступают. Поэтому, изучая их, приходиться прибегать к различного рода абстракциям, напрягать воображение и не пытаться связывать их с нашим непосредственным опытом.»

Мягко говоря, тут логический парадокс. Человеческое сознание, его абстракции основаны на опыте, никак иначе. Любые фантазии имеют опытную подоплёку. Которая, в свою очередь, основана на опыте изучения крупных тел, что нам привычны.

Но автор пишет дальше: «Всякая наглядная модель неизбежно будет действовать по классическим законам и поэтому не пригодна для представления квантовых процессов. Поэтому надо отказаться от наглядности. Отсутствие наглядности поначалу может вызывать чувство неудовлетворенности, но со временем это чувство проходит, и все становится на свои места.»

Лично я вижу в этом абзаце, огромный простор для спекуляций. Нет наглядности, а значит можно теперь любой бред представить за правду.

«Сочетая в себе свойства частицы и волны, микротела «не ведут себя ни как волны, ни как частицы…». Отличие микрочастицы от волны заключается в том, что она всегда обнаруживается как неделимое целое. Никто никогда не наблюдал, например пол электрона.»

Согласно современным представлениям физики элементарных частиц, электрон неделим и бесструктурен. Но я уверен, пройдёт время и люди откроют частицы, из которых состоит электрон.

«В то же время волну можно разделить на части и воспринимать затем каждую часть в отдельности. Отличие микрочастицы от привычной нам макрочастицы заключается в том, что она не обладает одновременно определенными значениями координаты и импульса, в следствии чего понятие траектории применительно к микрочастицам утрачивает смысл.»

-Ты видишь суслика?
-Нет.
-А он есть (С) ДМБ.

То что мы не видим или не можем определить, ещё не означает того, что оно не существует, но и не означает, что это существует.

Далее приводится мысленный эксперимент, если вкратце: даны два узеньких отверстия, на движение электрона влияет каждое из отверстий. Если бы электрон в каждый момент времени находился в определенной точке пространства и двигался по траектории, он проходил бы через определенное отверстие – первое или второе. Но там произошла дифракция, что доказывает, что в прохождении каждого электрона участвуют оба отверстия – и первое и второе.

«Не следует, однако, представлять дело так, что какая-то часть электрона проходит через одно отверстие, а другая часть через второе. Электрон всегда обнаруживается как целое, с присущей ему массой, зарядом и другими характеристиками. Обычный шарик, даже очень малых размеров, не может быть прообразом микрочастицы, всё сложнее.»

Спрашивается, тогда как это происходит? Как такое возможно? Что электрон проходит через оба отверстия как волна, но он при этом не делим?

На мой взгляд, исходя, из моего жизненного опыта природа устроена так, что все процессы повторяются, но сама их форма изменяется. Сущность явления образно одинаковая, а вот сам её процесс другой. Квантовые частицы должны действовать подобно макрочастицам, но по-другому, своеобразно. Единственное объяснение, как электрон так проходит, является образ сита и воды. Автор говорит нельзя делать образы и аналогии с макромиром в квантовой механике. Лично на мой субъективный взгляд это неверное. Природа самоподобна. В ней есть строгие качественные и количественные закономерности.

Вот моя аналогия: капелька воды капает на сито, она с него стекает, образуя каплю. Энергетика электрона, её постоянные физические величины можно представить как плотность. У воды это величина постоянная при одних и тех же условиях. Так почему бы и у электронов не может быть такая вот «плотность»? Получается, что электрон он «вязкий», как слизняк. А ведь это применимо и к другим частицам.

Когда электрон размазывается, каждый его участок будет иметь одинаковую энергию и свойства. Но эти участки могут отличаться друг от друга неким параметром который либо ещё неоткрыт (не выдуман) либо им пренебрегают.

Такая аналогия подтолкнула меня к мысли о «слизняковом» или «улиточном» перемещении материи.

Представьте себе молекулу водорода: 1 большой протончик, вокруг него носится электрон. Попробуем его сдвинуть, сообщая кинетическую энергию. По моей гипотезе или предположению, движение будет происходить за счёт расширения, а затем сокращение формы протона и электрона, на одинаковую величину. Как улитка. Она сначала расширяет свой перед, затем, свой зад втягивает к переду, тем самым перемещается. Как резинка, возьмём её натянем, затем один конец отпустим, она переместится к другому. Такое движение идёт на определённое расстояние в зависимости от энергии. Оно квантуется, то есть сокращение идёт порциями. Есть определённый предел, растяжения, больше которого микрочастица не может растянуться. Если его всё-таки превысит, частица может уничтожиться. При этом растяжении все свойства физической частицы в каждой её области остаются неизменны, кроме некоторых неизвестных или пренебрегаемых сейчас параметров. Ведь согласно преобразования Лоренца, при движении длина объекта увеличивается в направлении движения. Тут нечто похожее.

Чем больше сообщено кинетической энергии, тем больше микрочастица совершает сокращений. Эти сокращения могут быть настолько незначительными, что ни один прибор их никогда не уловит. Эффект похож на размытие движения при съёмках на фотоаппарат. Только он им не является.

Если подытожить: то микрочастицы можно рассматривать как вязкие капли, это условно, они не являются каплями, но ведут себя похожим образом. Капля воды в невесомости приобретает форму сферы. Примерно так же выглядят и микрочастицы (протоны, нейтроны, электроны….). И ведут себя они схоже. Мне кажется, что они так же образованы мельчайшими частицами, которым ещё очень долгое время, либо никогда, не удастся найти человеку. Любая волна на макрауровне – это результат перемещения огромного количество различных частиц. В микромире всё должно быть схоже.

Основное тригонометрическое тождество

Заглянул в Википедию и посмотрел, что такое основное тригонометрическое тождество. Картинку из раздела Википедии "Тригонометрия" я уже приводил. На специальной странице в Википедии, посвященной основному тригонометрическому тождеству, информации не на много больше: приведено само тождество и добавлено несколько строк пояснений.

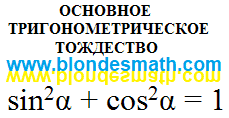Основное тригонометрическое тождество

В частности, указывается, что иностранцы называют это тригонометрическим тождеством Пифагора или просто теоремой Пифагора. И это всё?! Да уж, не густо. Усаживайтесь по удобнее, разговор у нас будет длинным и нудным, но, думаю, он того стоит.

Я уже говорил, что иностранные математики лучше понимают тригонометрические функции, но и у них не всё так гладко. Вот их картинки.

Основное тригонометрическое тождество

Основное тригонометрическое тождество

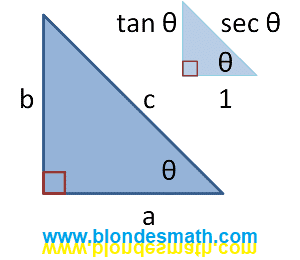
Обратите внимание на последнюю картинку. Теорему Пифагора они представляют через тангенс и секанс и показывают это на треугольнике. Формулы тригонометрического тождества в этом случае приобретают следующий вид:

Основное тригонометрическое тождество

Как видите, единица плюс квадрат тангенса угла равен квадрату секанса этого же угла, единица плюс квадрат котангенса угла равен квадрату косеканса этого угла. Очень интересные формулы, в будущем мы к ним вернемся. Есть там и робкая попытка выполнить преобразования тригонометрических функций. Но, наверное, они сами испугались своих действий, ведь полученные формулы необходимо будет объяснять. С точки зрения классического определения тригонометрических функций через отношение координат точек окружности - это задача не из легких.

Основное тригонометрическое тождество

В низу картинки приведена констатация того факта, что теорема Пифагора, она же основное тригонометрическое тождество, не зависит от направления измерения угла.

Теперь давайте и мы выполним преобразования тригонометрических функций синуса и косинуса. Используем следующие формулы:

Преобразования тригонометрических функций

Обращаю ваше внимание, что в данном случае снова срабатывает принцип "минус на минус дает плюс", только для правила прямого угла: если мы одновременно поменяем угол и название тригонометрической функции, результат останется неизменным. У всех подобных преобразований есть один общий "родитель" - зеркальная симметрия. Любое зеркальное отображение, выполненное дважды, возвращает нас к первоначальному результату. Не зависимо от того, что мы отражаем. Отсюда можно сделать вывод, что все преобразования тригонометрических зависимостей зеркально симметричны преобразованиям углов.

Запишем результаты преобразований в виде основных тригонометрических тождеств:

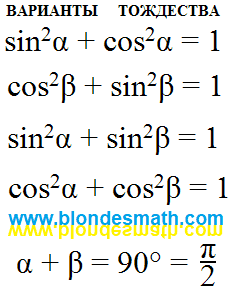Основное тригонометрическое тождество

В первой строчке, для сравнения, тождество представлено в классическом виде. Если эти тождества выполняются, значит два угла альфа и бета образуют прямой угол. И наоборот, если два угла образуют прямой угол, для них всегда будут выполняться основные тригонометрические тождества. Естественно, возникает вопрос, о каких двух углах идет речь, если классическое определение тригонометрических функций всегда говорит об одном угле между осью икс и единичным отрезком? Думаю, именно это обстоятельство испугало иностранных математиков и не привело их к показанным выше формулам.

Оставим классическое определение на совести математиков, рассмотрим прямоугольный треугольник. Как выглядит типичная формулировка математиков? "Пусть нам дан прямоугольный треугольник. Обозначим угол этого треугольника через альфа..." Вот здесь и возникает первый вопрос: какой именно угол треугольника мы обозначаем через альфа? У треугольника углов аж три штуки. Очень часто математики обозначают буквой альфа именно тот угол, который им нужен в данный момент. Это приводит к тому, что в разных формулах принципиально разные вещи имеют одинаковое обозначение. Потом математики начинают это обобщать и сваливают всё в одну кучу, в которой что-либо понять уже просто невозможно, остается только верить определению.

Обозначать прямой угол в прямоугольном треугольнике не принято. Буквой альфа обозначается один из двух острых углов. Какой именно? Не имеет значения. Теорема Пифагора выполняется как для одного угла, так и для второго. Точно так же для двух острых углов можно определить тригонометрические зависимости. Это проявление относительности тригонометрических функций. Так вот, если мы один острый угол прямоугольного треугольника обозначим через альфа, то углом бета будет второй острый угол. Для двух этих углов записаны наши четыре варианта тригонометрического тождества.

Как же быть с классическим определением тригонометрических функций через координаты точки на единичной окружности? Здесь то же нет особых проблем, если за аналог брать треугольник. Давайте рассмотрим все четыре варианта записи тригонометрического тождества на картинках. Возьмем традиционный тригонометрический круг с радиусом, равным единице и точно такой же прямоугольный треугольник с гипотенузой, равной единице. Для наглядности, поместим треугольник в систему координат. Вот классический вариант, когда сумма квадратов синуса и косинуса угла альфа равняется единице.

Преобразования тригонометрических функций

Красным цветом на рисунке выделены особенно важные моменты, на которые нужно обратить внимание. Для перехода от угла альфа к углу бета в тригонометрическом тождестве, нужно принять ряд правил, на которые обычно никто не обращает внимания и которые мы будем считать неизменными:

- косинусом угла является проекция единичного элемента (отрезка или гипотенузы) на ось икс, синусом - проекция на ось игрек;
- начало отсчета угла совпадает с осью икс;
- вершина угла совпадает с точкой ноль системы координат;
- положительное направление отсчета угла совпадает с первой четвертью системы координат, в которой синусы и косинусы положительны.

Математика - это относительность. Мы можем рассматривать неподвижную (стационарную) систему координат с подвижными (динамичными) объектами (отрезком и треугольником), можем неподвижные (стационарные) объекты рассматривать в подвижной (динамичной) системе координат. Результаты будут одинаковыми.

В математике чаще всего используют стационарные системы координат. В жизни каждый из вас пользовался физическим аналогом динамической системы координат - линейкой. При определении периметра многоугольника, нарисованного на бумаге, у вас есть два варианта действий: держать линейку неподвижно и вращать листок с многоугольником, либо оставить листок неподвижным и вращать линейку, измеряя каждую сторону. В первом случае вы пользуетесь стационарной системой координат, во втором - динамичной. В любом случае это даст вам возможность измерить все стороны многоугольника. Вы выбираете ту систему координат, с которой вам удобнее работать. Вы всегда берете с собой линейку и идете с ней в школу, а не наоборот.

В нашем тригонометрическом тождестве мы применим оба метода. Стационарный единичный отрезок мы рассмотрим в динамичной системе координат. При этом нам необходимо будет выделить две системы координат - для угла альфа (её мы обозначим икс альфа и игрек альфа) и для угла бета (икс бета и игрек бета). Динамичный треугольник мы рассмотрим в стационарной системе координат. Для перехода от угла альфа к углу бета нам нужно повернуть треугольник на 90 градусов против часовой стрелки и отразить его зеркально. Этот процесс показан на рисунке ниже. Для наглядности, все обозначения треугольника преобразуются вместе с ним.

Поворот треугольника

Теперь рассмотрим основное тригонометрическое тождество для угла бета. Для единичного отрезка оси икс и игрек в этом случае меняются местами, угол бета отсчитывается против часовой стрелки.

Преобразование тригонометрических функций

Для тригонометрического тождества в виде квадратов синусов углов альфа и бета в случае единичного отрезка разным углам соответствуют разные системы координат. В случае треугольника синусам разных углов соответствуют разные катеты. Сложение величин, расположенных в разных системах координат, не противоречит правилам математики. Главное, что бы единицы измерения в разных системах координат были одинаковыми. Каждую динамичную систему координат можно рассматривать как последовательный переход от одной стационарной системы координат к другой на разных этапах выполнения математических действий.

Применение динамической системы координат упрощает математическое описание процесса. Например, так мы описываем вычисление периметра многоугольника - сложение отрезков, расположенных под разными углами - без применения средств векторной алгебры или тригонометрических функций. Правила перехода от одной системы координат к другой для разных математических действий могут быть разными. Для тригонометрических функций поворот системы координат на прямой угол приводит к изменению названия этих функций по правилу прямого угла, при условии неизменности всех прочих правил. Выше я специально подчеркивал это, поскольку изменение правил может привести к изменению результатов математических действий.

Преобразование тригонометрических функций

Если тригонометрическое тождество выразить через косинусы, ситуация получается аналогичной синусам, но рассматриваются проекции на другие оси координат или в треугольнике берутся другие катеты.

Преобразование тригонометрических функций

Подставляя в полученные формулы вместо единицы другие варианты этого же тождества, мы можем записать тригонометрическое тождество для двух углов:

Основное тригонометрическое тождество

Выполняться эти тождества будут только в том случае, если сумма углов равняется прямому углу. Если тождество не выполняется, тогда необходимо переходить к форме записи тригонометрического тождества с нейтральными элементами и искать, какой из нейтральных элементов перестал быть нейтральным и начал вносить свои поправки в существовавшее до этого равенство. Тригонометрические тождества с нейтральными элементами записаны с соблюдением симметрии относительно знака равенства.

Основное тригонометрическое тождество

Как один из вариантов трактовки нейтральных элементов, приведены значения синуса и косинуса прямых углов. Но на практике нейтральный элемент может скрывать любое математическое выражение, имеющее соответствующее значение при данных условиях. Например, основное тригонометрическое тождество перестанет выполняется, если прямой угол в прямоугольном треугольнике перестанет быть прямым (сумма двух углов альфа и бета не равна 90 градусов). То есть, если мы от прямоугольного треугольника перейдем к треугольнику обычному. Для классического определения тригонометрических функций это обстоятельство можно трактовать как переход от прямоугольной декартовой системы координат к косоугольной аффинной системе координат.

Другим примером может служить переход от двухмерного пространства к многомерному. Если единичный отрезок выходит из плоскости двухмерной евклидовой системы координат, тогда тригонометрическое тождество в этой системе перестает выполняться. Единице будет равняться сумма квадратов проекций единичного отрезка на оси координат многомерной прямоугольной системы. В тригонометрической форме проекции будут выражаться через синусы или косинусы углов между единичным отрезком и соответствующей осью координат. Основное тригонометрическое тождество для многомерного пространства можно записать в таком виде (это один из вариантов):

Основное тригонометрическое тождество

Поскольку все математические формулы и равенства сводятся к одному из основных математических равенств, то теоретически все математические формулы можно представить в тригонометрическом виде и увязать между собой в единую замкнутую систему. Изменяя отдельные условия, будет осуществляется последовательный переход от одних формул к другим. Восстановление первоначальных условий приведет к первоначальному математическому выражению - начальной формуле. Эти превращения не должны зависеть от того, с какой именно формулы начинаются превращения. При этом необходимо помнить, что чем больше внешних факторов мы рассматриваем, тем сложнее математическое описание.

В следующий раз мы рассмотрим, как осуществляется переход от тригонометрической формы записи теоремы Пифагора к традиционной и что это означает.

Синус на синус, косинус на косинус

Решаем очередную задачу по тригонометрии. Здесь есть синус на синус и косинус на косинус. Вот только углы разные у одинаковых тригонометрических функций.

cos62*cos28-sin62*sin28

Начнем с анализа ситуации. Если бы подобную задачку на подкинула Природа, думать особо нечего - Природа очень умная, но не хитрая. Поскольку задача находится в учебнике, значит её придумал человек. А люди очень коварные существа, всю жизнь пытаются кого-то перехитрить. Вот и здесь. Углы у нас даны в градусах. Посмотрим на сумму этих углов - они равна 90 градусов. Не спроста всё это. За этим грозным тригонометрическим выражением явно кроется что-то более простое.

Используем заморские знания о преобразовании тригонометрических функций и приведем все наши синусы и косинусы к одному углу, а потом посмотрим, что из этого получилось. Один косинус превращаем в синус, один синус превращаем в косинус. В результате у нас получились тригонометрические функции с одинаковым углом. Здесь не имеет значения, к какому углу мы придем в итоге - к углу в 28 градусов или к углу 62 градуса, результат будет одинаковым.

Синус на синус, косинус на косинус

Вот теперь у нас получилось что-то более понятное. Дальше вспоминаем первый класс - от перестановки сомножителей произведение не меняется. После этого вспоминаем детский садик - если у нас что-то отнять, мы расплачемся, потому что у нас ничего не останется. Как раз наш случай. В математике это "ничего" обозначается цифрой ноль. Вот этот ноль и был спрятан за таким страшным тригонометрическим выражением.

Пятиклассница открыла новое химическое вещество

Десятилетняя американская школьница Клэр Лэйзен (Clara Lazen), учащаяся пятого класса из города Канзас-сити, открыла новое химическое вещество - ранее неизвестную молекулярную структуру. Сделала она это случайно на уроке химии. Нужно отметить, что школа эта не простая, а работает по специальной методике, разработанной Марией Монтессори.

На одном из уроков ученикам дали задание собрать модели атомов из специального конструктора. В нем цветные шарики-"атомы" соединялись пластиковыми палочками, обозначавшими химические связи. Клэр соорудила конструкцию из "атомов" углерода, кислорода и азота. Учителю Кеннету Беру эта конструкция показалась очень странной. Он сфотографировал эту конструкцию и отослал фото по Интернету профессору химии из университета Бобу Зеллнеру, своему приятелю.

Профессор не знал, известно химикам это вещество или нет. Он занялся изучением научных работ по химии, начиная с 1904 года. В одной статье упоминалось подобное вещество - тетранитратоксикарбон, но структура расположения атомов в нем была другая, следовательно и свойства этого химического вещества были другие. Профессор Зеллнер исследовал структуру нового вещества при помощи компьютерного моделирования и сделал заключение, что его можно использовать для сохранения энергии. Скорее всего, пятиклассница изобрела новый тип взрывчатки или что-то ещё.

Статья профессора о новом веществе, соавторам которой Клэр Лэйзен стала в десять лет, появилась в научном журнале. Зеллнер надеется, что девочка не потеряет интерес к науке. По его признанию, девушки зачатую лучше подготовлены к обучению в высших учебных заведениях, чем юноши, но впоследствии они не стремятся заниматься научной деятельностью.

По материалам РИА Новости, видео и статья на английском Fox 4 News.

Гравитация

Размышления Сергея Манулова на тему гравитации.


Когда проходят в школах и институтах строение молекул и атомов, то почему не затрагивают гравитационное воздействие между ними? Вопрос риторический. Но вот насколько я понимаю, то сила связывающая ядро и электроны – электромагнитная. Сила, связывающая ядра – сильное взаимодействие (которое тоже аналогично электромагнитному?).

У меня есть предположение – догадка, что вселенная самоподобна, то есть принципы и свойства одинаковы и схожи на всех уровнях, что на микро, что на макро. Сменяется лишь качественная характеристика этого подобия. Как в химии, одни и те же элементарные частицы, а сколько свойств! Количество электронов и заряда атомных ядер переходят во все новые качества. Но свойства их сохраняются в определённой зависимости, что выражается периодическим законом.

Так вот, вчера я задумался о гравитации. Поскольку, когда рассматривают атомы и электроны, почему-то мало говорят или не говорят вовсе о гравитации и их влиянии, то у меня сложилось мнение что гравитационная сила слабее электромагнитной?

Тогда я начал рассуждать, что может быть гравитацией? Используя принцип аналогии, мне пришла в голову идея, что ядра атомов есть источник гравитационного поля.

Вообще, удивительно и то, что сами ядра свойственны природе на различных уровнях.

Ядра в атомах, ядра в клетках, ядра в орехах, ядра в планетах, ядра в галактиках… Вот это я называю самоподобием, повторением некоторых структурных свойств материи, на определённых качественных уровнях. Отсюда и теория струн, которая описывает уровень, где материя выглядит как струны :) Возвращаясь к своей гипотезе, что ядра есть носители гравитации. Я начал думать как это можно изобразить.

Я представил ядра как некий объект имеющий + и - . Этот + и – индуцируется в присутствии других ядер и сориентируется таким образом, чтобы + становился к минусу другого ядра, а минус к плюсу. По аналогии с электростатикой. Ядро же вроде хаотично вращается? Тогда + и – при индицировании будет выражаться среднестатистическим положением ядра, при этом + будет чаще всего там где напротив него -. Эти «заряды» могут быть и не зарядами, а чем-то другим. Их энергия намного меньше электромагнитных сил, и ещё меньше сильного взаимодействия. Но они становятся весомыми при большой совокупности молекул.

Возьмём планету, пусть Земля. Внутри Земли ядро, затем магма, земная кора, гидросфера, суша, атмосфера. По логике вещей, и следуя принципу минимальной энергии. Химические вещества будут ложиться на Землю, если они имеют индуцированные заряды, + к минусу, а минус к плюсу. И так получается очень толстенькая оболочка. Это притягивает ядра. Сами же ядра будут ещё склеиваться гравитационным воздействие, которое намного слабее электромагнитного. Но при этом оно не зависит от электромагнитного. Поэтому будут удерживаться и неполярные молекулы (а ля водород или инертные газы), но слабее, чем более тяжёлые их сородичи.

Сами же ядра будут ориентироваться вышеописанным образом. Если мы механически поднимем молекулу с этим ядром, ядро переориентируется таким образом (подобно гироскопу), чтобы его + и – оставались в исходном положении. Вот это и будет гравитационной силой.

Далее, используя принцип аналогии, становится понятным почему у Земли горячее ядро. Лантаноидное сжатие! Чем больше электронов на f, тем меньше радиус (грубо говоря), тем сильнее давление на ядро? Тоже самое и для гравитации. Чем больше радиус объекта, тем сильнее давление на его ядро, тем сильнее оно разогревается, энергии много сообщается. Гравитационная сила самая слабая на микроуровне, но в совокупности на макро – самая сильная, поскольку электромагнитная и сильное взаимодействия они скомпенсированы и приблизительно равны нулю. И вот с нарастанием гравитационной силы, она начинает воздействовать на электромагнитные и сильные взаимодействия. Начинаются ядерные реакции. Уверен внутри Земли существуют сверхтяжёлые элементы. А на солнце в ядре ещё более сверхтяжёлые. А в чёрных дырах абсолютно тяжёлые. Но я думаю, есть предел образования сверхтяжёлых элементов, после которого происходит взрыв. Он описывается ещё неким фактором, который мы не знаем.

Что касается обычного ядерного распада, то там всё по проще. Как известно, у водорода, азота и так далее период полураспада стремится в бесконечность (или до ужаса огромен). Но он существует - радиоактивная вода. Тяжёлая вода. В ней уже нарушился баланс. Смысл в том, что электроны оптимально рассчитаны на определенный состав ядра. Когда состав отличается, энергетика вещества сильно изменяется, происходит дисбаланс, в результате вещество распадается.

Сверхтяжёлые элементы, 100-113 имеют плохое строение в плане энергетической выгоды, оттого распадаются. А вот дальше должны найтись вещества с хорошим и выгодным строением, для продолжительного периода существования.

Мне так же кажется, что в чёрной дыре существует не только ядерное, физическое, гравитационное взаимодействие, но и химическое. У этого сверхтяжелейшего вещества внутри чёрной дыры должно быть огромнейшее координационное число. Это некий металл, суперщелочной. Но это химическое взаимодействие затрудняется гравитационной силой.

Так же стоит отметить, что гравитация тем сильнее чем больше масса ядра или совокупности веществ.

Это лишь маленькая догадка. Что думаете по этому поводу?

Синус двух арксинусов

Ещё один пример на жонглирование тригонометрическими формулами. На этот раз попался синус двух арксинусов. При выполнении разных трюков на арене математического цирка нужно помнить, что ваши дрессировщики не заставят вас выполнять те трюки, которых вы не знаете. Нужно применять всё то, чему вас уже научили, начиная с первых классов. Вот пример.

Синус двух арксинусов

Синус арксинуса находится очень быстро - отбрасываем буковки и задача решена. В результате должно остаться просто число или математическое выражение, которое превращается в число. Но в данном случае между синусом и арксинусом стоит число, которое не дает нам тупо выбросить названия функций. В тригонометрии есть формулы двойного угла, вот эту формулу для синуса мы и применим.

Как видим, в результате двойка вылезла из синуса и умостилась впереди нашего выражения. Но в математике не бывает всё так просто. Противная двойка вместо себя оставила нам на память сразу две тригонометрические функции - синус и косинус. С синусом теперь никаких проблем нет - он благополучно уничтожается арксинусом. А вот с косинусом проблемы - внутри него появился всё тот же арксинус. Разные названия тригонометрических функций с арком и без говорят о том, что так просто от них не удастся избавиться.

Есть в математике формулы, которые позволяют перегнать математических зверей из клеток с одними названиями в клетки с другими названиями. Вот такой вот математический зоопарк. И нам в принципе не важно, кого куда загонять - косинус в синус или арксинус в арккосинус. Если мы выполним одну из этих операций, мы получим необходимый результат - оба зверя окажутся в одной клетке. Если мы выполним сразу две эти операции, мы снова окажемся в дураках: косинус арксинуса поменяется на синус арккосинуса - оба зверя по-прежнему будут в разных клетках, только других.

Вам эта ситуация ничего не напоминает? Плюс на минус дает минус, минус на минус дает плюс. Мне кажется, очень похоже. И в том и в другом случае главным является результат. Если мы что-то делаем один раз (умножаем на минус или применяем одну из формул), то результат меняется. Если мы что-то делаем два раза (дважды умножаем на минус или применяем сразу две формулы), то результат не меняется. В случае со знаком числа он так и остается неизменным, в случае с названиями тригонометрических функций - они меняются местами. Это уже фокусы математической симметрии. Как видите, математика - это не просто тупое жонглирование числами или формулами, это ещё и математические принципы решения различных математических задач. Если мы сделаем то или это - получим нужный результат. Если мы сделаем и то, и это - ничё не получим, или получим совсем не то, что нам надо. В математике всё очень просто: два раза соври - получится правда. Это касается любых решений любых задач. Один раз вы врёте, когда допускаете ошибку в ходе решения задачи, второй раз вы врёте, когда подгоняете это решение под заранее известный результат. Лично мне кажется, что почти вся современная математика держится именно на этом принципе. Но это так, лирическое отступление.

Косинус мы трогать не будем, пусть отдыхает. Преобразуем арксинус в арккосинус. Для преобразования арксинуса в любую другую арканутую тригонометрическую функцию есть специальные формулы. В нашем примере число больше нуля но меньше единицы. Используем первую формулу для арксинуса.

Формулы преобразования арксинуса

Кстати, при подготовке решения этой задачи я допустил грубую ошибку и использовал формулу преобразования арккосинуса в арксинус, для чего даже предварительно опубликовал формулы преобразования арккосинусов. Но ни переделывать решение задачи, ни врать второй раз мне не пришлось. От неминуемой смерти меня спасла симметрия тригонометрических функций синус и косинус. Интересно, почему при описании свойств тригонометрических функций математики упорно молчат об этой симметрии? Либо они считают всех дураками, не достойными столь высоких математических знаний, либо сами ничего не понимают в тригонометрии. В математике "знать" и "понимать" - это разные вещи. Говорящие попугаи то же могут знать очень много умных слов, но они ничего не понимают в сказанном.

Таким образом, мы добились того, что наш косинус вместе с арккосинусом бесследно исчезают из нашего уравнения. Дальше мы просто гоняем циферки, выполняя простое математические действия с числами. Как видите, ответ можно получить без всякого калькулятора. Можно просто тупо взять калькулятор и посчитать на калькуляторе без всяких формул. Для проверки полученного результата я так и сделал.

Формулы преобразования арккосинуса

При решении разных задачек из учебников, иногда вам могут пригодиться формулы преобразования арккосинусов в другие арканутые тригонометрические функции.

Формулы преобразования арккосинуса

По этим формулам можно преобразовать арккосинус со знаком минус в арккосинус без минуса, а так же в арксинус, арктангенс, арккотангенс без числа два впереди и с числом два впереди на лихом коне.

Вместо значка "икс" в этих формулах можно подставлять любые числа или математические выражения из тех, которые математики придумали для своих задачек.

Арккосинус синуса

Тут меня попросили решить примерчик - найти арккосинус синуса:

7/пи*arccos(sin(-пи/7)) - надо посчитать без калькулятора и таблицы))

Честно скажу, чувствую себя обезьяной, которую вытащили на арену цирка и просят продемонстрировать трюк. Но я умная обезьяна - сразу делать ничего не буду. И вам не советую. Усаживаемся поудобнее на арене, смотрим в пример и с умным видом начинаем разводить философию.

В жизни вам такое вряд ли встретится. Значит это дело рук человеческих. Очень похоже на хорошо закрученную интригу при дворе царя людоедов. Об этом свидетельствует дубинка знака минус, скромненько завернутая в круглые скобки. Если эту дубинку где-то случайно уронить, через неё можно споткнуться. В этом случае учитель вас точно съест, притом живьем и без соли. Анализируем дальше.

Арккосинус - это угол по числу. То есть, мы берем число и при помощи арккосинуса получаем из него угол. Синус - это число по углу. Вот если бы у нас был косинус, тогда бы он очень чудненько взаимоуничтожился с арккосинусом. Физики подобный процесс называют аннигиляцией, он сопровождается выделением энергии. Поскольку у нас математика, аннигиляция арккосинуса и косинуса происходит без выделения умственной энергии - просто берем эти буковки и выбрасываем их в мусор. Остается голый угол в своем первозданном виде.

Теперь наша задача состоит в том, что бы превратить синус в косинус. Попытки отыскать необходимое снадобье у местных знахарей математики на страницах русскоязычной Википедии закончились неудачей. Пришлось обращаться к знаниям знахарей заморских. У меня складывается такое впечатление, что они гораздо ближе к пониманию смысла тригонометрии, чем наши доморощенные "мудрецы". Вот заморские рецепты.

Преобразования тригонометрических функций

Первая строчка этой таблицы - это именно то, что нам нужно.

Проведенные мною археологические раскопки показали, что в более древних манускриптах знахарей от математики функция арккосинус считалась бесконечнозначной в связи с периодичностью тригонометрических функций. В более поздних творениях подобное утверждение отсутствует. То ли писцы при переписывании рукописей этот факт пропустили, то ли знахари поумнели... Но рекомендую вам уточнить это обстоятельство в тех учебниках, по которым учат вас. Я же буду считать, что арккосинус имеет только одно значение. Баба с воза...

Ну и последняя философская мысль при созерцании примера. Глядя на числители и знаменатели углов, которые подозрительно похожи по значению и помня о том, что этот пример придумали люди, я подозреваю, что у нас что-то с чем-то должно сократиться. Всё, философские размышления закончены, можно приступать к исполнению трюка:

(7/пи)*arccos(sin(-пи/7)) = (7/пи)*arccos(cos[(пи/2)-(-пи/7)]) = (7/пи)*arccos(cos[(пи/2)+пи/7]) = (7/пи)*[(пи/2)+пи/7] = (7/пи)*[(7пи+2пи)/14] = 7*9пи/(пи*14) = 9/2 = 4,5

Судя по ответу, это как раз подходит под условие "посчитать без калькулятора и таблицы" арккосинус синуса.