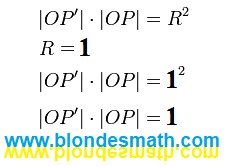Система уравнений квадраты и кубы

В ответ на "плиз" в комментариях решаю систему уравнений с квадратами и кубами возле иксов и игреков. Честно признаюсь, не люблю я в этой фигне ковыряться. Каждое решение состоит из двух независимых элементов: собственно математики и бюрократических правил оформления решения. Если математика не подвластна ни людям, ни богам, то бюрократические правила зависят исключительно от прихотей бюрократов. Каждый руководитель бюрократической системы считает своим долгом изменить существующие бюрократические правила, тем самым вписать свое имя в историю науки. Но... Бюрократы приходят и уходят, а наука остается наукой.

Я уже очень давно сбежал из мест дрессировки обезьян - школы, техникума, института... А посему существующих правил записи решения я не знаю. Да и каждый учитель волен выдумывать свои собственные правила. А по сему свое решение я запишу так, как умею, и дам некоторые пояснения.

Система уравнений квадраты и кубы

Оба уравнения системы имеют одинаковый элемент, который можно выделить - это икс в квадрате умноженный на игрек в квадрате. Заменим его на элемент "а". Перепишем заново нашу систему уравнений. Многоэтажные показатели степени возле икса и игрека исчезли, а это уже обнадеживает.

Из второго уравнения выразим наше "а" через икс и подставим это значение в первое уравнение. У нас получилось, что игрек относится к иксу как восемь, то есть в одном игреке от нас спрятали восемь иксов. Возвращаемся к уравнению "а" и вместо игрека подставляем его значение в восемь икс. У нас получается, что "а" равняется шестидесяти четырем иксам в четвертой степени.

Возвращаемся к той системе уравнений, где у нас "а" умноженное на игрек равняется шестнадцати, а "а" умноженное на икс равняется двум. Из второго уравнения мы без труда находим значение икс. Главное, правильно выковырять корень пятой степени. Но, составители системы уравнений особым садизмом не отличаются, а потому нам это удается без труда, представив число тридцать два как двойку в пятой степени. Дальше значение икса подставляем в первое уравнение и находим значение игрека.

Я не знаю, можно так решать уравнения или "низзззя", но проверка в конце показывает, что я нашел правильные значения икса и игрека.

Тангенс пи с наворотами

Рассмотрим задачу по нахождению значения тангенса пи с наворотами. Попробуем найти тангенс 38/3 пи. Почему я говорю, что этот тангенс пи с наворотами? Углы математики считатю точно так же, как собака гоняется за своим хвостом. В этом ролике собака повернулась на угол не менее 74 пи. Полный оборот составляет 2 пи, а в нашей задаче угол равен 38/3 пи. Шесть раз математики вокруг своей оси обернулись прежде, чем угомонились. Лично я воспринимаю это только так.

Но приступим к решению задачи. Для начала, поступим очень просто - возьмем калькулятор и посчитаем.

При общении с любым калькулятором на тему углов, прежде всего, необходимо уточнить, на каком языке вы собираетесь разговаривать - на языке градусов или на языке радиан. От этого будет зависеть правильность полученного результата. В любом калькуляторе есть переключатель единиц измерения углов. В нашем калькуляторе он расположен в верхнем правом углу. Тыкаем мышкой в пыптик радиан, он должен засветиться от счастья зеленым цветом. Потом мы должны указать калькулятору, о какой именно тригонометрической функции мы будем вести свою умную беседу. В нашем случае мы собираемся говорить о тангенсах, а по сему нажимаем кнопочку tg или tan. Наш калькулятор импортный, по этому мы вынуждены понимать его английские обозначения. О том, что калькулятор нас внимательно слушает, он сообщает надписью в окошке с открытой скобкой. Все свои действия калькулятор дублирует над окошком ввода данных, где ещё раз напоминает нам о том, что все числа он слушает на языке радиан - под тангенсом маленькая надпись "2 пи".

Тангенс пи с наворотами

Дальше просто нажимаем кнопочки цифр и математических действий: тридцать восемь умножаем на пи и делим на три. Нажимаем кнопочку "равно" и получаем результат. Закрывать скобку после набора всех цифр не обязательно - умный калькулятор сам догадается открытую скобку закрыть. Число "пи" также искать и вспоминать не нужно, для него есть специальная кнопочка "pi". Нажимаете эту кнопочку и калькулятор прекрасно понимает, о каком именно числовом значении вы говорите.

Тангенс пи с наворотами

Если вы измените порядок выполнения действий - тридцать восемь разделите на три а потом умножите на пи, то и в этом случае калькулятор поймет вас именно так, как надо.

Тангенс пи с наворотами

Всё, значение тангенса 38/3 пи мы нашли. Если же вы хотите быть такими же умными, как калькулятор, тогда нужно разобраться, что и как он делает. Проделаем это и мы.

Прежде всего, нужно убрать все навороты по 2 пи из значения угла. В нашем случае таких наворотов аж шесть или в дробном выражении 36/3. Возвращаем эти навороты туда, откуда их взяли математики - выбрасываем в мусор. У нас остается значение угла в 2/3 пи.

38/3 = 12,67 - это столько пи в нашем углу (многовато будет)

12,67/2 = 6,3 - это означает, что в нашем углу целых шесть наворотов

6*2 пи = 12 пи = 36/3 пи - это нужно выбросить из угла в мусорное ведро (стоит на кухне, но лучше уточнить по месту)

38/3 пи - 36/3 пи = 2/3 пи - это тот угол в радианах, с которым мы фактически имеем дело

Теперь нам нужно переварить эти самые 2/3 пи. Поскольку 2/3 пи больше, чем 1/2 пи, воспользуемся формулой приведения тангенса

2/3 пи = пи - 1/3 пи

tg (2/3 пи) = tg (пи - 1/3 пи) = -tg (1/3 пи)

По таблице значений тригонометрических функций находим, что тангенс 1/3 пи равняется корню квадратному из трех. Цепляем к этому значению знак "минус" и нужный нам ответ получен. Можете проверить на калькуляторе - извлеките квадратный корень из трех и дорисуйте знак "минус".

Естественно, при решении подобных примеров у меня не мог не возникнуть вопрос: есть ли сегодня на Земле хоть один человек, который в своей повседневной практике, без всякого принуждения со стороны математиков, использует для описания вращения градусы или радианы? Если такой человек всё же найдется, хочу у него спросить: ну как, удобно? Дело в том, что инженеры вращение научились измерять в оборотах. Без всяких 2 пи или 360 градусов. Мне кажется, математикам уже давно пора вылезать из своих склепов определений и посмотреть вокруг, как разумная жизнь решает задачи. Зачастую, гораздо проще и эффективнее, чем это делают наши математики.

Блондинка и инопланетяне

Автор Николай Хижняк

Не научные, но фантастические приключения блондинок с элементами реализма. Продолжение рассказа о первом законе физики и других законах.

Глаза блондинок расширились от удивления:

- У инопланетян тоже есть блондинки?!

- Нет, блондинок у инопланетян нету. Во всяком случае, в нашем понимании. Есть среди них существа, логика и образ мыслей которых несколько отличаются от стандартных.

- Психи, что ли? – брезгливо уточнила одна из блондинок.

- Ну… не совсем. Инопланетяне к ним относятся иначе, чем ко всем остальным. Между собой инопланетяне называют их «другие». Мне о них мало что известно. Я знаю только то, что «другие» очень часто являются своего рода генераторами нестандартных решений и что среди «других» у инопланетян живет одна земная блондинка…

Шок отразился на лицах блондинок:

- Как это? Что она там делает? Как она туда попала? Кто она такая?... – после некоторой паузы вопросы блондинок посыпались, как из рога изобилия.

- Так, спокойно. Об этой блондинке я знаю совсем чуть-чуть, - я начал вспоминать всё, что мне известно об этой блондинке от инопланетян, - Собственно говоря, благодаря существованию этой блондинки, я познакомился с инопланетянами… Да, теперь можно это точно сказать…

- Вас с инопланетянами познакомила блондинка!? А как вы познакомились с нею? – эти вопросы вырвались у блондинок сами собой.

- Нет, я никогда не встречался с этой блондинкой и о моем существовании она вряд ли догадывается, – продолжал я свои размышления вслух, – Инопланетяне сами связались со мной. Сперва они меня кое-чему научили… Кода инопланетяне поняли, что я кое-то уже начал понимать, они предложили мне решить одну задачу… В этой задаче речь как раз и шла о блондинке с нашей планеты…

- А что за задача? Вы ё решили? А почему обратились именно к вам? – на лицах блондинок читалось недоумение.

- О задаче мы с вами поговорим как-нибудь позже… Чтобы понять её смысл, вам нужно немножко больше знаний, - мой ответ слегка утихомирил возбуждение блондинок, - Нет, я задачу не решил. Мне кажется, что она из разряда тех, которые в принципе не могут иметь правильного решения. Эту задачу придумали сами инопланетяне… Точнее, они поняли, что эту задачу, скорее всего, им придется решать в будущем. Инопланетяне решили заранее найти правильное решение и не смогли. Даже их «другие» оказались бессильными. В подобных ситуациях инопланетяне часто обращаются к существам с тех планет, за жизнью на которых они наблюдают. У таких существ другой образ мышления, другой набор знаний, другая логика… Иногда инопланетянам удается получить решение, о котором они не подозревали. Вот меня и выбрали в качестве одного из таких существ – калькуляторов для решения чужой задачи, – я грустно улыбнулся, – Понятно, что перед использованием калькулятор нужно хоть чему-то обучить…

- Да уж, ситуация, – сочувственно произнесла одна из блондинок, – А нас вы тоже на калькуляторов для инопланетян готовите? – дерзко спросила вторая.

- Нет, с вами я занимаюсь по своей доброй воле. Тут такое дело, - я оценивающе взглянул на блондинок, определяя, стоит ли говорить им то, что я собирался сказать, - При общении со мною, инопланетяне называли нашу блондинку не иначе, как «Богиня»…

- Ничего себе, имечко. А поскромнее имена у них есть? – возмутилась одна из блондинок.

- Точнее, на инопланетном языке её назвали «Та, Которая Создает Вселенные». В нашем понимании это и будет «Богиня». Но… Созданием вселенной никого из инопланетян не удивишь. Даже их детишки в детском садике имеют представление о том, как создаются вселенные. Создание вселенной для инопланетян приблизительно то же самое, что для нас строительство нового города. Если это нужно сделать – они делают, если это не нужно – никто вселенные просто так не создает. Вот и возникает вопрос: что могла сделать блондинка такого, что произвело такое впечатление на инопланетян? Сами инопланетяне считают нашу блондинку «другой» и относятся к ней с большим уважением. Вполне возможно, что она относится к числу тех немногих, кто определяет пути дальнейшего развития цивилизаций инопланетян.

- Круто девочка устроилась, – вслух подумала одна из блондинок.

- Конечно, это всё мои догадки, – поспешно уточнил я, – прямым текстом мне говорили не так уже и много, но по отношению инопланетян к героине задачки кое какие выводы можно было сделать. Нужно будет попытаться у инопланетян побольше разузнать об этой блондинке.

- Я в шоке. Как такое может быть? – озадаченно спросила одна из блондинок. Информация о блондинке среди инопланетян произвела на них очень сильное впечатление.

- Наверное, эта блондинка умеет пользоваться своими мозгами, – высказал я свое предположение, – Думаю, и вы ничем не хуже её. Только для этого вам нужно знать чуточку больше, чем вы знаете сейчас. Прежде всего, нам нужно найти другую, пригодную для нас, планету.

- Прямо сейчас? – вяло уточнила одна из блондинок.

- Для «прямо сейчас» у нас нет ни знаний, ни денег, ни технологий… – начал, было, я.

- Печалька, – грустно добавила вторая блондинка.

Всё, продолжать дальше не имело смысла. Блондинки пребывали в полной апатии и мысленно находились где-то на далеких галактиках, среди инопланетян. Думаю, даже появление настоящего инопланетянина не способно было вернуть их к реальности.

Я проводил блондинок до двери, они вяло попрощались. Во избежание несчастных случаев на дороге, мне пришлось сопровождать их аж до самого дома.

Первый закон физики и другие законы

Автор Николай Хижняк

Не научные, но фантастические приключения блондинок с элементами реализма. Продолжение рассказа о детском садике инопланетян.

Вопрос застал блондинок врасплох. Они переглянулись, инстинктивно пошарили по туловищу в поисках шпаргалки, снова переглянулись и начали тихонько перешептываться. Одна из них спросила:

- А первый закон какого дядьки?

- Когда научный закон выходит замуж за ученого, он берет его фамилию. Если закон выходит замуж сразу за двух ученых, он носит двойную фамилию, – я улыбнулся.

Понятно, что от всего процесса обучения у блондинок в памяти остались лишь жалкие обрывки полученных знаний. Они помнят, что какие-то законы есть и что эти законы носят чьи-то фамилии. Задав вопрос, они надеялись, что фамилия ученого поможет им извлечь из памяти затерявшуюся формулировку.

- Я говорю не о законе «какого-то дядьки или тётки», я говорю о законе, который инопланетяне ставят перед всеми остальными законами. Наши ученые сформулировали бы этот первый закон физики так: «любые изменения количества любой физической величины выражаются математическими действиями сложения и вычитания». При этом инопланетяне считают самым важным не набор слов, а их смысл. Вспомните свое детство. Если мы к зайчикам прибавим зайчиков, зайчиков станет больше. Если отнимем – зайчиков станет меньше. При этом зайчики не могут превратиться ни в бабочек, ни в улиток, ни во что-то другое. Для превращения не достаточно просто прибавлять или вычитать, нужно сделать что-то другое. Вспомните нашу народную мудрость – сколько раз не повторяй слово «халва», во рту сладко не станет. Смысл этой мудрости точно такой же, как и у первого физического закона. Для инопланетян не имеет значения, какими словами вы сформулируете первый закон физики – зайчиками, халвой или физической величиной. Для них главное, что бы вы понимали смысл.

- Сколько волка не корми, он всё равно в лес смотрит, – сказала одна из блондинок, вторая удивленно на неё посмотрела.

- Да, и это тоже выражение первого закона физики. Заметьте, инопланетяне не разделяют весь окружающий мир на отдельные самостоятельные науки. В первом физическом законе физика и математика неразрывно связаны друг с другом. Инопланетяне рассматривают все науки как разные грани одного целого. Как нельзя разорвать окружающий мир на кусочки, так нельзя одну науку отделить от другой. «Разделяй и властвуй» - этот древний принцип рабовладельцев благополучно господствует в науке и в наше время. Все науки, по идее, должна объединять философия.

- Ой, а я слышала про философию! – радостно вставила одна из блондинок, – Там даже какие-то законы есть. Закон спиральки, кажется…

- Да, в философии говорят о каких-то общих законах. Но что это за законы? Их сформулировали посторонние наблюдатели, которые попытались описать то, что видят. Например, закон спирального развития – это не больше, чем закон граблей. Не наступайте на те самые грабли, на которые вы уже наступили, и грабли не будут снова бить вас по голове. Это закон развития разумных существ. Мы же живем по закону безмозглых созданий, не способных учиться на собственном опыте. Чем дольше наступаешь на грабли, тем больнее они бьют по голове - к такому выводу пришли наши философы. В этом и заключается смысл философского закона о спиральном развитии. История повторяет свой урок до тех пор, пока живые существа его не усвоят. Либо на уровне инстинктов, либо на уровне разума. Если мы не будем убивать друг друга, тогда исчезнет вся спиральность войн. Если мы не будем со всей дури тянуть экономическое одеяло на себя, тогда не будет экономических кризисов. Кстати, в основе всех экономических кризисов лежат самые примитивные свойства отрицательных чисел. Не те свойства, о которых нам рассказывают математики, а те, о которых они, похоже, и сами ничего не знают.

- Разве могут математики что-то не знать о свойствах чисел? – удивленно спросила блондинка.

- Конечно, могут. Невозможно знать всё обо всём. Даже инопланетяне многих вещей не знают. Но они научились безболезненно выбрасывать старые знания и заменять их новыми. Нам же до этого ещё очень далеко. Например, возьмем философский закон о переходе количества в качество. Сколько метров длины нужно взять, чтобы получилась площадь? Сколько ниток нужно отмотать с катушки, чтобы получилась ткань для одежды. Для получения площади длину нужно не складывать, а умножать. Для получения ткани нитки нужно не просто отматывать, но и переплетать между собой. Но любой философ скажет вам, что вы рассуждаете не правильно. Если взять три длины, то по формуле Герона вы можете получить площадь. Если нитки обматывать вокруг себя, то получится одежда, как кокон у шелкопряда. Чтобы вы не говорили философам, правы всегда будут они, а не вы. По сути своей, философия является не наукой, а искусством делать дураков из окружающих. Основана философия на вере в справедливость сформулированных философами законов. А там, где начинается вера, там заканчивается здравый смысл. Какие бы доводы, опровергающие законы философии, вы не приводили, философы всегда будут утверждать, что вы ничего не понимаете в их законах. Математика основана на вере в определения. Таким образом, и философия, и математика ничем не отличаются от религии. Проповедники этих «наук» просто передают нам свои знания и учат, где и как ими нужно пользоваться.

- Не поняла… А как же развитие техники? Как могла развиваться наша техника, если науки не правильные? – удивленно спросила блондинка.

- Нужно на нашу историю смотреть со стороны и видеть её целиком, а не просто изучать отдельные даты и события. Философия к технике не имеет никакого отношения – это чистые проповедники своих (или чужих) взглядов. Религия – это философия верующих, философия – это религия атеистов. Поставьте знак равенства между философией и религией и попытайтесь найти отличия. Да, некоторые различия есть, но по сути – это одно и то же. Слепая вера в правдивость слов, сказанных когда-то кем-то из людей. Вы всегда говорите правду окружающим? В том то и дело, что ради себя, любимого, можно и соврать. Лично я уже не верю чужим словам, кто бы их не говорил. Я верю только в результат. И вам советую. Инженеры, создающие технику, с математиками поступают точно так же – они используют только результаты их расчетов и не обращают никакого внимания на то, что при этом математики говорят и делают. Так в древности охотники и земледельцы использовали шаманов. Никто не понимал того, что делают шаманы во время своих обрядов, все ждали тех слов, которые шаманы скажут в конце своего ритуала. Для наших инженеров математики являются не больше, чем калькуляторами. При этом не нужно забывать, что инженеры и математики принадлежат к разным бюрократическим системам. Инженеры не вмешиваются в бюрократическую систему математиков. По умолчанию, между разными бюрократическими системами всегда действует принцип невмешательства. Сами же бюрократические системы существуют по одному общему закону: уровень маразма любой бюрократической системы определяется уровнем маразма её руководителей. Каждая бюрократическая система стремится к состоянию покоя и старается избавляться от тех, кто этот покой нарушает. Вот почему все наши вундеркинды превращаются в рядовые винтики бюрократической системы. Вся система образования направлена на подготовку послушных исполнителей воли вышестоящих руководителей…

- Это вам инопланетяне про нас такое рассказали? – блондинки встревожено смотрели на меня, как смотрят на душевно больного, потерявшего контроль над собой.

- Нет, инопланетяне мне этого не говорили. Это я сам пришел к таким выводам. Кстати, при анализе я использовал любимые нашими математиками обобщения и расширения. Не волнуйтесь, всего, что я вам сейчас наговорил, учить и запоминать не нужно. Хотите – пользуйтесь моими знаниями, не хотите – не пользуйтесь, дело хозяйское. Это мои обобщения некоторых принципов нашего исторического развития. Зная их, гораздо проще понять, почему у нас всё происходит именно так, а не иначе…

- А инопланетяне изучают нашу историю? – уже с некоторым интересом спросила одна из блондинок.

- Нет. Зачем инопланетянам нужна наша история? Одного беглого взгляда на нашу цивилизацию достаточно, чтобы понимать, с кем имеешь дело и чего от нас можно ожидать.

- И кем же инопланетяне нас считают? Почему они не вступают с нами в контакт? – с явным интересом спросила блондинка.

- Давайте об этом поговорим как-нибудь в другой раз. А сейчас вернемся к первому закону физики, – я попробовал перевести разговор на первоначальную тему.

- А истории про факториал и про гостиницу вы откуда знаете? – не унимались блондинки.

- Эти истории я сам придумал специально для вас. Чтобы вам было интересно…

- А та блондинка в истории про бесконечную гостиницу – это мы? – уточнила одна из блондинок.

Здесь мне пришлось задуматься над ответом. Можно просто соврать и избежать лишних вопросов. Можно сказать правду, но тогда придется отвечать на те вопросы, ответов на которые я не знал и над которыми особо не задумывался.

- Нет, это не вы. Это совсем другая блондинка, о которой я почти ничего не знаю. Эта блондинка живет среди инопланетян, – честно ответил я.

Прямоугольный параллелепипед

Вновь поступил вопрос про прямоугольный параллелепипед. И вопрос этот не простой, смотрите сами:

Рёбра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите площадь его поверхности. Подскажите, как это переварить?

Прямоугольный параллелепипед площадь поверхности

Вопрос, конечно, не простой - что такое прямоугольный параллелепипед, как и с чем его едят? В частности, как найти рецепт приготовления площади поверхности этого то ли фрукта, то ли овоща? Так, для начала давайте посмотрим, что это вообще такое - прямоугольный параллелепипед? Вот картинка прямоугольного параллелепипеда.

Прямоугольный параллелепипед

Как видите, прямоугольный параллелепипед - это, собственно, обыкновенный кирпич. Кстати, если бы Ньютону на голову упала не сфера в виде яблока, а прямоугольный параллелепипед в виде кирпича, то в школе мы вряд ли бы учили его законы. Прямоугольная комната - это тоже прямоугольный параллелепипед, который позволяет вам совершить обзорную экскурсию по его достопримечательностям прямо изнутри. Если вы хотите произвести внешний осмотр достопримечательностей сего математического чуда, тогда возьмите в руки коробку из-под обуви и можете вертеть её, сколько душе угодно.

И так, прямоугольный параллелепипед на картинке дает нам возможность увидеть вершины, ребра и диагонали. Вершины мы можем потрогать пальцем, ребра мы можем измерять, диагональ можем высчитать. Нам сейчас диагональ не нужна. Закон движения учеников в классе знаете? Если леди-учитель покидает класс, класс движется быстрее. Закон решения задач очень похож: чем меньше всякой ерунды нам нужно искать, тем проще задача.

Первая проблема, с которой мы сталкиваемся в задаче, это проблема сленга. Задача сформулирована на бытовом сленге, а все формулы и определения в математике формулируются на математическом сленге. Поэтому нам самим предстоит выполнить перевод. Приступаем к поэтапному переводу, по фразам.

"Рёбра прямоугольного параллелепипеда, выходящие из одной вершины ..." - собственно, здесь говорится о тех ребрах, которые позволяют нам определить размеры прямоугольного параллелепипеда и на основании этих размеров выполнить все необходимые вычисления. На картинке это ребра a, b и c. Кто бы сомневался, что именно эти три ребра нам дадут по условию, но только не я. Ни один математик вам этого не скажет (не потому, что они этого не знают, а из боязни нарваться на очень неудобные вопросы), но если в условии задачи дать две длины параллельных ребер и одного перпендикулярного им, то нашу задачу в принципе решить будет невозможно. В прямоугольном параллелепипеде из любой вершины всегда выходит три взаимно перпендикулярных ребра. Вот по этому в нашей задаче прямо говорится об этом. Если верить Священным Писаниям разных религий, то именно из одного такого ребра сотворены все прямоугольные параллелепипеды, задачи о которых решает вся прекрасная половина человечества.

Следующая фраза "... равны 1, 2, 3" обозначает, что нам не нужно искать этот злополучный прямоугольный параллелепипед и свою линейку, чтобы измерить длины его граней, как это показано на рисунке. Тот, кто эту задачу придумал, уже сам всё измерил (или выдумал эти размеры, что в данном случае принципиального значения не имеет). Кто есть кто в этом списке чисел? Где длина, ширина, высота нашего параллелепипеда? Нам это без разницы. Как бы мы этот прямоугольный параллелепипед не крутили, площадь его поверхности всегда будет оставаться неизменной. Предыдущие поколения математиков этот факт не единожды проверили. Когда мы доберемся до решения, мы сами в этом убедимся.

Теперь вопрос, в чём же конкретно измеряется наш прямоугольный параллелепипед и площадь его поверхности? В каких единицах измерения? Ответ довольно прост - в любых единицах измерения длины. Англичане и американцы любят дюймы, футы, мили. Мы предпочитаем сантиметры, метры, километры. В чем измеряют длину инопланетяне? Мы вообще не знаем. Да нам эти единицы измерения и не важны. В чем бы мы не измеряли длину граней, циферки возле длин и площади будут одинаковыми. Циферки остаются, единицы измерения меняются. Вот два способа получения результата в математике.

разные числа + одинаковые единицы измерения = разный результат

одинаковые числа + разные единицы измерения = разный результат

Приблизительно, как в этом счетчике. Крутим одно колесико - меняются числа. Крутим другое колесико - меняются единицы измерения. Так устроена настоящая математика, маленький кусочек которой мы сейчас рассматриваем.

Математика

Это уже не детская математика, придуманная специально для того, чтобы мучить нас задачками. Это взрослая математика, одинаковая для всех.

В нашей задаче мы измеряем всё в абстрактных единицах измерения длины. Соответственно, полученная нами площадь будет измеряться в этих же единицах измерения, возведенных в квадрат.

Теперь нам осталось только достать из глубокого кармана шпаргалку с формулами для прямоугольного параллелепипеда и посмотреть, чего полезного для нас там имеется.

Прямоугольный параллелепипед формулы

Что вообще есть в этой шпаргалке? Формула диагонали прямоугольного параллелепипеда, формула объема. Есть несколько формул для площади поверхности: полная, основания, боковая. Вот одна из этих формул нам как раз нужна. Разберемся в площадях на примере коробки для обуви. Площадь основания - это площадь донышка или крышки коробки. Площадь боковой поверхности - это боковые стеночки коробки без донышка и крышки. Полная площадь - это боковые стеночки вместе с донышком и крышкой.

Теперь смотрим в условие задачи и определяем, "чё тебе надобно, старче?". А надобно ему (ей, им) "площадь поверхности". Если уточнений типа "боковой" или "основания" нет, значит искать нужно полную площадь поверхности прямоугольного параллелепипеда. Длины трех граней у нас есть, формула тоже, можно произвести расчет. Заморачиваться с основаниями и боками нам нет смысла.

Прямоугольный параллелепипед решение задачи

Как видим, полная площадь поверхности нашего прямоугольного параллелепипеда получилась равной 22 единицы в квадрате. Какие именно единицы? А какие вам не жалко или какие вы больше всего любите.

По просьбе учащихся добавляю картинку про сумму длин ребер прямоугольного параллелепипеда.

Прямоугольный параллелепипед периметр

Сумму длин всех ребер параллелепипеда я обозначил через букву "P", поскольку она очень похожа на периметр прямоугольника. Кстати, в формуле длин всех ребер я этого не записал, но если мы возьмем три фигурообразующие грани прямоугольного параллелепипеда, которыми являются прямоугольники, то сумма длин всех ребер параллелепипеда будет равна сумме периметров этих прямоугольников.

Математические принципы инверсии и выворачивания

Не научные, но фантастические приключения блондинок с элементами реализма. Завершение отдельной истории.

Прежде всего, мы изучили определение инверсии. Дебри этого определения оказались для блондинок непролазными. Специально для блондинок я подчеркнул те моменты, которые считал наиболее важными.

Инверсия определение

Инверсия пример

- Так, давайте не будем вдаваться в анатомические подробности этого священного для математиков текста. Просто отметим, что по сути своей инверсия является выворачиванием пространства относительно окружности. При этом математики выкалывают центр этой окружности. Почему? Очевидно, математикам жалко выкалывать себе глаза, поэтому они выкалывают центр окружности, чтобы не видеть всего того ужаса, который происходит при инверсии этого центра. И ещё. Математики считают, что инверсии подвержены пространства с любым количеством измерений, в том числе и трехмерное пространство, в котором мы обитаем. Так почему инверсия не срабатывает при выворачивании мешка?

Блондинки активно занялись поиском ответа на этот животрепещущий вопрос. Они вертели в руках мешок, гладили пальцем окружность отверстия, заглядывали внутрь…

- Мне кажется, - многозначительно заявила одна из блондинок, - всё дело в центре окружности. Если его найти и выколоть, тогда у нас всё получится – мы вывернем пространство наизнанку. Булавка у меня есть.

Да, у нас было всё – и пространство, и окружность, и булавка для выкалывания центра, вот только сам центр куда-то пропал. Смешно тыкать булавкой в пустоту.

- Так, я думаю, что это бракованный мешок. Производитель не сделал в нем центр окружности, вот мы и не можем его найти. Может, мешок просветить рентгеном? – сказала одна из блондинок.

- Нет, этот центр окружности просто ещё не родился. Нужно ему УЗИ сделать, – в тон ей ответила другая блондинка.

- Типичная проблема экспериментальной физики – физики не могут найти то, что так ясно видят математики. Давайте не будем играть в обезьяну и очки, а попробуем найти решение в самой математике. На каких математических принципах построена математическая инверсия? – мой вопрос заставил блондинок переглянуться.

- В Википедии такого не написано, а знакомого математика я с собою в косметичке не ношу. Он умный и всё знает, - оправдалась одна за двоих.

- Думаю, такого и он не знает, - начал я свое пояснение, - Его этому вряд ли учили. Хотя, сама задача решается довольно просто. Нужно всего-навсего проанализировать то, что записано в формуле определения инверсии. Видите, там радиус окружности указан? Есть ещё два расстояния от точек до центра окружности, которые с радиусом окружности никак не связаны. Все эти расстояния измеряются в единицах измерения длины, которые на свойства инверсии никак не влияют. Присутствие радиуса в формуле свидетельствует о том, что данная форма записи не является чисто математической. Это прикладная форма, которой мы пользуемся при решении задач. Точно такой же прикладной формой основного тригонометрического тождества является теорема Пифагора. Для перехода к математической форме инверсии нам нужно избавиться от радиуса окружности. Расстояние от центра инверсии до точек не зависят от радиуса окружности, их можно оставить неизменными. Для того, чтобы избавиться от радиуса окружности, нам просто достаточно принять этот радиус за единицу измерения расстояний при инверсии. Смотрите, что при этом получается.

Блондинки с интересом наблюдали за моими манипуляциями с радиусом.

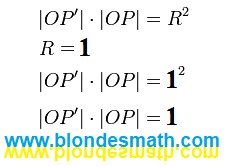Математические принципы инверсии

- Теперь мы можем легко выразить одно расстояние до точки через другое.

Математические принципы инверсии

- Как видите, в основу инверсии, как её понимают математики, положена обратная симметрия. В основе такого принципа обмена лежит психология нищих жадных обезьян: «Меняю всё, что есть у меня, на всё, что есть у вас, у всех, вместе взятых». Инверсия нулевой точки будет отражением психологии мародеров: «Я – пуп земли и всё принадлежит мне!».

- А разве может математика рождаться из нашей психики? – удивление было написано на лице блондинки.

- В этом мире всё взаимосвязано. О любой цивилизации можно очень много узнать, посмотрев какая математика у них есть и как именно эта цивилизация нею пользуется. Если вы когда-нибудь станете специалистами по внеземным цивилизациям, с математики будете начинать…

- Эт чё, инопланетяне считают нас тупыми жадными мародерами? – задумчиво спросила одна из блондинок. Хорошее настроение блондинок сразу куда-то улетучилось. Я попытался спасти ситуацию:

- Ну, во-первых, мы рассматриваем только инверсию. Нельзя делать поспешные выводы на таком малом количестве данных. Во-вторых, мы все разные…

- А в-третьих? – грустно спросила блондинка.

- В-третьих, если бы инопланетяне считали вас тупыми жадными мародерками, они не пустили бы вас на свою летающую тарелку. Вы у них хоть что-то украли себе на память? – блондинки отрицательно покачали головами, – Вам инопланетяне показали самые красивые виды на разные уголки космического пространства, которые были у нас на пути…

Ложь во имя спасения. Наверняка, блондинки считали, что я уже много раз путешествовал на летающих тарелках и повидал всякого. Они думают, что в тот раз инопланетяне специально для них показали то, что мне уже давно примелькалось. На самом же деле, я в тот раз летел впервые, как и они. Кому из нас показывались все эти космические пейзажи? Безымянная спиральная галактика, закрывающая половину небосвода… Газопылевое облако невероятных оттенков… Черная дыра у границы сингулярности не понятно с какой стороны… Блондинки были настолько потрясены этой красотой, что моего восхищения они не заметили. Кому именно всё это было показано – мне или им? Разве это так важно? Мы это видели, все вместе, и этого вполне достаточно.

- … И заметьте, в три часа ночи не меня они высадили возле моего дома, а вас – у вашего, мне же пришлось до утра у вас ютиться.

Последний аргумент возымел действие, блондинки слегка приободрились:

- И что всё это значит? – с нескрываемой надеждой спросила одна из них.

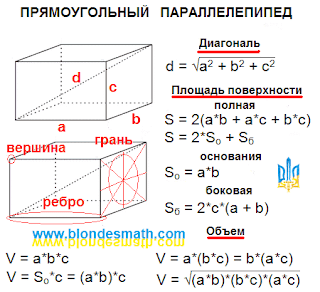
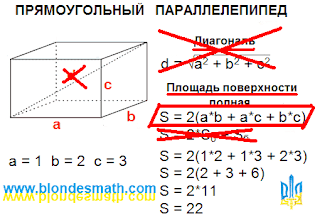
- Ровным счетом ни-че-го, не надейтесь, – при этих словах я улыбнулся, что только усилило тайные надежды блондинок, – Инопланетяне просто показали, что они могут быть очень вежливыми и о наших правилах хорошего тона кое-что знают. Вот такие джентльмены с далеких галактик. Но давайте вернемся к нашей инверсии. В Википедии, с присущей нам гордостью, указывается аж два случая применения геометрической инверсии. На это посмешище я даже смотреть не стал. Реально инверсию можно представить как отражение окружающего мира в зеркальном шаре. А вот выворачивание, в отличие от инверсии, нужно строить на простой симметрии. При выворачивании должно соблюдаться равенство площадей или объемов, если мы выворачиваем мешок. Сколько вывернули наружу, столько же получили во внутрь. В этом случае окружность будет являться осью симметрии, а точка «ноль» всегда будет располагаться на окружности. В центре окружности будет точка «единица», выкалывать которую я не вижу причин.

- А разве точка ноль может быть в виде окружности? – изумленно спросила одна из блондинок.

- Конечно, может. А что здесь странного? В инверсии мы имеем нулевую точку в центре и точку «единица» в виде окружности. При выворачивании круга они меняются местами: «единица» – это точка в центре, «ноль» – это окружность. Вас же не смущает то, что в осевой симметрии точка «ноль», она же ось симметрии, имеет вид прямой линии? Правда, математики как-то не очень любят афишировать этот факт. Впрочем, я не настаиваю на своем утверждении – понятия «точка ноль» и «точка единица» являются относительными, об этом мы с вами поговорим как-нибудь в другой раз. А сейчас давайте посмотрим на выворачивание в тех же обозначениях, которые били в инверсии.

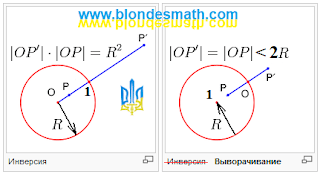Математические принципы инверсии и выворачивания

- В качестве оси симметрии при выворачивании можно брать замкнутую линию любой формы. Правила выворачивания тоже можно сочинять самим. Я не знаю, есть ли в математике что-то подобное. Тратить весь остаток своей жизни на тщательное изучение всех разделов математики в поисках инверсии, основанной не на обратной, а на обычной симметрии – я считаю это глупостью. Кому сильно нужно разработать математическую модель выворачивания мусорного мешка, пусть занимается. Мы просто посмотрим на пару вариантов выворачивания прямоугольника.

Математические принципы инверсии и выворачивания

- Можно разрезать пространство внутри прямоугольника какими-то линиями, вывернуть по линиям разреза, можно вывернуть всё внутреннее пространство прямоугольника относительно одной из сторон… Вариантов масса. При разрезании внутреннего пространства, естественно, возникает вопрос: куда попадут точки, лежащие на линии разреза? Здесь нужно применять математическую теорию вероятностей. Для первого рисунка центральная точка после выворачивания может оказаться в одной из возможных четырех точек. Точки, лежащие на линии разреза, могут занимать одно из двух возможных положений. Естественно, создателей оружия такая математика устраивать не может – им нужно точно знать, куда полетит пуля после выстрела. А мне безразлично – я из выворачивания стрелять не собираюсь, и вам не советую.

Блондинки захихикали, одна спросила:

- А причем здесь создатели оружия?

- Ну как причем? Обычно основное финансирование науки осуществляется ради создания новых видов оружия. Вот стрелкИ и выкручивают руки ученым, в том числе и математикам, требуя точных результатов. Второй вариант выворачивания им подойдет гораздо больше – он очень похож на осевую симметрию, когда ось симметрии совпадает с одной из сторон прямоугольника. В этом случае все точки ложатся точно в цель. Но оставим военные игры взрослым детишкам, для нас гораздо важнее многомерные варианты инверсии. Выворачивание также можно производить в пространствах с разным количеством измерений. А вот этот принцип, в отличие от инверсии, можно положить в основу телепортации – один трехмерный объем меняется на равный ему другой объем. Разрезать и выворачивать при этом ничего не нужно, достаточно просто произвести симметричный обмен. Когда начнете разрабатывать математические принципы телепортации, советую вспомнить то, о чем я вам сейчас рассказал. Очень может пригодиться.

- А нам обязательно нужно будет заниматься этой самой... Как её? Теле... Теле... Телепортацией! - спросила одна из блондинок.

- Надеюсь, вы не собираетесь сидеть до скончания века на этой планете в ожидании того, что кто-то обделает вас своим счастьем? Как уверяют ученые, 65 миллионов лет назад один счастливый метеорит встретился с нашей планетой. По случаю этого знаменательного события он устроил грандиозный фейерверк. Думаю, с поверхности Марса это действительно выглядело красиво. Только вот динозавры, обитавшие как раз в то время на нашей планете, не смогли пережить чужое счастье - они все вымерли. Вы хотите повторить их подвиг?

На этом я закончил свою презентацию пылесоса и попрощался с блондинками до следующей встречи.

Инверсия в математике и мешки к пылесосу

Автор Николай Хижняк

Не научные, но фантастические приключения блондинок с элементами реализма. Просто отдельная история.

Две запыхавшиеся блондинки стояли перед моей дверью, по их виду можно было сказать, что летели они ко мне, как на пожар. Я отступил в сторону со словами:

- Заходите, вы мне очень срочно нужны.

- Что случилось? – в голосе одной из блондинок звучала неподдельная тревога.

- Я получил письмо счастья и мне срочно нужно ним с кем-то поделиться.

Глаза блондинок округлились, личика их презрительно скривились, непонимающе переглянусь, одна спросила:

- Вы верите в эту ерунду?!

- Ну, во-первых, я не верю в то, что какая-то там девочка десять раз переписала письмо, и на неё тут же с неба ляпнуло счастье. И вот теперь эта девочка вся обделанная счастьем, а мы – нет, потому что письмо не переписали. Кстати, вот почему коровам запрещено летать – чтобы на нас с неба их счастье не свалилось. Во-вторых, мое счастье имеет вполне конкретное денежное выражение, хотя принцип его получения очень похож на распространение письма счастья.

Блондинки разочарованно топтались в дверях, но в их глазах засветились искорки любопытства.

- Проходите, сейчас я вам всё объясню, - мы прошли в комнату, - Мне нужно провести презентацию пылесоса, за это мне заплатят копеечку. Презентацию нужно провести среди множества потенциальных потребителей этого замечательного товара. С точки зрения математики, даже одна из вас уже является математическим множеством, состоящим из одного элемента. Но с точки зрения рекламодателя, это математическое множество множеством потребителей не является. Вот поэтому я пригласил вас двоих. Теперь рекламодатель не сможет заявить, что два человека – это не множество.

Уловив смысл сказанного, и зная меня, блондинки поняли, что сейчас их ожидает урок математики. На их лицах отразился неподдельный интерес. Чем всё это кончится? Куда в математику можно засунуть пылесос, пусть даже это самый крутой пылесос в мире?

- Для проведения презентации мне дали во временное пользование это чудо техники. Отчет о проделанной работе я должен предоставить в виде видеорока, так что красьте губки, наводите марафет – нас будет снимать скрытая камера!

- Нас покажут по Ютубу? – с надеждой спросила одна из блондинок.

- Лично я сильно сомневаюсь, что мой видеошедевр со столь многочисленными зрителями рекламодатель осмелится выложить на Ютуб, хотя … в этом мире возможно всё. А по сему, ваша красота должна затмить красоту какого-то там пылесоса, - улыбнулся я.

Как и положено на презентациях, я достал пылесос, текст презентации и приступил к исполнению своих обязанностей презентатора. Моя дурацкая привычка всё переводить на язык математики не заставила себя долго ждать:

- «… это дает возможность использовать пылесос …», - на этих словах я запнулся и дальше меня понесло, - Какая разница, в каком городе использовать пылесос? С тоски зрения не только математики, но и техники, все пылесосы одинаковы. С точки зрения географии одинаковы все города. Девочки, вы помните, как выглядят города на карте? Просто кружочки, которые отличаются только своим расположением на этой самой карте и буковками возле кружочков. Если сложить это вместе, то что пылесос Кирби в Ростове, что пылесос в Сан-Франциско будут совершенно одинаковы. Это только афроамериканцу, всё ещё проживающему в Африке, нужно смотреть по карте, где ему ближе покупать пылесос – в Ростове или в Сан-Франциско. Составлять график движения, преобразовывать этот график в математическую функцию, накладывать полученную функцию на систему координат нашей планеты, находить решение этой функции в сферической системе координат для двух конкретных точек… И всё это только для того, чтобы, в итоге, босыми ногами топтать африканскую пыль, которая ни в один пылесос не влезет…

Столь радужная перспектива практического применения математических знаний повергла в замешательство даже меня.

- Что ни говори, а математику нужно не только знать, но и уметь нею пользоваться… Ладно, мои ярко выраженные евроамериканки, проживающие за пределами Америки, продолжим нашу презентацию. Впереди нас ждет самое интересное.

Самое интересное началось тогда, когда мы перешли к замене мешков в пылесосе.

- Как человек экономный, я придумал одну маленькую хитрость. А что, если новые мешки не покупать, а просто стирать старые и использовать повторно? Ну, чисто теоретически. Вывернуть мешок наизнанку, вытряхнуть с него пыль, выстирать и снова вывернуть. Потом чистый мешок снова прикрепить к пылесосу. Кстати, выворачивание наизнанку очень похоже на математическую инверсию…

Одна из блондинок сняла мешок, ловко вывернула его наизнанку.

- Ты что делаешь? – возмутился я, - А если бы там была пыль?

- Я бы выполнила инверсию мешка над мусорным пакетом, – тут же ответила мне блондинка.

- Красиво звучит: «инверсия мешка над мусорным пакетом», почти как «мультипликативная операция над полем вещественных чисел», - задумчиво произнес я, - Заметьте, насколько умнее мы выглядим в глазах окружающих, когда произносим «умные» слова, обозначающие самые простые действия. Кстати, ты нас чуть не убила, если верить математикам. Инверсируй мешок обратно. Так, на всякий случай. Вдруг математики действительно правы?

Блондинка, теперь уже осторожно (видимо, чтобы не разбудить спящую математику), вывернула мешок обратно. Я продолжил свою мысль:

- Эта презентация и мешки к пылесосу предоставляют нам возможность повнимательнее присмотреться к такому математическому понятию, как инверсия. Почему при выворачивании мешка не происходит то, что должно происходить при математической инверсии? Ведь все признаки инверсии у нас имеются: отверстие в виде окружности, пространство внутри мешка и снаружи мешка. При инверсии мы с вами должны были оказаться внутри мешка, а собранная пыль – снаружи. Мы выворачиваем мешок – и вся Вселенная оказывается внутри мешка, пыль же распределяется по объему всей Вселенной. Именно так утверждают законы геометрической инверсии, которым нас учат математики. Почему эти законы не работают? Наш научный эксперимент с мешком полностью опровергает математическую теорию инверсии пространства. Давайте откроем Википедию и попробуем найти причину этого несовпадения теории с практикой.

Дальше мы погрузились в поиск различий между математическими принципами инверсии и выворачивания.