Математика в Википедии

Хотел стырить материал из Википедии и написать что-то полезное. Но математика в Википедии меня просто добила. После посещения отдельных математических страниц Википедии так и хочется сказать: "Никогда не делайте так, как делают математики!".

Я сам противник тупых догм, но всему есть предел. То, что делают математики - это дикая смесь полной анархии и религиозного догматизма. О том, что иллюстрации в Википедии часто не соответствуют тексту, я уже писал. Но и формулы записаны так, как будто их тупо повырезали из разных Священных Учебников Математики и вставили в одну статью. Остается только номера цитат прописать, как это принято при цитировании Библии. Вот пример фрагмента статьи о четырехугольниках.

Математика в Википедии

В соседних формулах диагонали и углы обозначены как кому понравилось. Я понимаю, что смысл от обозначения не зависит. Но менять обозначения по ходу повествования... Представьте, что великий русский поэт Пушкин в своем произведении "Евгений Онегин" в разных местах повествования называет своего героя разными именами: Евгений, Сергей, Вася, Ванька... Ведь главному герою литературного произведения автор может присваивать любые имена. Затем наш лихой парень превращается в застенчивую девицу, так же называемую по-разному. Это мы расшили понятие "главный герой литературного произведения" на женщин. Кто сказал, что женщины не могут быть героинями романов?

Интересно, много ли вы поймете, читая подобное литературное произведение? Может быть, по этому мы ничего не понимаем в математике, а только тупо зубрим определения? "Призма является разновидностью цилиндра"... А что, цилиндр не может являться разновидностью призмы?! Или от изменения иерархии у геометрических фигур поменяются математические свойства? Тогда давайте писать, как это принято в Библии: "Цилиндр родил Призму, Призма родила Параллелепипед, Параллелепипед родил Куб..." Все они выполняли заветы Математики, свято верили в Определения и после смерти попали в Комплексное Пространство...

Не знаю, как кого, а меня от такой пещерной математики в дрожь бросает. С кольцами математических действий в носу, с комплексными числами в руках вместо бубнов, современные шаманы выплясывают по кафедрам математики и проповедуют нам свои Определения. Аминь! ...Или "Равно!"? Нет, "Тож-дест-вен-но"... Наша современная математика тождественна религии. С математическими определениями сверяется результат. В науке же всё должно быть с точностью до наоборот.

Объем шестиугольной призмы

Как вычислить объем шестиугольной призмы? Объем всех призм вычисляется одинаково - площадь основания умножается на высоту призмы. Если основанием призмы является правильный шестиугольник, тогда у нас получается шестиугольная призма. Ещё такую штуку можно обозвать правильной шестигранной призмой. Она не обидится.

Быть правильным - в геометрии это круто! Обычно, неправильные геометрические фигуры, как зубная боль, донимают школьников. Их нужно делить на правильные фигуры, потом что-то там высчитывать... Хотя и с правильными геометрическими фигурами хлопот не меньше. Сведения о них нужно учить, потом вспоминать выученное... А оно очень быстро забывается.

Давайте посмотрим картинку с шестиугольной призмой и запишем формулу объема этой симпатичной фигурки.

Объем шестиугольной призмы

Как видите, для получения объема мы высоту призмы умножаем на площадь её основания. Основание нашей призмы - это правильный шестиугольник, площадь которого равна квадрату длины стороны, умноженному на три корня из трех и вся эта красота делится по братски, пополам. Собрав в кучку обе формулы, мы получаем формулу для нахождения объема шестиугольной призмы через длину стороны основания и высоту. От угла наклона граней призмы объем не зависит.

Не знаю, как математики могли пройти мимо такого удивительного факта - результат не зависит от угла наклона. Лично меня это шокировало. Я долго ломал голову в поисках ответа на вопрос: что всё это значит? Разгадка оказалась довольно простой - нужно знать место, где можно применить это удивительное математическое свойство геометрических фигур. Результаты, мягко говоря, поражают. Скоро мы это рассмотрим в "Приключениях блондинок".

Теперь решим задачу про объем шестиугольной призмы.

Основанием шестиугольной призмы служит правильный шестиугольник со стороной, равной а. Высота призмы равна h. Найдите объём этой призмы и вычислите его с точностью до 0,5 дм кубических, если а = 25 см и h = 40 см.

Сначала сделаем маленький анализ условия задачи. Сторона и высота шестиугольной призмы нам даются в сантиметрах. А вот объем от нас хотят услышать в кубических дециметрах, причем с точностью до 0,5. Злые демоны от математики снова хотят нас запутать. Чтобы не запутаться в переводе кубических сантиметров в кубические дециметры, я предлагаю поступить гораздо проще - перевести размеры из сантиметров в дециметры. Тогда объем мы получим сразу в кубических дециметрах.

а = 25 см = 2,5 дм

h = 40 см = 4 дм

Теперь мы можем подставить значения длины стороны основания и высоты шестиугольной призмы в формулу и вычислить объем. На калькуляторе это выглядит так.

Объем шестиугольной призмы

Мы получили шестьдесят четыре целых со здоровенным хвостом в 0,95190... и так далее. Теперь нам нужно это чудо округлить с точностью до 0,5. Это означает, что после запятой у нас должен стоять либо нолик, либо пятерка. Поскольку наш хвост гораздо ближе к единице, чем к половинке, то мы округлим его до целой единицы и прибавим её к уже имеющимся шестидесяти четырем единицам. В результате мы получаем ответ: объем шестиугольной призмы равен 65 кубических дециметров.

Измерения прямоугольного параллелепипеда

В комментариях к статье об объеме прямоугольного параллелепипеда появилась задача про измерения прямоугольного параллелепипеда. Измерениями параллелепипеда являются его длина, ширина и высота. Вот их и предлагается найти.

Найдите измерения прямоугольного параллелепипеда, если площади трёх граней соответственно равны 30, 48, 40 квадратных см

Не нужно перерывать все сведения о параллелепипеде в поисках решения этой задачи. Ни к геометрии, ни к параллелепипеду данное решение отношения не имеет. Смотреть нужно алгебру, решение системы трех каких-то там уравнений с тремя неизвестными. При чем же здесь параллелепипед? Это так математики хотели привязать решение систем уравнений к реальности. И, как обычно, промахнулись.

Для детских игр в числа условие задачи сойдет. А вот для взрослой математики такое условие не катит. Сразу же возникает совсем не детский вопрос: как можно было определить площади граней параллелепипеда, не зная его измерений? Ведь линейки у нас есть только для определения длины, ширины, высоты, расстояния, размера и так далее. Линейку для измерения площадей до сих пор никто не придумал. И, как я подозреваю, придумать её невозможно. Таковы математические свойства площадей. Площадь мы можем только вычислить, зная размеры геометрической фигуры. Но это так, лирическое отступление о качестве той математики, которой нас обучают. Вернемся к решению задачи.

Площадь грани параллелепипеда равна произведению одного измерения на другое. У прямоугольного параллелепипеда всегда три измерения. Комбинации умножения двух измерений из трех дают нам площади трех разных граней. Фактически, по условию задачи, нам дана система трех уравнений с тремя неизвестными. Обозначим измерения прямоугольного параллелепипеда через x, y и z. Запишем нашу систему уравнений и решим её методом подстановки.

Измерения прямоугольного параллелепипеда

Из третьего уравнения выражаем z через x. Подставляем полученное значение z во второе уравнение. Это нам дает возможность выразить y через x и подставить это значение в первое уравнение. В итоге этих не хитрых манипуляций у нас получилось одно уравнение с одним неизвестным. Задачка для детского садика. Вот только икс у нас получился в квадрате. Выковыриваем квадратный корень из числа и получаем значение икса. Отрицательное значение можем смело отбрасывать, поскольку отрицательных измерений размеров математики ещё не придумали.

Кстати, любой садист от математики может придумать отрицательную длину и получить за это очередную ученую степень. Ведь это только физики должны подтверждать свои идеи результатами экспериментов. Математикам достаточно придумать определение. И будем мы тогда изучать отрицательную длину так же, как сегодня изучаем комплексные числа.

По полученному значению x мы легко можем найти значения y и z. В результате у нас получилось, что прямоугольный параллелепипед имеет размеры 5, 6 и 8 сантиметров. Перемножая эти числа, вы легко получите площади граней прямоугольного параллелепипеда, которые нам, не понятно откуда, известны по условию.

Как найти угол по тангенсу

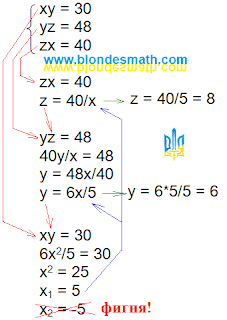
В комментариях к тригонометрической таблице меня спросили, как перевести в градусы tg@= 4,99237? В общем виде вопрос заключается в том, как найти угол по тангенсу? Для решения этой задачи мы будем использовать калькулятор. Поскольку математики никогда не ставили перед собой задачи навести порядок в математике, то углы и сегодня измеряются в самых разных единицах измерения. Наиболее популярны среди математиков градусная и радианная меры углов. Мы тоже найдем решение как в градусах, так и в радианах. Благо, на калькуляторе они есть.

Как включить калькулятор? Читайте в конце этой страницы.

Сначала мы найдем угол по тангенсу в градусах. Для этого в правом верхнем углу калькулятора нужно установить специальный пыптик в положение Deg 360, что соответствует градусам. Дальше кнопочками вводим число 4,99237. Вот что у нас должно получиться.

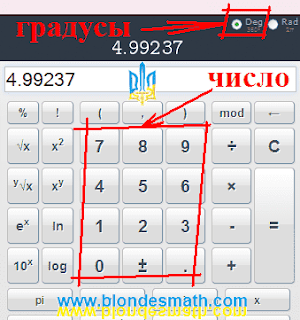Как найти угол по тангенсу. Шаг 1.

После этого нужно нажать кнопочку арктангенс. Именно эта математическая ерунда превращает значение тангенса в угол. На калькуляторе эта хитрая обратная тригонометрическая функция (как её величают математики) замаскирована под кнопочку tan в степени минус 1, то есть тангенс в минус первой степени. После нажатия этой кнопочки восторженный калькулятор на все лады расхваливает нашу мудрость и всеми возможными способами сообщает нам, что мы таки ковырнули арктангенс, а не что нибудь другое. Об этом свидетельствует название функции atan (4.99237) в окошке калькулятора. Для особо одаренных здесь же буковками написано Arc tangent. Правда, особо одаренным нужно ещё знать английский язык, для того, чтобы понять всю глубину восторга калькулятора.

Как найти угол по тангенсу. Шаг 2.

"А где же угол?" - спросите вы и будете правы. Угла нет, не смотря на все наши старания. Для превращения восторга калькулятора в математический результат нужно ещё нажать здоровенную кнопку равно, обозначенную двумя горизонтальными палочками =. Вот теперь мы нашли угол по тангенсу в градусах. Он равняется 78,6732 (ну, и так далее) градусов.

Как найти угол по тангенсу. Шаг 3.

Для полного счастья, можно пролить бальзам на душу математиков, разложив эту десятичную форму записи градусов на градусы, минуты и секунды. Для этого дробную часть числа умножаем на 60 и получаем количество минут в дробном хвосте градусов.

0,6732 * 60 = 40,392'

Подобную процедуру повторяем с минутами. Дробную часть минут умножаем на 60 и получаем секунды.

0,392 * 60 = 23,52"

Процедуру можно повторять и дальше до бесконечности, но, к счастью, математики до этого ещё не додумались. По этому на секундах мы и остановимся. Ничего, что секунды у нас получились с дробным хвостиком. Математики к таким хвостам относятся терпимо. В итоге, полнометражная версия полученного нами угла в градусной мере углов выглядит следующим образом:

78 градусов 40' 23,52"

В слух эта магическая надпись произносится так: "78 градусов, 40 минут, 23 целых и 52 сотых секунды". Аминь!

Нет, ещё не "Аминь!". Теперь нужно выковырять из калькулятора этот же угол, только в радианах. Процедура добывания угла точно такая же, как и для градусов, с той только разницей, что в самом начале мы на калькуляторе нажимаем соседний пыптик Rad 2п. Повинуясь нашей воле, калькулятор добросовестно выдаст нам результат в радианах. Вот как это будет выглядеть.

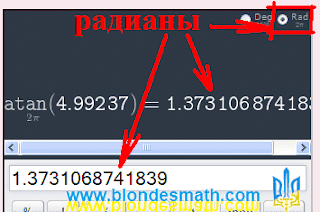Как найти угол по тангенсу. Угол в радианах.

Как видите, в радианах мы получили всего-навсего 1,3731 радиан. И за что математики так любят радианы? Ведь, плюнуть не на что. Ну, да Бог с ними, с этими математиками.

Тетерь самый интересный вопрос из комментариев: "А как включить-то калькулятор???"

Теоритически, на всех компьютерах и смартфонах калькулятор устанавливается по умолчанию. Просто его нужно найти.

Компьютер. Нажимаем кнопку "Пуск", затем нажимаем "Все программы". Ищем среди программ "Стандартные" и открываем эту папку. У меня именно в ней спрятана программа "Калькулятор". Открываем эту программу нажатием левой кнопки мыши, появляется калькулятор. Если вы не видите на калькуляторе тангансов, котангенсов и прочей математической ерунды, тогда в верхнем меню нажмите на слово "Вид" и включите пиптик "Инженерный". Ваш калькулятор готов к великим математическим свершениям. Кстати, по логике разработчиков калькуляторов, вся эта математическая ерунда типа тангенсы-котангенсы обычным людям и даром не нужна, о чем всидетельствует "Обычный" вид калькулятора.

Смартфон. У меня калькулятор расположен прямо на главном экране. Нажимай и пользуйся. Вот только вылезает калькулятор в обычном виде. Где найти математику? Никогда не задавался таким вопросом. Методом научного тыка выяснил, что в левом нижнем углу экрана есть красненький значек, изображающий два какдратика по диагонали и две стрелочки. После нажатия на этот символ появляются все математические фишки, заложенные разработкичами. Теперь вы становитесь повелителем тангенсов-котангенсов и прочих математических чудес.

Попробую сделать отдельную страницу, посвященную калькулятору, где будут картики и разные полезности. Метод научного тыка - не самый эффективный научный метод, гораздо разумнее пользоваться информацией, которую раздобыли другие пользователи.

sin x с минусом

Тут меня заграничные блондинки попросили решить один пример, в котором sin x с минусом. Хоть английского я не знаю, но язык математики в некоторых местах понимать умею. Нужно найти значение икса в пределах от 0 до 360 градусов с градусами, минутами и секундами, если синус икс равен минус 0,8453. В принципе, математика везде одинаковая, по этому и задачи всем задают похожие. Посмотрим, как это выглядит.

sin x = -0,8453

Картинки, с вашего позволения, я использую те же, что рисовал для иностранных блондинок. Так будет быстрее. Прежде всего, определимся с тем, что от нас требуется. Если синус угла равняется какому-то числу, то зная какое-то число, можно найти угол, синус которого будет равняться этому числу ... в доме, который построил Джек! То есть, нужно не по углу искать число, а по числу - угол. Да, буквой икс в математике могут обозначать не только неизвестное число, но и неизвестный угол. Проблема заключается в том, что тригонометрических таблиц с отрицательными значениями синусов и косинусов математики не составляют - суеверия у них такие. При решении подобных задач мы, как и математики, будем пользоваться имеющимися у нас знаниями.

Как математики не обращают внимания на окружающую действительность, так и мы, в начале, не будем обращать внимания на знак минус перед числом. Возьмем тригонометрическую таблицу синусов (она же таблица Брадиса) и найдем в ней число 0,8453. По этому числу мы можем найти угол, синус которого ... в доме, который построил Джек! Этот угол находится в пределах от 0 до 90 градусов и равняется он 54 градуса 42 минуты. Обозначим этот, промежуточный в расчетах, угол через a.

sin x с минусом

На картинке промежуточный угол я обозначил через х вместо a. Вот так выглядит старческий склероз. Кстати, самая лучшая в мире болезнь - ничего не болит и каждый день новости.

sin а = +0.8453

а = 57 градусов 42 минуты

Дальше мы сморим тригонометрический круг и находим угол a. Положительные значения синуса расположены в верхней половине круга, отрицательные - в нижней половине.

sin x с минусом

Одному значению синуса всегда соответствует два значения угла. Найдем эти углы для отрицательного значения синуса a.

sin x с минусом

Первый угол мы получим, если к углу а прибавим 180 градусов. Второй угол получается, если из 360 градусов вычесть угол а.

x1 = 180 градусов + a

x1 = 180 градусов + 57 градусов 42 минуты

x1 = (180 + 57) градусов 42 минуты

x1 = 237 градусов 42 минуты


x2 = 360 градусов - a

x2 = 360 градусов - 57 градусов 42 минуты

x2 = 359 градусов 60 минут - 57 градусов 42 минуты

x2 = (359 - 57) градусов (60 - 42) минуты

x2 = 302 градуса 18 минут

Это было пояснение, как найти sin x с минусом. Теперь это решение нужно записать в соответствии с бюрократическими правилами, которых я не знаю. Выглядит решение приблизительно так.

sin x = -0.8453

x = arcsin (-0.8453)

x1 = 237 градусов 42 минуты

x2 = 302 градуса 17 минут

Надеюсь, теперь всё. Вот!