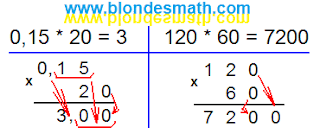Квадрат и призма

Задача про квадрат и призму. Точнее, про один квадрат и две призмы. Вот что нам предлагают сделать:

Квадрат со стороной 24 см в первый раз свернут в виде боковой поверхности правильной треугольной призмы, а во второй раз – в виде правильной четырехугольной призмы. Сравните объемы этих призм.

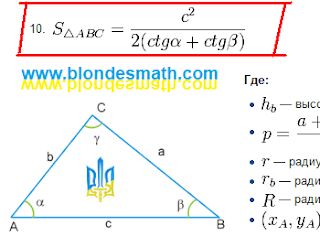
Так, о чем говорится в этой задаче? В ней говорится о правильных треугольной и четырехугольной призмах, боковая поверхность которых (в развернутом виде) представляет собой квадрат размером 24 на 24 сантиметра. Вот как выглядят эти призмы.

Квадрат и призма

Как сравнить объемы таких призм? Нужно объем одной призмы разделить на объем другой призмы. Для разных призм существует много разных формул определения их объема. Но есть одна формула, одинаковая для всех призм и цилиндров: объем равен площади основания, умноженной на высоту призмы или цилиндра. Для начала разберемся с высотой.

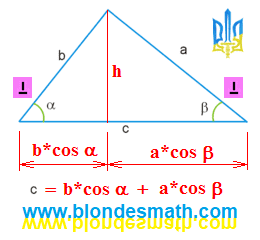
Если мы свернем наш квадрат в трубочку, длина трубочки будет равна длине стороны квадрата, то есть 24 см. Если мы этот же квадрат изломаем в призму, высота этой призмы (любой) будет равна 24 см (сторона квадрата). И так, наши призмы имеют одинаковую высоту. При сравнении объемов таких призм на результат влияет только площадь основания, высота в формулах объемов сократится. Баба с возу - кобыле легче. Или высота из формулы - формула проще.

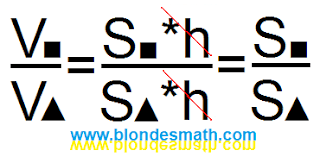Квадрат и призма

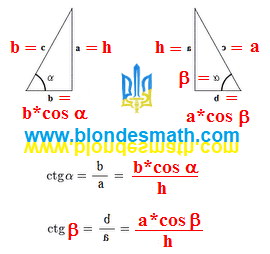
Теперь нужно разобраться с правильными треугольниками и четырехугольниками. Правильным треугольником математики называют равносторонний треугольник, правильным четырехугольником - квадрат. Именно эти две фигуры являются основаниями наших призм. Нам нужно сравнить их площади. С площадью квадрата всё понятно – она равна длине стороны квадрата во второй степени. Для площади равностороннего треугольника есть свои формулы. Нагло идем в Википедию, типа мы ищем "правильный треугольник", и тырим формулы там.

Квадрат и призма

Нам нужна первая формула площади правильного треугольника. Как быть с длинами сторон треугольника и квадрата в основании призмы? Развертка боковой поверхности призмы представляет собой квадрат. Длина одной стороны этого квадрата равна периметру основания, а вторая сторона квадрата равна высоте призмы. У треугольника периметр равен трем длинам сторон, у квадрата – четырем. Разделим 24 сантиметра на три и на четыре части. Мы получим, что длина стороны правильного треугольника (равностороннего) равняется 8 сантиметров, длина стороны квадрата равняется 6 сантиметров. На картинке пунктиром показаны линии изгиба.

Квадрат и призма

Теперь подставим длины сторон в формулы площадей и найдем их отношения. Поскольку отношение может быть и "круть-верть", и "верть-круть", запишу для вас оба варианта. Один из этих вариантов точно будет в ответах (если ответы на задачи у вас есть, не все обладают таким счастьем).

Квадрат и призма

В первом случае мы площадь квадрата делим на площадь треугольника, во втором случае площадь треугольника делим на площадь квадрата. В результате получаем две взаимно обратные дроби - переворачиваем вверх тормашками одну дробь и получаем другую.

Прямоугольный параллелепипед перпендикулярные ребра

Очень важной составляющей при изучении математики является воображение. Особенно, при изучении геометрии. Вот, например, задача про прямоугольный параллелепипед и его перпендикулярные ребра:

На прямоугольном параллелепипеде ABCDA1B1C1D1 указать общий перпендикуляр прямых A1D1 и BB1.

Для решения этой задачи про параллелепипед предлагаю отправиться в воображаемое путешествие. Это мои ассоциации между задачей про параллелепипед и окружающей реальностью. Уж какая реальность, такие и ассоциации.

Каждый школьник хотя бы раз в жизни должен совершить Священный Круг вокруг прямоугольного параллелепипеда и будет ему за это отличная оценка... может быть, когда нибудь. ...И это смутно мне напоминает одну из основных религий мира...

Подходим к нашей Святыне (прямоугольный параллелепипед) и смотрим. ВВ1 явно является вертикальным ребром. Нужное нам ребро A1D1 расположено где-то сверху горизонтально. По всем канонам исповедуемой нами религии (математики), свой обход мы должны совершать в строго определенном порядке. Начинаем с точки А1 и идем в сторону В1. После того, как ребро А1В1 закончилось, поворачиваем под прямым углом и идем вдоль ребра В1С1. Поворачиваем под прямым углом. Проходим ребро C1D1, поворачиваем. Вот теперь мы идем вдоль ребра D1А1. Идем мы в сторону, противоположную указанной проповедниками математики (A1D1), но на оценку это не влияет. И вот здесь мы должны совершить поворот на 90 градусов, чтобы снова пойти вдоль ребра А1В1...

Прямоугольный параллелепипед перпендикулярные ребра

Вот оно, то самое ребро, из которого мы можем сотворить ответ на задачу, как когда-то Бог сотворил женщину (блондинку или брюнетку?)! Ребро А1В1 перпендикулярно одновременно ребру A1D1 в горизонтальной плоскости и ребру ВВ1 в вертикальной плоскости. Это ребро начинается в вершине А1 и заканчивается в вершине В1, а, следовательно, является общим перпендикуляром к этим двум прямым! Святой Грааль задачи найден! Аминь! Или "плюс константа"? Нет, константа - это из Евангелия от Интеграла. А у нас сегодня Евангелие от Стереометрии.

Можете верить во что угодно, но... Лично я не советую верить тем, кто обещает вам что-нибудь сразу после того, как вы... заплатите, проголосуете, умрете (нужное подчеркнуть).

Квадратное уравнение решение онлайн

Не легкая сегодня жизнь у учащихся. Для её облегчения предлагаю вашему вниманию калькуляторы уравнений: квадратное уравнение решение онлайн. Надеюсь, этот калькулятор поможет вам в решении квадратных уравнений. Продавцам оценок без разницы, а вот учителя требуют ещё и определение квадратного уравнения знать. Вот оно на картинке.

Квадратное уравнение

Распечатайте картинку, повесьте её на стену и каждый вечер читайте на ночь вместо молитвы. Подобные ежедневные упражнения очень здорово помогают превращать запор мысли в понос слов. Последнее предложение я вычеркнул специально. Детям его знать ещё рано, а взрослым оно не нужно вообще. Лично я тем математикам, которые выдают комплексные решения, платил бы комплексную зарплату: действительная часть равна минимальной зарплате, а в комплексной части зарплаты можно обещать всё, что угодно. Хоть Царство Небесное. Естественно, не здесь и сейчас, а где-то там и после смерти. Ведь мертвые никогда не требуют выполнения обещаний.

Но вернемся к нашим уравнениям. Квадратное уравнение является уравнением второго порядка. У квадратного уравнения есть своя формула, которую вы можете видеть на картинке. Если подходить к написанному на картинке с позиции тупой бюрократической функции, то икс не является корнем квадратного уравнения. Это переменная. Корнями квадратного уравнения являются определенные числовые значения переменной икс. При подстановке корней в квадратное уравнение оно должно превращаться в верное равенство. У квадратного уравнения может быть два корня (разные числа, возведенные в квадрат, могут давать одинаковый результат; знаки плюс и минус делают числа разными), один корень или квадратное уравнение может вообще не иметь корней. Последние уравнения, не имеющие корней, я бы назвал "плохое квадратное уравнение". Правильно составленное квадратное уравнение всегда должно иметь решение. Здесь мы упираемся в очень неудобный и интересный вопрос: откуда берутся квадратные уравнения и зачем они нужны? Уравнения ради решений - это маразм или дрессировка обезьян (воспитание тупых бюрократических функций, пригодных для использования в любых бюрократических системах). Уравнения как математический инструмент? Тогда где и как этот инструмент применяется? Квадратное уравнение, взятое с потолка (как это обычно делается для учебников), может не иметь решений. Ведь на правильность составления нас уравнения проверять не учат. Тупо пишем квадратное уравнение в учебник, тупо берем из учебника и решаем.

Дискриминант квадратного уравнения применяется для нахождения его корней. Дискриминант равен квадрату второго коэффициента минус четыре произведения первого коэффициента и свободного члена уравнения. Если дискриминант больше нуля, тогда уравнение имеет два корня. Если дискриминант равен нулю (дискриминант 0), тогда квадратное уравнение имеет всего один корень. Если дискриминант меньше нуля, тогда уравнение не имеет корней - это уравнение взял с потолка какой-то неук.

Теперь рекомендую вашему вниманию специальные калькуляторы для решения квадратный уравнений онлайн с подробным решением:

Квадратное уравнение решение онлайн с графиком

- дается подробное решение с формулой дискриминанта, с графиком уравнения и анализом вершин кривой.

Квадратное уравнение решение онлайн

- пример подробного решения уравнения на этом калькуляторе вы можете видеть на картинке ниже.

Квадратное уравнение решение онлайн

Решатель уравнений онлайн

- этот сервис решения квадратных уравнений онлайн выдает просто корни уравнения без подробного решения, но зато может представить их в виде квадратных корней (как на картинке ниже). Обратите внимание, что примеры введения уравнений и систем уравнений в этот калькулятор уравнений приведены внизу и несколько отличаются от традиционно принятых наборов символов. В этом калькуляторе квадрат икса нужно вводить как произведение двух иксов.

Квадратное уравнение решение онлайн

P.S. 30.03.23г. Как ни странно, но все три сайта пережили потрясения и продолжают исправно работать. Создателям респект.

Площадь треугольника через котангенс

Сейчас мы разберемся, как находить площадь треугольника через котангенс, точнее, рассмотрим вывод формулы. Как выглядит площадь треугольника при вычислении её через котангенс? Вот так.

Площадь треугольника через котангенс

Всем нам известно, что площадь треугольника равна половине произведения основания на высоту. Куда девается высота и откуда появляются котангенсы в этой формуле? Как получить эту формулу? Рецепт довольно прост, как в кулинарии. Нужно взять необходимые компоненты этого математического блюда, предварительно их подготовить и из полуфабрикатов приготовить саму формулу. Продукты для еды мы покупаем в магазине. Где брать составные компоненты математической формулы? Треугольник у нас уже есть. Еще нам понадобится определение котангенса через треугольник. Берем на указанной странице картинку и вырезаем необходимые компоненты.

Котангенс

Теперь начинаются работы по предварительной подготовке к процессу выведения формулы. Как и на кухне, нужно всё соответствующим образом подготовить - почистить, нарезать, поджарить, отварить... Короче, вы гораздо лучше меня знаете, что нужно делать на кухне. Я умею только покушать.

Площадь треугольника через котангенс

Убираем из рисунка всё лишнее. Красным цветом я дорисовал то, что нам будет нужно. Высота треугольника входит в площадь треугольника. Она делит основание на два отрезка. Длинна каждого отрезка определяется как проекция на основание выше расположенной стороны треугольника. Пользуясь портретом тангенса, я без труда определяю, что использовать нужно косинусы углов. Запишем формулу основания как сумму двух проекций сторон. Переходим к картинке котангенса.

Площадь треугольника через котангенс

Теперь с картинки треугольника нам нужно перенести все обозначения на картинку котангенса. С левым углом никаких проблем нет, на обеих картинках они направлены в одну сторону. Используя старые обозначения в формуле котангенса и знак равенства на картинке, мы без труда получаем формулу котангенса угла альфа для нашего треугольника. А вот с углом бета возникли маленькие проблемы. Он смотрит в другую сторону. Не отчаиваемся. Как заправские спецназовцы, берем картинку с углом альфа и проводим операцию "фейс даун", то есть кладем её мордой в пол. Надеваем на неё наручники и подносим к окну. Сквозь лист бумаги проступает расплывчатый рисунок... Вау! Да это же тот самый угол, который нам нужен! А притворялся другим углом (в кулинарных рецептах вы подобных приемчиков не найдете, но ведь и математика - не кулинария). Ставим свои обозначения на перевернутой картинке и получаем значение котангенса угла бета.

Всё. Теперь приступаем к приготовлению самого блюда, то есть к выведению формулы площади треугольника через котангенсы двух углов альфа и бета. Повторяю, что начинаем мы с общей формулы, где площадь треугольника равна половине произведения основания на высоту. Записываем всё раздельно: половинку, основание и высоту. Потом с высотой начинаем выполнять волшебные превращения в строгом соответствии с уже полученными нами формулами.

Площадь треугольника через котангенс

В конце полученное нами значение высоты треугольника, выраженное через котангенс, подставляем в первую формулу и слепливаем всё в кучку. Как видите, ничего сложного в этом рецепте нет.

Общая рекомендация при выведении других формул. Смотрите, что у вас есть в начале и в конце. Ищите то, чем это можно связать вместе. В нашем случае начало и конец связываются определением котангенса через треугольник.

Система неравенств пример

Сейчас мы рассмотрим, как решается система неравенств пример. Что такое система неравенств? Это несколько неравенств, связанных между собою одним неизвестным. Для каждого неравенства в отдельности нужно найти значения неизвестного. Потом из этой кучки значений нужно выбрать те значения, которые удовлетворяют все неравенства системы одновременно. То есть, подставив одно такое значение неизвестного сразу во все неравенства, мы получим шикарный набор правильных числовых неравенств.

На примере с блондинками это будет выглядеть так. У нас есть две блондинки. У каждой из блондинок есть желание. Применяя всякие хитрые методы дознания, типа "А вот чего бы ты хотела?", выясняем, что одна блондинка хочет кататься, вторая блондинка хочет к воде. Есть ли решение у этой системы из двух блондинок? Да, таких решений множество. Одновременно удовлетворить желания двух блондинок могут: катание на лодке, катание на катере, катание на яхте, катание на круизном океанском лайнере... Катание на подводной лодке среди коралловых рифов тропического моря можно считать эквивалентом математической бесконечности.

Система неравенств может и не иметь решения. Действительно, попробуйте ещё найти таких блондинок, желания которых можно удовлетворить одним махом. Тем более, у каждой блондинки в запасе всегда имеется фраза типа "Я передумала". Таких блондинок мы называем капризными. К нашему величайшему счастью, капризных неравенств математики ещё не придумали.

Теперь отвлечемся от блондинок и займемся математикой. Вот наша система неравенств и вот пример того, как она решается.

Система неравенств пример

И так, для решения системы неравенств в нашем примере, мы берем каждое неравенство в отдельности и упрощаем его до невозможности упрощать дальше. Первое неравенство (зелененькое) упрощается практически так же, как любое математическое выражение - жонглируем числами до получения значения икса в чистом виде. Во втором неравенстве (синеньком), кроме жонглирования, мы применяем умножение неравенства на минус единицу. При этом знак "меньше" у нас меняется на знак "больше".

После этого берем результаты и смотрим, какое из этих решений будет удовлетворять оба неравенства одновременно. Первое решение не подходит, поскольку значения икса на промежутке от 5 до 8 не являются решением второго неравенства. Второе решение подходит и для первого неравенства, и для второго. Следовательно, решением системы неравенств в нашем примере будет икс больше восьми. Внизу картинки показан пример графического решения этой системы на числовой оси.

Знак больше и меньше

Здесь мы рассмотрим элемент математического неравенства, при помощи которого в математике обычно выражается несправедливость. Если знак равенства можно считать отражением справедливости, то знаки "больше" и "меньше" отражают отсутствие таковой. Справедливость - это понятие относительное. То, что я считаю справедливым по отношению к вам, вы можете считать не справедливым по отношению к себе. И наоборот. То, что считаете справедливым вы, другие могут называть вопиющей несправедливостью. Каждый смотрит со своей колокольни. В математике всё это можно выразить при помощи знаков "больше" и "меньше".

Наблюдая за процессом сравнения со стороны, мы будем получать разные результаты в зависимости от того, в каком порядке мы выполняем сравнение. Небоскреб БОЛЬШЕ хибарки. Хибарка МЕНЬШЕ небоскреба. Как видите, результат сравнения зависит от того, что мы ставим на первое место при сравнении.

В математике неравенство возникает из-за того, что при записи математических выражений принят определенный порядок выписывания символов на бумаге. При этом один из символов обязательно будет на первом месте, второй символ - на втором. Это приводит к определенному результату при сравнении того, что эти символы обозначают. Если мы изменим порядок записи символов, то есть второй символ запишем на первом месте, а первый - после него, тогда у нас изменится результат сравнения. Математики очень удачно подобрали графические символы для обозначения понятий "больше" и "меньше". Вот так выглядят знаки БОЛЬШЕ и МЕНЬШЕ в математике.

Знаки больше и меньше

Есть разные уловки для запоминания этих знаков. Вот один из способов, как запомнить знаки больше и меньше.

Что такое неравенство? Это почти то же самое, что и уравнение, только вместо знака "равно" ставится знак "больше" или "меньше". Решаются они практически одинаково. Единственное, о чем нужно помнить при решении неравенств, что знаки "больше" и "меньше" могут выворачиваться на изнанку, а знак равенства - нет. Собственно, знак равенства тоже можно вывернуть, но никаких отличий вы не увидите. Другое дело со знаками "больше" и "меньше". Если такой знак вывернуть на изнанку, тогда его нос будет смотреть в другую сторону. Знак "больше" превратится в знак "меньше", знак "меньше" превратится в знак "больше".

Никакой шаманской магии в этом нет. Обыкновенная относительность или, как её ещё называют в математике, зеркальная симметрия. Посмотрите на рисунок ниже.

Знак больше и меньше

Нижняя половина рисунка является зеркальным отражением верхней половины. Или наоборот. Теперь возьмите зеркало. Приставьте его перпендикулярно к экрану монитора так, чтобы одновременно видеть картинку на экране монитора и её отражение в зеркале. В зеркале нижняя и верхняя половины картинки поменяются местами. Если бы не надпись на картинке "математика для блондинок", то вообще нельзя было бы точно сказать, где сама картинка, а где её отражение. Кстати, применение на уроках математики прозрачной стеклянной доски, вращающейся вокруг вертикальной оси, поможет понять очень многие вещи в математике.

Так вот, если мы в математическом неравенстве меняем местами левую и правую части неравенства, то знак меняется на противоположный. Знак "больше" меняется на знак "меньше" и наоборот. То же самое происходит, когда мы умножаем всё неравенство на минус единицу. При этом меняются все знаки в левой и правой частях неравенства. Умножение на минус единицу мы можем использовать при решении неравенств.

Нужно помнить, что если мы переносим всего один элемент из одной части неравенства в другую и при этом МЕНЯЕМ ЗНАК "плюс" или "минус", то знак неравенства "больше" или "меньше" остается неизменным. Всё, как в уравнении. Если при переносе математического элемента через знак сравнения мы изменяем знак, результат сравнения не изменяется: равенство сохраняется, знак "больше" остается знаком "больше", знак "меньше" остается знаком "меньше".

Порядок действий в математике пример

В порядке оказания скорой математической помощи, решим тестовое задание для 5 класса. В этом тесте мы рассмотрим порядок действий в математике пример. У нас имеется набор математических действий с двумя парами скобок. Как решить такой пример? Сперва выполняем действия во внутренних скобках. После их выполнения внутренние скобки у нас исчезают и вместо них мы получаем число. Дальше выполняем математические действия в оставшихся скобках (в начале они были наружными скобками). В заключение операции "Порядок действий в математике" выполняем всё то, что осталось за скобками.

При всех наших вычислениях в скобках строго соблюдаем незыблемое правило выполнения математических действий: сперва выполняем умножение и деление, только после этого выполняем сложение и вычитание. Если что-то из этого отсутствует - радуйтесь!

Теперь рассмотрим сам пример и порядок действий.

Порядок действий в математике пример

В самом начале рассматриваем внутренние круглые скобки. В них спрятаны вычитание и умножение. Первым действием выполняем умножение (деления нет - ура!), вторым - вычитание. С первой парой круглых скобок мы покончили. Но у нас остается ещё одни пара скобок, в которой есть деление, сложение, умножение. Прежде, чем выполнять сложение, необходимо выполнить деление и умножение. В какой последовательности выполнять эти два действия в данном примере - принципиального значения не имеет. Мы выполним по порядку - сперва деление, потом умножение. Полученные в результате числа складываем. В завершение всех мучений выполняем деление. Результат можно записать в виде числа с десятичной дробью (боюсь, что данное замечание не касается учеников пятых классов - сам-то я там не учусь), но обыкновенная дробь выглядит гораздо круче.

В нижней строчке решенный нами пример записан в несколько ином, более фотогеничном, виде. Различные формы записи математического выражения на порядок выполнения действий не влияют. Если, конечно, мы всё правильно записали.

Как порядочный лентяй, при решении этого примера я воспользовался математическим калькулятором (был калькулятор и исчез, только инструкция по применению осталась), в который просто ввел выражение (41811/1267+506*(3000-2*877))/153 и нажал кнопочку "равно". Подробного решения этот калькулятор онлайн не дает, но правильный ответ подсмотреть можно.

Ещё вам может очень пригодиться разложение числа на множители онлайн при сокращении дробей. Называется данная операция очень страшно: "Факторизация числа". Естественно, у меня возникает вопрос: чем разложение чисел на множители отличается от факторизации числа? Разложением чисел на множители занимаются дети в школе. Скорее всего, взрослым дядькам стыдно этим заниматься, поэтому они с умным видом занимаются факторизацией чисел (чем бы дитя не тешилось - лишь бы не плакало).

Производная функции онлайн

Это презентация специального калькулятора, для которого производная функции онлайн является самой простой задачей, которую только вы можете придумать. Если вам не терпится найти производную функции, которая, вне всякого сомнения, является вашей любимой математической функцией, тогда быстрее переходите по ссылке:

производная функции онлайн

Мы же немножко порассуждаем о производных функции онлайн и о нашей действительности. И так...

Если вы оказались на этой странице, значит вы где-то учитесь. Рядовой обыватель никогда в жизни не станет искать в Интернете производную функции онлайн, разве что под страхом пыток. Для учащихся мы совершим беглую экскурсию по сервису онлайн производных, который вам здесь рекомендуется.

Сейчас мы не будем вдаваться в определение производной, которое придумали математики. Наша задача взять ту функцию, которую нам задали математики и найти производную функции, что бы могли отмахнуться этим решением от математиков, как от назойливых мух. И так, мы имеем сервис, который позволяет найти производную и частную производную в режиме онлайн. В этом сервисе есть специальное окошко для ввода значения функции.

Производная функции онлайн

То, что вы сейчас видите на картинке, получено мною при помощи ссылки "Переключить на компактный дизайн". Есть там такая в самой верхней строчке сервиса, рядом с выбором языков. Не знаю, как у вас, а у меня именно такая функция вылезает по умолчанию. Помимо этого, в самом калькуляторе производных имеется кнопочка "Редактор" (у меня она не работает, выдает ошибку Джава-скрипта) и кнопочка "Предварительный просмотр". К имеющейся функции я добавлю что-нибудь от себя прямо в окошке и нажму на кнопку предварительного просмотра.

Производная функции онлайн

Умный калькулятор покажет нам, как именно он понял то, что мы пытались в него впихнуть. Введенную нами функцию в компьютерном выражении калькулятор преобразует в математическое выражение. Следует заметить, что общение с калькулятором пределов основано на всеобщем математическом равенстве: калькулятору абсолютно безразлично, кто с ним общается - двоечник из 5-Б класса или профессор математики - все должны выражать свои мысли на языке компьютера, а не на своем собственном. Иначе калькулятор вас понимать откажется.

В качестве бонуса предлагаются дополнительные опции. Можно найти обычную производную функции одной переменной, можно найти частную производную по "х", частную производную по "у" - это функции двух переменных (наверное, это и есть производная сложной функции). Можно поставить галочку возле автоматического распознавания констант или автоматически использовать линейность производной. Что-то типа:

- Официант! Мне одну порцию производной, пожалуйста.
- Вам с линейностью или без?
- А у вас линейность свежая?
- Только сегодня утром завезли, прямо с грядки. Очень рекомендую! Наша линейность выращивается на экологически чистом числовом поле.
- Уговорили, давайте производную с линейностью.

Теперь о самом интересном - решение производных. Нажимаем кнопочку "Отправить", ждем несколько секунд и получаем решение производной. Оно выдается на отдельной странице в формате pdf. Это такой специальный формат картинки, которую можно распечатать и отмахиваться этим листком от математиков. Решение производных расписано очень подробно, шаг за шагом. В конце предлагается несколько вариантов упрощения полученного выражения. Выглядит всё это приблизительно так.

Производная функции онлайн решение

Как видите, решение производных расписано очень подробно. Здесь используются формулы производной степенной функции, производная произведения двух функций, производная экспоненциальной функции. Упрощение выражения может быть выполнено и до взятия производной. Об этом есть предупреждение в самом низу страницы. Так что не пугайтесь, если в исходных данных для получения производной онлайн вы увидите совсем другую функцию.

Подводя итог, можно сказать, что данный калькулятор производных избавляет нас от необходимости ломать голову в поиске решения производной. Тупо вставили функцию, тупо получили производную, переписали решение, ткнули в нос математику и забыли навсегда. Возникает вполне естественный вопрос: зачем учить всю эту фигню, если есть калькулятор производных? Это только гурманы-математики могут пытаться найти ошибки в решениях калькулятора.

Чего нет у тригонометрических функций

Автор Николай Хижняк

Не научные, но фантастические приключения блондинок с элементами реализма. Продолжение рассказа о том, что такое математика и физика.

- А разве у тригонометрических функций чего-то может не быть? – удивились блондинки.

- Да, сейчас я вам перечислю то, чего нет у тригонометрических функций, но нас уверяют, что оно есть, – это знаки, периодичность и углы больше 90 градусов.

- Куда же они деваются? – пошли в наступление блондинки.

- Их там никогда не было. Где у прямоугольного треугольника знаки плюс и минус? Где периодичность гипотенузы? Как у прямоугольного треугольника может появиться угол больше 90 градусов, когда один такой угол уже есть, а сумма углов треугольника не может быть больше 180 градусов? При всём этом тригонометрические функции на прямоугольном треугольнике определяются легко и просто. Собственно, это и есть математическое доказательство отсутствия у тригонометрических функций знаков, периодичности и тупых углов.

- Я что-то не поняла, кто тупой – вы или математики? – лицо блондинки, задавшей этот вопрос, выражало святую невинность.

- Девочки, вы не правильно формулируете вопрос. Здесь речь идет не о дураках и умных, а о верующих и не верующих.

- Упс, – выдохнула блондинка, – причем здесь вера?

- Очень даже причем. Вам в школе и в институте рассказывали что-то о тригонометрических функциях, и вы в это поверили. Сейчас вы продолжаете верить своим учителям математики, а ваши учителя верят в математические определения. Я в определения не верю и вам не советую. Я верю только в результат. Тригонометрические функции на треугольнике дают совсем не тот результат, о котором говорится в определении тригонометрических функций. Математики, как и все верующие, видят только те результаты, которые подкрепляют их веру, и полностью игнорируют то, что противоречит их вере.

- Так это что получается? – озадаченно спросила одна из блондинок, – Математика – это религия, а не наука?

- Получается так. Ни христианам, ни мусульманам, даже при помощи самого кровавого террора, не удалось сделать то, что сделали математики – они завоевали весь мир. Сегодня даже мусульмане, благодаря математикам, смотрят на окружающую действительность сквозь Святой Крест Декартовой Системы Координат. Кстати, от средневековой Инквизиции всем нам пламенный привет.

- А причем здесь Инквизиция? – удивились блондинки.

- История математики – это не только даты и фамилии ученых, но и события с их последствиями. Подробнее об истории математики я вам расскажу как-нибудь в другой раз. Сейчас давайте со стороны посмотрим на результат. Что такое математические определения? Это те же Библейские тексты, в которые нужно верить. Что такое теория множеств? Это наследие легендарного Библейского Ноя – каждой твари по паре. Что такое математические функции? Это то, что мы видим сквозь Святой Крест Декартовой Системы Координат. Что такое комплексное пространство? Это Царство Небесное. Ни комплексного пространства, ни Царства Небесного никто никогда не видел, но все верят, что они есть. Во всяком случае, в этом нас уверяют проповедники математики и религии. Как видите, в исторической борьбе с наукой победила средневековая европейская Инквизиция при помощи математики. Думаю, о такой безоговорочной победе не только над учеными, но и над конкурентами, инквизиторы даже в самых сладких снах не мечтали.

- Ужас, – только и смогли сказать блондинки.

- Та математика, которой учат нас математики – это математика рабов Божьих. «Пусть нам дано…», «Возьмем…» любимые выражения математиков. Эти выражения подразумевают, что всё создано Богом для нас и мы можем этим только пользоваться. Мы же с вами будим изучать математику Богов. Нам самим придется решать, что у нас есть, и какой результат мы можем из этого получить. В чем разница? – подавленные блондинки никак не отреагировали на провокационный вопрос, - Вот пример из тригонометрии. Об обратных тригонометрических функциях вы помните?

- Ну так, смутно, – вяло признались блондинки.

- Это когда по числу нас заставляли искать угол. При этом математики нам всегда говорят, какую именно обратную тригонометрическую функцию мы должны использовать: арксинус, арктангенс… А что делать, если мы имеем только число и нам нужно получить угол? Сперва нужно определить тип тригонометрической зависимости, в результате которой появилось это число, а уже потом искать угол. В окружающей природе нигде нет бирочек с названиями тригонометрических функций.

- Так нам что, бирочки придется развешивать? – уныло спросила одна из блондинок.

- В каком-то смысле – да. Вы же хотите быть богинями? – решил я поднять настроение блондинок.

- Да как-то уже не очень… – честно призналась одна блондинка, вторая задумчиво спросила, – А как математикам удается решать все те задачи, которые им подсовывают, если математика – это религия?

- Здесь ничего сложного нет. Когда есть условие задачи, когда приблизительно известен нужный результат, то составить решение, соответствующее принятым определениям не составляет большого труда. Тем более что математикам, в отличие от религиозных проповедников, разрешается самим дописывать новые определения, не противоречащие старым. Математики сами пишут свою Библию, в которую потом верят сами и заставляют верить других. Так вот я в эту математическую Библию не верю. Вернемся к началу нашего разговора о дураках и умных. Я не считаю математиков дураками. Просто я и математики верим в разные вещи. Являюсь ли дураком я сам? Это решайте вы.

Блондинки молча смотрели на меня, пытаясь оценить мои умственные способности. Задача для них была явно не простой.

- Давайте на этом будем заканчивать, – сказал я, – В следующий раз мы с вами познакомимся с тригонометрическими функциями. Тогда вам будет гораздо проще понять, откуда берутся те вещи, которых нет у тригонометрических функций…

- А разве треугольник – это не тригонометрические функции? – удивленно спросили блондинки.

- Нет. Треугольник – это место, в котором тригонометрические функции добросовестно работают, как и в тригонометрическом круге. Но рождаются и живут тригонометрические функции совсем в другом месте.

Закончить наш разговор о тригонометрических функциях мы так и не смогли. Девочкам быстро надоели мои заумные рассуждения и я вынужден был сменить тему. Дальше у нас сам собою возник вопрос зачем нужна математика?

Таблица интегралов 4

Перечень всех формул неопределенных интегралов (147 штук) можно найти здесь.

Представленная на этой странице таблица интегралов содержит формулы неопределенных интегралов показательных и тригонометрических функций, гиперболических и логарифмических функций. Правила решения некоторых интегралов описаны прямо в таблице. Очень часто встречается случай, когда терпение и труд всё перетрут. Монотонно применяете одну и ту же формулу до тех пор, пока применять больше нечего.

Что ещё можно сказать о некоторых неопределенных интегралах? Как видно из формул 94 и 95, тригонометрические функции синус и косинус интегрированию не подаются. При попытке их интегрирования срабатывают формулы приведения тригонометрических функций. На этом рэкетирский наезд интегралов заканчивается. А вот тангенсу и котангенсу приходится искать крышу у натуральных логарифмов. Гиперболические функции, какими бы крутыми они себя не считали, ведут себя точно так же. Кем при этом являются интегралы - представителя налоговых органов или организованной преступности? А какая разница? Результат-то для подынтегральных функций одинаковый. Вот такая вот аппроксимация интегралов на окружающую действительность у меня получилась.

И ещё один вопрос от досужего дилетанта. Я всё не мог понять, что меня смущает в соседстве обратных тригонометрических функций и логарифмических функций. Оказывается - единицы измерения. Логарифмические функции - это преобразование числа в число. Обратные тригонометрические функции - это преобразование числа в угол. У чисел и углов разные единицы измерения. Когда же мы переходим к определенным интегралам, углы обратных тригонометрических функций превращаются в единицы измерения площади. В математическом анализе принято тупо игнорировать существование единиц измерения. Не самое научное поведение. В этом плане детская арифметика (не та, которая в школе жонглирует числами, а та, которая в детском садике) на порядок выше матана - там даже складывать числа с разными единицами измерения нельзя.

Так что же такое математические функции с точки зрения банальной эрудиции? Это преобразования числовых коэффициентов при различных единицах измерения. Тогда возникает необходимость четкого разграничения тригонометрических функций и числовых последовательностей, возникающих в результате тригонометрических преобразований. Что бы не писать каждый раз "сие есть волк, а не собака". Не стоит забывать, что окружающий нас мир - это не математическая лавка, где на каждом предмете или явлении есть бирка с математической функцией.

Таблица интегралов 3

На этой странице представлена таблица интегралов, содержащих квадратное уравнение в его почти классическом виде и пузатая мелочь, состоящая из дробного отношения суммы или разности с участием неизвестного под знаком квадратного корня. Почему вид квадратного уравнения почти классический? В школе такое уравнение обычно записывают, начиная с квадрата икс, потом просто икс и заканчивают свободным членом уравнения. В интегралах почему-то такое квадратное уравнение записывается в арабском стиле. Наверное, математики, занимающиеся интегралами, и математики, занимающиеся квадратными уравнениями, исповедуют разные религии.

Больше интегралов, а именно 147 формул, можно найти здесь

Что еще примечательного в этих таблицах интегралов? В интеграле под номером 78 даны два решения, зависящие от внешних факторов (коэффициентов) уравнения. Что интересно, в одном случае в результате получается арктангенс, в другом случае - натуральный логарифм. Просматривая все таблицы логарифмов, можно заметить, что эти две математические функции идут рядом, как близнецы-братья, во многих формулах. Интересно, что именно связывает эти две функции? Ведь они живут не в одном дворе и даже не на соседних улицах. Они принадлежат разным разным разделам математики - логарифмам и тригонометрии. Или это мне так кажется?

Формулы 86 и 87 снова ставят рядом логарифмы и тригонометрию. В этот раз натуральный логарифм решил примазаться к арксинусу. Нет, между тригонометрией и логарифмами наверняка что-то есть. Может, это любовь такая математическая?

Как же интегрируются сами влюбленные? Смотрите  интегралы показательных, тригонометрических и логарифмических функций.

Тригонометрический круг синус и косинус

Тригонометрический круг представляет значения тригонометрических функций синус (sin) и косинус (cos) в виде координат точек единичной окружности при различных значениях угла альфа в градусах и радианах.

Тригонометрический круг синус и косинус

Поскольку я сам вечно путаюсь при переводе координат точек окружности в синусы и косинусы, для простоты все значения косинусов (cos) для углов от 0 до 360 градусов (от 0 пи до 2 пи) подчеркнуты зеленой черточкой. Даже при распечатке этого рисунка тригонометрического круга на черно-белом принтере все значения косинуса будут подчеркнуты, а значения синуса будут без подчеркивания. Если вам интересно, то можете посмотреть отдельные тригонометрические круги для синуса и косинуса.

Напротив указанных углов на окружности расположены точки, а в круглых скобках указаны координаты этих точек. Первой записана координата Х (косинус)

Давайте проведем обзорную экскурсию по этому уголку математического зоопарка. Прежде всего, нужно отметить, что здесь присутствует декартова система координат - одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая - вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы - cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы - sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы - на диване перед телевизором по горизонтали.

В этой системе координат нарисована окружность радиусом, равным единице. Центр окружности находится в начале системы координат - там, где в центе рисунка пересекаются оси абсцисс (ось Х) и ординат (ось У).

Из центра окружности проведены тоненькие черточки, которые показывают углы 30, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 градусов. В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.

Линии углов заканчиваются точками на единичной окружности. Возле каждой точки, в круглых скобках, записаны координаты этой точки. Первой записана координата Х, которая соответствует косинусу угла, образовавшего эту точку. Второй записана координата У этой точки, что соответствует значению синуса угла. По картинке довольно легко находить синус и косинус заданного угла и наоборот, по заданному значению синуса или косинуса, можно легко найти значение угла. Главное, не перепутать синус с косинусом.

Обращаю особое внимание на тот факт, что если вы по значению синуса или косинуса ищите угол, обязательно нужно дописывать период угла. Математики очень трепетно относятся к этому аппендициту тригонометрических функций и при его отсутствии могут влепить двойку за, казалось бы, правильный ответ. Что такое период при нахождении угла по значению тригонометрической функции? Это такая штучка, которая придумана математиками специально для того, чтобы запутываться самим и запутывать других. Особенно блондинок. Но об этом мы поговорим как-нибудь в другой раз.

Всё, что собрано в кучку на рисунке тригонометрического круга синуса и косинуса, можно внимательно рассмотреть на отдельных картинках с портретами синуса 0, 30, 45 градусов (ссылки на отдельные странички я буду добавлять по мере увеличения фотогалереи синусов и косинусов).

Найти решение:

Синусы и косинусы круг - здесь картинка во всей своей тригонометрической красе.

Угол 120 градусов в радианах - равен 2/3 пи или 2 пи деленное на 3, на картинке очень красиво нарисовано.

Значения синусов косинусов углов в радианах - на картинке есть такие, надеюсь, именно те углы, которые вы ищете.

Значение косинуса угла в 45 градусов - равно корню из двух деленному на два, можете проверить по рисунку.

Тригонометрическая окружность - я не совсем уверен, что представленная на картинке окружность является тригонометрической, но что-то от тригонометрии в этой окружности определенно есть, например, синусы и косинусы на окружности - вылитая тригонометрия.

Тригонометрический круг рисунок - есть здесь такой. Правда, не самый красивый рисунок, можно нарисовать гораздо красивее и понятнее. Мне минус в репутацию - почему я до сих пор не нарисовал его для блондинок? Представляете ситуацию в картинной галерее будущего: экскурсовод объясняет группе школьников "Перед вами всемирно известное полотно "Тригонометрическая мадонна с единичным отрезком на руках" - картина гениального художника эпохи Раннего Математического Возрождения ..." Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!

Круг синусов и косинусов - именно такой круг совершенно случайно оказался здесь на картинке.

Угол 9 градусов сколько это в пи - в пи это 1/20 или пи/20.
Решение: для перевода градусов в пи радиан, нужно имеющиеся у нас градусы разделить на 180 градусов (это 1 пи радиан). У нас получается 9/180 = 1/20

Ответ: 9 градусов = 1/20 пи.

Синус это вверх или в сторону - синус - это вверх, в сторону - это косинус.

Комментарии к этой статье запрещены. Из-за огромного их количества мои ответы на ваши вопросы о тригонометрическом круге уже не публикуются. Вопросы можете задавать в комментариях к другим страницам. Постараюсь решить проблему за счет удаления части комментариев, тем самым освобожу место для новых.

Умножение столбиком

В порядке оказания "скорой решательной помощи", сейчас мы рассмотрим одним глазом умножение столбиком. Не весь процесс целиком, а маленькие технические детали. Наши умные калькуляторы очень легко справляются с умножением разных чисел, но они не выдают распечатку умножения столбиком этих же чисел. Очень жаль. Рецепт приготовления чисел не в микроволновке (на калькуляторе), а на костре (ручками на бумажке в столбик) иногда вызывает затруднения.

Сейчас мы приготовим два блюда из чисел и умножения тем древним способом, которым пользовались наши предки в те далекие времена, когда электричества ещё не было (ведь все калькуляторы работают от электричества). Умножим столбиком две пары чисел:

0,15 * 20

120 * 60

Числа очень простые, но вот все эти нолики и запятые, как сырые дрова, мешают разгореться костру наших знаний. Для победы силы разума над древними суевериями, прежде всего, числа нужно расположить фотогенично. Не для того, чтобы сделать красивую фотку на память, а для того, чтобы нам было проще считать. Для этого хвосты из нулей в конце чисел нужно просто игнорировать. Они есть, но мы их не видим. Очки мы надели такие - противонулевые. Когда мы подобным образом разделали наши числа, можно приступать к приготовлению блюда - располагаем одно число под другим, выравнивая столбик по правому краю чисел. Нолики у наших чисел остаются (вы же не станете отрывать хвост у своего любимого домашнего животного, даже ради умножения его столбиком). Если нолики не хотят выстраиваться ровно, не обращайте на них внимания.

Умножение столбиком

В результате нам нужно умножить в столбик числа 15 на 2 и 12 на 6 (я думаю, любой уважающий себя математик с этой задачей справится). После умножения столбиком мы получим числа 30 и 72. Всё! Наше блюдо готово! Но, прежде чем подавать его на стол учителя, результат необходимо украсить нулями или запятыми. Другими словами, нужно навести порядок в нулях и запятых. Не пугайтесь! Это гораздо проще, чем наводить порядок на кухне.

Снимаем наши противонулевые очки и занимаемся нулями. Если числа при умножении в столбик мы складываем, то хвостики из нулей складывать нельзя. Их нужно просто перенести в низ и приписать к полученному результату. В первом примере у нас остался один нолик от числа 20, во втором примере у нас аж два нолика - один от числа 120, второй от числа 60. Если вам попадутся числа, у которых в конце по мешочку ноликов, то высыпайте в результат сперва один мешочек, потом второй. Смотрим, что получилось у нас:

15 * 2 = 30 плюс нолик = 300

12 * 6 = 72 плюс два нолика = 7200

Теперь берем бинокль и начинаем выискивать запятые. Во втором примере ничего похожего на запятую не наблюдается. Значит, со вторым примером мы покончили - блюдо учителю на стол! А вот в первом примере нам удалось обнаружить эту маленькую пакость. И что теперь делать? Ведь всё было так красиво... Придется эту бяку, словно пучок петрушки, воткнуть в наш результат. Иначе учитель обидится. Остается решить, куда именно втыкать. Правило очень простое - сколько знаков после запятой было до умножения, столько же знаков после запятой отделяется после умножения. Если запятые прокрались в оба числа, тогда блюдо подается с двойным гарниром - отделяется столько знаков, сколько их было в двух числах, вместе взятых. А у нас мы имеем:

0,15 - это два знака после запятой

300 минус два знака после запятой = 3,00 = 3

Всё! Задание выполнено. Можете брать в руки калькулятор и проверять. Я же, для проверки, займусь любимым делом математиков - пожонглирую числами. Следите внимательно за каждым моим движением:)

0,15 * 20 = (15 : 100) * 20 = 20 * 15 : 100 = 2 * 10 * 15 : 100 = 2 * 15 * 10 : 100 = 30 * 10 : 100 = 3 * 10 * 10 : 100 = 3 * 100 : 100 = 3 * 1 = 3

120 * 60 = 12 * 10 * 60 = 12 * 10 * 6 * 10 = 12 * 6 * 10 * 10 = (10 + 2) * 6 * 10 * 10 = (10 * 6 + 2 * 6) * 10 * 10 = (60 + 2 * 6) * 10 * 10 = (60 + 12) * 10 * 10 = (60 + 12) * 100 = 72 * 100 = 7200

Что не говорите, а математическое жонглирование - прикольная штука. Как видите, даже без калькулятора и умножения столбиком, можно довольно просто получить результат (жаль, не всегда так получается).

Таблица интегралов 2

На этой странице представлены неопределенные интегралы с квадратными корнями. Большую таблицу неопределенных интегралов можно скачать на странице таблица интегралов.

Что можно сказать о представленных здесь неопределенных интегралах и о результатах вычисления интегралов? Если предположить, что вычисление интеграла - это определенный порядок каких-то шаманских действий, известных только математикам, над математическими функциями, то некоторые функции колбасит не по детски. Например, в формулах интегралов 27 и 28 мы видим, что результат интегрирования зависит от знака постоянного члена функции. При этом логарифм при положительных значениях а с какого-то перепугу превращается в арктангенс при отрицательных значениях а. Я не хочу сказать, что математики допустили ошибку при вычислении этих интегралом, мне интересен сам факт чудесного превращения. В примерах 50 и 51 совершенно разные подинтегральные выражения дают почти одинаковый результат, отличающийся только знаком перед первым слагаемым. Вот такие вот чудеса могут происходить в математике на вполне законных основаниях.

Седьмая группа интегралов решается методом подстановки. Если вы не улавливаете смысл этой подстановки, тогда выполните действия наоборот - в результат подстановки вместо t подставьте его значение. У вас получится квадрат разности. По формуле сокращенного умножения, известной вам со школьной скамьи, раскрываете скобки. Не забывайте, что впереди стоит знак минус и знаковую ориентацию полученного многочлена нужно изменить на противоположную. В результате а в квадрате чудесным образом исчезает при вычитании себе подобного и у вас остается первоначальное выражение. Что и требовалось доказать.

Дальше нас ждут  интегралы функций, очень похожих на квадратные уравнения.