Умножение и деление на ноль

Автор Николай Хижняк

Поскольку ноль не является числом, все математические операции по умножению и делению на ноль происходят в области единиц измерения. По отношению к операции деления на ноль единицы измерения могут быть реальные и виртуальные. К реальным единицам измерения относятся единицы измерения длины. Все остальные единицы измерения, предположительно, являются виртуальными. Деление на ноль виртуальных единиц измерения невозможно, поскольку результат деления на ноль таких единиц измерения не имеет смысла.

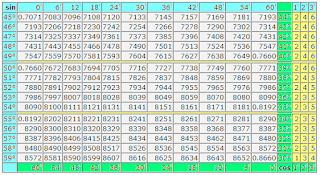
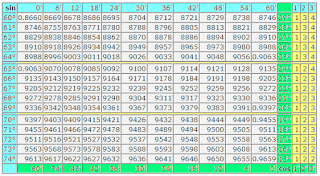
В особую группу следует выделить природную единицу измерения скоростей (скорость света) и математическую единицу измерения углов (угол в 45 градусов). Эти единицы измерения выводятся при помощи математических методов и их математические свойства требуют дальнейшего изучения. Более детального изучения требуют так же единицы измерения времени.

Виртуальные единицы измерения появляются в результате процесса, который математически можно записать как деление нуля на ноль.

0/0=1а

где а – виртуальная единица измерения.

Описанные математические свойства виртуальных единиц измерения позволяют нам вводить любые единицы измерения и пользоваться ими без влияния на окружающий мир. Эти единицы измерения применяются как для описания окружающей действительности, так и для повседневных нужд. Примерами виртуальных единиц измерения могут быть единицы измерения денег, температуры, многих физических величин или применяемые в технике и коммерции. Процесс выхода из обихода виртуальных единиц измерения можно математически отобразить как умножение на ноль. Математические свойства подобных единиц измерения проверены практикой их использования на протяжении многих тысячелетий.

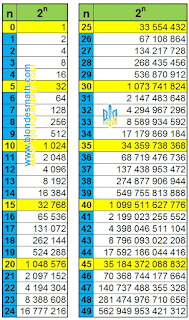
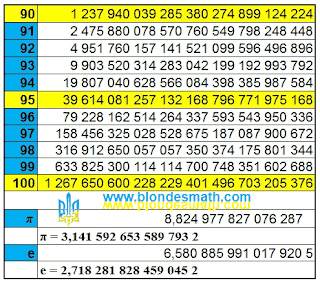
В многомерном пространстве деление на ноль увеличивает количество пространственных измерений, умножение на ноль уменьшает это количество.

В прямоугольных декартовых координатах это будет выглядеть так:

x/0 = xy
xy/0 = (x/0)y = x(y/0) = xyz

При умножении на ноль следует принимать во внимание проективные свойства пространства, поскольку результат такого умножения зависит от того, какой именно компонент умножается на ноль.

xyz*0 = 0 и xy или xz или yz
xy*0 = 0 и x или y

В физических уравнениях деление на ноль требует введения новой единицы измерения в рассматриваемое уравнением физическое взаимодействие, выражаемое математическим действием умножением (предположительно, ещё одной единицы измерения длины). Например, при делении на ноль длины получается площадь, при делении на ноль площади получается объем и так далее.

м/0 = м²
м²/0 = м³

Алгебраически это можно представить в следующем виде

a/0 = ab
ab/0 = abc

где а, b, c – взаимно перпендикулярные единицы измерения длины.

При умножении на ноль один из компонентов взаимодействия, описываемых физическим уравнением, из взаимодействия исключается. Первоначальный результат взаимодействия превращается в ноль. Оставшиеся компоненты продолжают взаимодействовать.

м³*0 = 0 и м²
м²*0 = 0 и м

Алгебраически это можно представить в следующем виде

abc*0 = 0 и ab или ac или bc
ab*0 = 0 и a или b

где а, b, c – взаимно перпендикулярные единицы измерения длины.

Пояснение для блондинок: Это только начало деления и умножения на ноль. Более детально мы во всём этом пальчиками поковыряемся и по полочкам разложим как нибудь в другой раз.

Примечание для Манула: Здесь, конечно, нет геометрии. Но мне просто лень было рисовать. Да и надоело уже всё это. Позже покажу, а сейчас есть дела поважнее:)))

Эволюция пространства

Вероятно, в процессе своей эволюции, пространство порождает различные многомерные вселенные с четным количеством измерений. Развитие происходит от пространств с меньшим количеством измерений к пространствам с большим количеством измерений. За основу существования пространства можно принять принцип существования скоростей. Наша шестимерная Вселенная в цепи эволюции пространства будет выглядеть следующим образом.

Эволюция пространства

Вполне возможно, что до Большого Взрыва, положившего начало нашей Вселенной, существовала четырехмерная вселенная, в которой энергия имела одно измерение длины, а материя два измерения длины в той части вселенной, которая соответствует нашей досветовой. В процессе эволюции этой четырехмерной вселенной образовалась черная дыра, последствием которой в шестимерном пространстве был Большой Взрыв, давший начало нашей Вселенной. Материя с двумя измерениями длины в нашей Вселенной превратилась в двухмерную энергию. Вопрос о трансформации одномерной по длине энергии в процессе перехода через черную дыру, остается открытым.

В процессе эволюции нашей Вселенной энергия с двумя измерениями длины частично переходит в материю с тремя измерениями длины. Материя порождает в нашей Вселенной черные дыры, которые дают начало новым вселенным в восьмимерном пространстве. После Большого Взрыва в восьмимерном пространстве наша материя с тремя измерениями длины превращается в энергию восьмимерной вселенной. И так далее. Процесс эволюции пространства может развиваться до бесконечности.

В ходе эволюции одна четырехмерная вселенная порождает множество шестимерных вселенных. В свою очередь каждая шестимерная вселенная порождает множество восьмимерных вселенных. Это похоже на процесс метания икры. Все шестимерные все-ленные, порождаемые одной четырехмерной вселенной, могут находиться во взаимно перпендикулярных измерениях, что исключает их взаимное влияние друг на друга. Каждая из вселенных проецируется на все другие вселенные в виде точки. Точно так же могут формироваться восьмимерные вселенные.

В отношении сверхсветовой части вселенных любого типа заслуживает внимания теория симметричности относительно скорости света. Энергия и материя досветовой части свободно перемещается в трех измерениях длины и жестко фиксирована в непрерывном потоке трех измерений времени. Темная энергия и темная материя свободно перемещаются в трех измерениях времени и жестко фиксированы в непрерывном потоке трех измерений длины. Даже если это не так, возможность существования вселенных подобного типа не стоит сбрасывать со счетов.

Процесс перехода от черной дыры к Большому Взрыву требует дополнительного изучения. Математически он может быть описан операциями умножения и деления на ноль. Есть основания полагать, что спусковым механизмом гравитационного коллапса, приводящим к появлению черной дыры, является геометрия пространства. Этот вопрос будет рассмотрен дополнительно.

Тригонометрические зависимости угла масштаба

Рассмотрим тригонометрические зависимости угла масштаба в двух прямоугольных треугольниках – при увеличении масштаба и при уменьшении масштаба.

Треугольники угла масштаба

Тригонометрические соотношения сторон полученных прямоугольных треугольников для уменьшения и увеличения масштаба сведем в таблицу.

Тригонометрические зависимости угла масштаба

Полученные результаты можно сравнить с релятивистским радикалом из теории относительности Эйнштейна.

Теория относительности Эйнштейна

Не трудно заметить, что приведенные в уравнениях радикалы очень похожи на синус и секанс уменьшения угла масштаба. Если выполнить не сложные преобразования, можно получить единицу измерения.

Математические преобразования

Проведенные преобразования указывают на то, что природной единицей измерения скоростей является скорость света. Нет никаких оснований полагать, что при прохождении через точку симметрии коэффициента масштаба происходит изменение тригонометрических зависимостей. По этому, можно предположить, что для сверхсветовых скоростей релятивистский радикал принимает следующие значения.

Теория относительности для сверхсветовых скоростей

На основании вышеизложенного можно выдвинуть следующую гипотезу о строении нашей Вселенной. Скорость сета является естественным барьером, отделяющим досветовою часть Вселенной от сверхсветовой части. Досветовую часть Вселенной мы имеем возможность наблюдать. В силу специфических свойств скорости света, сверхсветовая часть Вселенной не может наблюдаться непосредственно. Можно предположить, что скорость света является осью симметрии распределения вещества во Вселенной. Темная материя и темная энергия, которые оказывают воздействие на нашу часть Вселенной, могут находиться в сверхсветовой части Вселенной.

Если во Вселенной есть высокоразвитые разумные цивилизации, которые овладели сверхсветовыми технологиями, то для передачи информации они будут использовать не электромагнитные волны, обладающие скоростью света, а твердые носители информации на основе темной материи, передающиеся со скоростями, значительно превосходящими скорость света.

Если приравнять тригонометрические зависимости угла масштаба к значениям тригонометрических функций при 90° (это 1; 0 и 1/0), то для уменьшения масштаба они сводятся к равенству 0=1, для увеличения масштаба – к равенству k=0.

Наша Вселенная имеет три ограничения. В пространстве границей вселенной явля-ется область, где скорость света равняется нулю. Внешне наша Вселенная является точкой в пространстве. Математическим уравнением вселенной является равенство 0=1 – любая физическая величина со своей единицей измерения в масштабах Вселенной равняется нулю. Этот закон сохранения подтверждается некоторыми исследованиями физиков, в частности, об этом говорится в докладе Андрея Линде.

Кроме пространственного ограничения, существую ограничения скорости. В досветовой части Вселенной это выражается в ограничении длинны – расстояние между двумя положениями любой точки пространства во времени не может равняться нулю. В физике это ограничение принято называть абсолютным нулем температуры. Сверхсветовая часть Вселенной имеет ограничение по времени – время между двумя положениями любой точки в пространстве не может равняться нулю. Мгновенное перемещение в пространстве без перемещения во времени невозможно. Геометрически это можно выразить так: проекция скорости на длину и на время не может равняться нулю. Выполнение этих условий обеспечивается присутствием вращения на самых разных уровнях: атомарном, планетарном, галактическом. Можно предположить, что наша Вселенная так же вращается в пространстве.

Более точное представление о принципах существования Вселенной можно получить после детального изучения скорости света как физического процесса. За основу можно принять положение о том, что скорость света в нашей Вселенной является результатом взаимодействия трех измерений длинны с тремя измерениями времени. Математически это взаимодействие описывается умножением. Физически наша Вселенная имеет шесть измерений – три измерения длины и три измерения времени.

Пояснение для блондинок: Теперь самое время нарисовать нашу Вселенную и посмотреть, какое место она занимает в эволюции пространства.

Изменение угла масштаба

Увеличение угла масштаба можно представить как изменение величины при неизменной единице измерения. Уменьшение угла масштаба можно представить как изменение единицы измерения при неизменной величине. Геометрически в системе прямоугольного треугольника это будет выглядеть следующим образом.

Изменение угла масштаба

Увеличение и уменьшение масштаба в одинаковое количество раз соответствует одному значению угла масштаба. На этом свойстве углов масштаба основаны тригонометрические зависимости в прямоугольном треугольнике.

С точки зрения математического результата не имеет значения, как описывается изменение величины относительно единицы измерения. Переменная величина при постоянной единице измерения и переменная единица измерения при постоянной величине дадут одинаковое значение угла масштаба.

В общем виде изменение масштаба величины можно представить как поворот единицы измерения на величину угла масштаба. Увеличение или уменьшение масштаба зависит от того, какое положение единицы измерения принято за основу при сравнении и от вида проекции. Увеличение масштаба можно представить как лучевую проекцию на числовой луч, перпендикулярный единице измерения, взятой за основу при сравнении. Уменьшение масштаба можно представить как перпендикулярную проекцию сравниваемой единицы измерения на единицу измерения, взятую за основу.

Поворот единицы измерения

Пояснение для блондинок: Дальше заканчивается нудное вступление и начинается самое интересное - тригонометрические зависимости угла масштаба.

Таблица Брадиса синусы и косинусы

Таблица Брадиса синусы и косинусы с точностью до минуты рассчитана на блондинок. От классической таблицы Брадиса она отличается тем, что для удобства пользования этой таблицей значения углов для синусов и косинусов выделены разными цветами. Для синусов принят голубой цвет ячеек с градусами и минутами. Для косинусов принят зеленый фон ячеек. Желтым фоном выделены значения минут, которые при необходимости добавляются или вычитаются из табличных значений.

Обычно не принято так подробно подавать навигацию по таблице Брадиса. Во-первых, она рассчитана на продвинутых юзеров от математики. Во-вторых, издатели ещё с допотопных советских времен выпускают эти таблицы в черно-белом варианте и всячески экономят типографскую краску на навигации по таблице Брадиса.

Надеюсь, такое оформление не даст вам заблудиться в таблице Брадиса даже в средине этой таблицы. И вы не перепутаете синусы с косинусами при поиске их значений. Кстати, таблица Брадиса для синусов и косинусов представляет значения этих тригонометрических функций для углов от 0 до 90 градусов. Для других значений углов можете пользоваться тригонометрическим кругом в качестве шпаргалки.

Если вам нужно более точное вычисление значений тригонометрических функций, то можете воспользоваться калькулятором бесплатно онлайн прямо на этом сайте. Как пользоваться таблицей Брадиса, для тех, кто ещё не знает, мы разберемся в следующий раз.

Степени числа 2

Последовательные степени числа два

Последовательные степени числа два от 0 до 29 представлены на таблице выше. Начинается таблица степеней числа 2 с показателя степени ноль. Любое число в нулевой степени равняется единице. Поэтому два в степени 0 равняется 1. Любое число в первой степени равняется самому себе. Поэтому 2 в степени 1 равно 2.

Если кому-то мало этой таблицы, тогда можете посмотреть другую, где степени числа 2 представлены до 49-й степени.

Степени числа 2 от 0 до 49

Степени числа 2 от 50 до 69

Степени числа 2 от 70 до 89

Степени числа 2 от 90 до 100

Надеюсь, эти таблицы степеней числа 2 от 0 до 100 программистам понравятся. Математики любят совать всякую гадость куда попало. Как достойный ученик я не удержался, чтобы не всунуть в таблицу 2 в степени "пи" и 2 в степени "е". Авось, кому-нибудь из вундеркиндов это пригодится. А теперь маленький кусочек теории.

Два во второй степени означает, что число два нужно умножить само на себя. Поэтому 2 в степени 2 или 2 в квадрате равняется четырем.

2 х 2 = 4

Вообще, показатель степени показывает, сколько одинаковых чисел перемножается между собой. Так, два в третьей степени или 2 в кубе означает, что три числа 2 перемножаются между собой и это равняется восьми:

2 х 2 х 2 = 8

Два в четвертой степени будет произведением четырех двоек:

2 х 2 х 2 х 2 = 16

Эта таблица последовательных степеней числа два очень часто применяется в программировании, поскольку там используется двоичная система система счисления.

В заключение нужно ответить на вопрос вселенского масштаба: а 2 в бла-бла-бла степени на какую цифру заканчивается?

Два в любой степени заканчивается на одну из четырех цифр: 2, 4, 8, 6. Именно в такой последовательности они чередуются. (Евангелие от Меня: под выражением "любая степень" нужно понимать любое положительное целое число за исключением нуля. Аминь.) Искать формулы в Интернете мне откровенно лень. Беру карандаш и бумагу, рисую формулы - не правильно. Вторая попытка - то, что нужно. Несколько проверок - готово. Перед вами четыре формулы. Та формула, в которой при делении получается целое число, показывает, на какую цифру оканчивается два, возведенное в указанную степень.

Степени числа 2. Формулы для определения последней цифры.

На картинке приведены два примера использования формул. В первом случае 2 в степени 123456789 заканчивается на цифру 2. Во втором случае 2 в степени 11111 заканчивается на цифру 8.

Несколько ответов на вопросы в комментариях.

2 в 999 степени заканчивается на 88.

2 в 2000 и 2 в 2012 степенях заканчиваются на 6 (оба показателя степени без остатка делятся на 4).

Таблица квадратов натуральных чисел

Таблица квадратов натуральных чисел от 1 до 100

В таблице квадратов натуральных чисел представлены квадраты чисел от 1 до 100. Показатель степени числа в виде двоечки записан справа вверху того числа, которое возводится в степень. Ну, типа число-малыш залезло на плечи взрослому числу и свесило ножки. Для того, чтобы возвести в квадрат (во вторую степень) любое число, его нужно умножить на точно такое же число и записать результат.

Например, десять во второй степени равняется сто, потому что если десять умножить на десять, у нас получится сто. Пять в квадрате равняется двадцать пять, так как все знают, что пять у пять "опять двадцать пять". А вот двойка в квадрате это не что иное, как "дважды два четыре".

Квадраты чисел

Зачем математики такое придумали - степень числа? Для краткости записи математических выражений, чтобы не повторять несколько раз умножение одинаковых чисел. Если при возведении числа во вторую степень мы экономим совсем мало места, то при возведении чисел в большие степени экономия места получается довольно значительная. Наша лень - главный двигатель прогресса.

Степень числа и умножение

Особенностью квадратов чисел, как и всех остальных четных степеней числа, является то, что после возведения в степень отрицательного числа (в математике такое число уже не считается натуральным, его называют целым числом) в результате получается положительное число. Ведь минус на минус дает плюс при умножении, сколько бы раз мы этот фокус не повторяли. Отрицательное число во второй, четвертой, шестой, восьмой и так далее степенях дает в результате положительное число.

Степень отрицательного числа

Таблицу квадратов или других степеней отрицательных чисел вы врятли встретите. Это уже тот уровень математики, когда вы должны пользоваться собственными знаниями.

Обоснование теории деления на ноль

Автор Сергей Манулов

Обоснование теории делении на ноль выполняется на примере уравнения Менделеева-Клапейрона для идеальных газов.

И так уравнение Менделеева-Клапейрона (или уравнение состояния идеального газа) выглядит следующим образом:

PV=nRT (*)

где:
Р - давление (Па),
V – объём газа (м3),
R -газовая постоянная,
n –количество вещества (Моль),
Т – температура (К).

Согласно Теории деления на ноль, мы можем делить на ноль только в том случае, если за ноль принято реальное несуществующее явление - пустота. В данном случае это может быть давление, объём, количество вещества и температура. Когда одна из этих величин равняется нулю, это означает, что данное явление полностью отсутствует. Сейчас мы поэкспериментируем над ним, приравнивая параметры (P,V,n,T) к нулю, и посмотрим, что у нас будет получаться.

1) Пусть n=0. Это означает, что у нас нет вещества. Подставив это значение в уравнение Менделеева-Клапейрона (*), получаем выражение:

PV=0

Когда нет вещества, то и нет объёма. Поэтому объём будет равняться нулю. Чему же будет равняться давление? Выразим его из (*):

P=nRT\V (1)

Поскольку n=0, V=0, мы имеем неопределённость вида 0*0=0\0=ё, согласно теории деления на ноль.

Выходит, что в отсутствии материи может быть произвольное давление. Но встаёт вопрос, откуда же оно берётся? Ведь давление - это свойство материи. Но с другой стороны, невозможно измерить давление внутри пустоты, чтобы убедится, что оно действительно равно нулю. Оно может быть произвольным. Это не доказуемо и не опровержимо, на данный момент.

Только тут имеет место быть логическая ошибка. Температура - это свойство материи, в отсутствии материи мы будем иметь отсутствие температуры. Иными словами Т=0. Подставим в уравнение (1), получаем:

Р=0*R*0\0=0 (согласно теории деления на ноль)

Иными словами, давление, объём, температура не существует при отсутствии материи.

Выведем из уравнения Менделеева-Клапейрона (*) формулу расчёта газовой постоянной:

PV\(n*T)= R

Подставим в это уравнение коэффициенты P,V,n,T=0 и получим:

(0*0)\(0*0)=ё\ё=ё

Получается произвольная величина, в том числе и 8,314, что и является значением R.

2) Пусть мы имеем температуру равную 0 градусов Кельвина. Получаем следующие выражение из уравнения Менделеева-Клапейрона (*):

nRT=0
PV=0

Как известно, при нуле градусов Кельвина прекращается движение молекул и атомов, они застывают во времени, поэтому давление становится равным нулю. Нет взаимодействия, нет давления. Объём и количество вещества не будут изменяться со временем, они константа. Выведем Объём из формулы Менделеева-Клапейрон (*):

V=nRT\Р

Опять получаем неопределённость 0*0=ё. Объём может быть произволен. Остальные случаи (Р=0, V=0) взаимосвязаны со случаем 1.

Вывод: Теория деления на ноль не опровергается при эксперименте с формулой Менделеева-Клапейрона для идеальных газов.

Но стоит учесть тот фактор, что это уравнение Менделеева-Клапейрона создано для искусственной системы, которой в природе не существует. Его применяют в реальной жизни с определёнными допущениями, поэтому этот эксперимент не является реальным доказательством правоты теории деления на ноль.

Авто и эвакуатор для блондинок

Любой счастливый автовладелец, в том числе и блондинка, даже в страшном сне боится столкнуться с необходимостью вызова эвакуатора. Что такое эвакуатор? Это носилки такие специальные для вашего лимузинчика, точнее - возилки. Носить автомобильчик, даже маленький, с ресничками, тяжело. Вот и придумали их возить. Про аварии (тьфу, тьфу, тьфу!) мы говорить не будем. Но вот эти противные машины иногда ломаются. Естественно, в самый неподходящий момент. А вы вообще помните, что бы что-то нехорошее случилось у вас в подходящий момент? Лично я таких случаев не припоминаю. Так вот, любая, даже самая малюсенькая поломка автомобиля может привести к тому, что ваш шустрый и послушный автомобильчик превращается в большую кучу металлолома. Вы уже не можете доехать на нем туда, куда вам так срочно нужно.

Авто и эвакуатор для блондинок

Вот в подобных ситуациях нужно вызывать эвакуатор. Сразу возле вас он не появится, его нужно будет ждать. Всё зависит от того, в какой именно точке вашего маршрута вас настиг злой и коварный рок. А это может быть где угодно - у автомобильчиков нет специальных мест для поломок, у автомобильчиков есть только специальные места для стоянок. Ваш вредный автомобиль может сломаться за городом в таком месте, из которого к ближайшей галактике добраться гораздо проще, чем к родной цивилизации.

Или наоборот, вы сломались в самом центре цивилизации, но противные злые силы все подъезды к вам позатыкали непроходимыми автомобильными пробочками, через которые эвакуатору ну никак не пробраться. Так что вам придется ждать.

Это мы рассмотрели одну проблему при поломке вашего чудного автомобильчика. Но мы совсем не сказали о другой проблеме. А кого и как, собственно, звать на помощь? Кричать "Ау! Хелп ми плиз!!!" бесполезно. Эвакуатор - это точно такая же железяка, как и ваша. Она английского не понимает. Впрочем, как и русского. Для таких ситуаций нужно знать номер телефона того, кто скажет дядьке в эвакуаторе, что бы он ехал к вам. Поэтому, если сами ездите на своем лимузинчике, поройтесь в интернете и запишите в свой мобильный телефон слово "Эвакуатор" и рядом номер телефона. Так, на всякий случай.

Но и это еще не всё! Теперь самая большая проблема - ориентация в пространстве. Прежде, чем набирать записанный в телефоне номер, вам нужно понять, в каком именно месте и на какой именно дороге сломалось ваша любимая машинка. Ведь тот дядька или тетка, который возьмут трубку, должны будут объяснить тому дядьке, который в эвакуаторе, где именно вас искать. Вспомните, откуда и куда вы ехали. Что интересного вы уже проехали, а что проехать ещё не успели. Если рядом есть домики, то на них должны быть таблички с буковками - это название улицы. Циферки на этой же табличке обозначают не математику, а номер дома. Вот их и нужно прочитать в телефон. Если вы стоите среди поля или леса (ой, кошмар!), то нужно вспомнить, как все называют то последнее место, которое вы только что проехали. И как все называют то место, до которого вы доехать не успели. Запомните, что ни дядьки, ни тетки не знают, в каком магазине вы были в прошлую пятницу или куда на выходных вы ездили с подругой.

Ну, и последнее. Если вы совершенно случайно в этот злополучный день забыли дома свой телефон, не отчаивайтесь. У вас есть огромное преимущество перед мужчинками - вы блондинка! А какой мужчина откажется помочь блондинке в беде? На картинке ниже показано, какого результата от них вам нужно добиться.

Авто и эвакуатор для блондинок

Нерешаемые уравнения в детском садике

Решение нерешаемого уравнения вызвало некоторые вопросы. Сейчас мы с другой стороны посмотрим на нерешаемое уравнение номер 1:

x + 2 = x

Для этого мы создадим специальную исследовательскую группу и проследим за её поведением, при условии, что будут "воспроизведены обстоятельства, в которых условия задачи соблюдаются". В исследовательскую группу мы включим:

1) Ребенок из детского садика. Он только начинает постигать азы математики но уже весьма сообразителен.
2) Блондинка, мама ребенка из детского садика. Когда-то в школе учила математику и знала её довольно неплохо. Сейчас напрочь всё забыла за ненадобностью.
3) Профессор математики Де Кольте. Блестяще владеет математическим аппаратом, решает самые сложные математические задачи.
4) Николай Хижняк. Инженер, увлекается математикой, утверждает, что понимает эту абстрактную науку.

Вы скажете, что это не честно, включать себя в состав исследовательской группы. Но, уважаемые, я эту группу придумал, я предлагаю кандидатов в её состав, я утверждаю окончательный состав исследовательской группы. Это самый демократический принцип. Я честно воспользовался демократическим правом быть избранным и победил в конкурсе кандидатов :)))

И так, попросим нашу исследовательскую группу решить простую задачку и дать алгебраический вариант её решения:

У нас есть неизвестное количество ежей к которому прибавили двух ужей. Сколько ежей получилось?

В результате исследовательская группа выдала следующие решения.

1) Ребенок из детского садика. Как я уже говорил, ребенок довольно смышленый и умеет решать логические задачки, в которых нужно угадать ход мыслей автора задачи и дать такой же ответ, который ждет от ребенка автор задачи. Это такой метод дрессировки будущих зомби, которые хорошо умеют угадывать то, что ждут от них хозяева. Ребенок ответил "Получится неизвестное количество ёжиков". На просьбу записать решение этой задачки на листике бумаги, ребенок ответил, что писать он ещё не умеет, но может нарисовать ёжика.

2) Блондинка, мама ребенка из детского садика. На словах задачку решила правильно после целого ряда наводящих вопросов. На просьбу записать свое решение при помощи алгебры, соскребла из глубин памяти все остатки математических знаний и начала рассуждать следующим образом: "Так, алгебра, алгебра... Ниии-чё не помню... Значит алгебра - это неизвестное... Вау! Обозначим неизвестное количество ежиков через "х". Количество ужиков нам известно и его обозначать не нужно, просто циферку запишем... Прибавление у нас - это значок "плюс". Вот!". Блондинка протягивает лист бумаги, на котором записано:

x + 2 = x

3) Профессор математики Де Кольте. На просьбу решить подобную задачу про ежей и ужей знаменитый профессор возмутился, что, дескать, не подобает великому ученому решать такие детские задачи и отправил нас за решением в детский сад. На нашу просьбу записать алгебраическое решение этой задачи, профессор непонимающе уставился на нас, долго думал и сказал: "Хорошо, я подумаю над этой проблемой". А дальше было следующее...

Для алгебраического отображения решения данной задачи профессор разработал специальную теорию треугольных интегралов, за которую он был удостоен звания "академик". Треугольному интегралу было присвоено имя автора и он стал называться "треугольный интеграл Де Кольте"...

Для решения этой конкретной задачи был создан специальный исследовательский институт во главе с теперь уже академиком Де Кольте. После нескольких лет напряженной работы, на свет появился многотомный научный труд под названием "Практическое применение треугольного интеграла Де Кольте в пределах по радиусу выреза на платье"...

Весь этот околонаучный бред мы изучать не будем. Нас интересует только результат. Открываем сразу последнюю страницу последнего тома. Там перечень каких-то организаций... Листаем страницы к началу книги в поисках ответа на задачу... Где-то в средине последнего тома находим строчку "Данная работа выполнена в счет отработки научных грантов: ...". Ого! Эта свора проходимцев от науки на ровном месте умудрилась сожрать целую кучу денег! А перед этой строчкой можно найти и ответ на нашу задачу. Там написано "х" с целой кучей оговорок.

4) Николай Хижняк. Этот знахарь математики глубокомысленно выдал страницу под названием "Решение нерешаемых уравнений". По его мнению, существует и другая задача, в которой спрашивается, сколько ежей получится, если к двум ежам прибавить неизвестное количество ужей. Он уверяет, что обе задачи имеют одинаковое решение :)))

Кстати, есть ещё одна интересная задача про ужей и ежей:

Смесь ужа и ежа - это метр колючей проволоки. Как математически записать это выражение?

Нерешаемые уравнения в детском садике

Треугольный интеграл Де Кольте по вырезу платья не применять :)))

Блондинки и математика

На тему математики и блондинок рассуждает Сергей Манулов. В авторской редакции статья называется

Гомо Бланди-матхикус

Наш мир построен на борьбе двух основополагающих принципов – разрушения и созидания, являющихся противоположностью друг к другу. Эти принципы имеют огромное множество форм на всех уровнях бытья: физическом, духовном и ментальном. На каждом из этих уровней, имеются свои подуровни, на них свои и так бесконечности. Все они имеют в себе свойства этих двух основополагающих принципов.

Например, если рассматривать микромир, то принципы могут быть выражены в виде двух антиподов - катионов и анионов. В среднем мире – кислоты и щёлочи. В макромире –материя и антиматерия.

В ментальном мире: логика и иррациональность.

В духовном мире: добро и зло, свет и тьма, хорошо и плохо.

Блондинки и математика

Хаос и порядок относится ко всем уровням и подуровням.

У всего есть антипод. Это аксиома, без доказательства. Но теперь встаёт вопрос, что есть разрушение, а есть созидание? Бывает же, что чтобы создать что-то, нужно разрушить. А иногда создавая что-то, разрушаешь другое. Всё относительно и зависит от точки отсчёта нуля. Он символизирует чашу весов в нейтральном, уравновешенном положении. И если допустить, что когда весы сдвинуты вправо – это созидание, а влево это разрушение, тогда и можно будет понять, что есть что. Но почему вправо это именно созидание, а влево разрушение? Потому, что мы так допустили. Но ведь можно посмотреть и наоборот? И тогда принципы поменяют свои места. Но тогда весы бессмысленны? Да именно так. Поскольку разрушения и созидание неразделимы. Разрушение это форма созидания, созидание – форма разрушения. У них одна природа, как у катионов и анионов, у материи и антиматерии. Всё едино. Более того, всё состоит из одного принципа, который в зависимости от количественности, принимает различные качества. Мир един, нужно это признать.

Но давайте уйдём от глубоких философских абстракций и придём, к чему-нибудь земному, и на примере этого разберёмся со смыслом слов произнесённых выше.

В качестве подопытных кроликов возьмем людей, с особым логическим складом мышления – математиков, не использующих иррационализм. В противовес к ним в качестве антипода подберём блондинку, существо, лишённое логики, зато иррационализма, хоть отбавляй.
И так, математик не любит блондинку за её интеллект. Блондинка же не понимает математиков и считает его занудой. Между ними интеллектуальная пропасть. Им не найти общего языка. Почему они столь разные? Вроде бы один вид – Гомо Сапианс, то бишь человек разумный, а вот ведут себя по отношению друг к другу неразумно. Причина тому кроется в развитии этих двух индивидуумов.

Математиками не рождаются ими становятся, в отличии от блондинок. Что же, верно, но части. Но ведь и не все блондинки натуральные, не все ими родились, ими потом стали, покрасившись. Так значит, работает и обратная логика – математиками рождаются. А всё потому, что люди все разные. Различимее между ними пропасть, если смотреть совокупность всех их черт. Каждый рождается с определённой предрасположенностью – одни имеют рациональный склад ума, другие иррациональный. Одни гуманитарии другие технари. Математик у нас это учёный(!) технарь, доведённый до абсолюта. Блондинка же гуманитарий, даже похуже, необразованный гуманитарий! Как рождается учённый? В муках учения, он забивает себе голову логикой точных наук, построенной другими учёнными. В результате его разум становится точным и рациональным, особенно если он родился с таким менталитетом. А необразованная блондинка, просто выросла, впитала минимум информации, и живёт себе довольная.

И вот встретилась эта парочка и давай изъяснятся друг с другом. Математик говорит, применяя огромное количество терминов и слишком заумные лексические конструкции, а блондинка несёт что-то невразумительное, не точное, абстрактное. Не удивительно, что им вместе не ужиться. Но зато у каждого из них есть свои плюсы. Математик может доказать что угодно используя свою логику, а блондинка выдумать что угодно. Вот только минусов тоже хватает: математик не признаёт то что выходит за рамки уже построенной логики, а блондинка не может обосновать логично выдуманное. Из-за этого страдает наука. Математики не могу принести что-то принципиально новое из-за самоограничения. Блондинки же не могут донести это новое. Что же делать? Выращивать новый вид человека: Хомо Блондматхкиус (Homo Blondmathicus), то есть Человек Матиматиково-блондинистый, собирающий в себе лучшие черты обоих вида. Золотая середина, умеющая отвергать старое, на более новое лучшее и обосновывать его. Такой человек может всё.

Но что делать уже существующим – математику и блондинке? Я советую блондинкам учить математику и другие науки, развивать свой кругозор, незатуманленое детское мышление. А математикам забыть все аксиомы, забыть истины. И попытаться их открыть вновь. И понять, что они всё-таки открыли.

Что такое абсолютная истина?

Автор этой статьи - Сергей Манулов.

Главная проблема любой логики - узкая её направленность и принятие любых произвольных аксиом. Софизм. Возможность доказать что угодно построением логических цепей. При этом логика будет идеально выдержана и нельзя подкопаться. Но, тем не менее, она может быть и ошибочной.

Что-то чем больше я думаю о нуле, тем больше мне кажется, что вся наука которая сейчас ВЫДУМАНА, человеками-учёными является софизмом. Где-то работающим, где-то нет. Но зато, работает главное студенческое правило - если что-то не выходит, подгоняй! И они подгоняют, вполне успешно. Я заметил, что и я выкручиваюсь со своею теорией. Сначала я говорил, что она работает на всю математику, затем я её ограничил до абстрактной математики. Если найдут ещё один аргумент, я найду ещё контраргумент. Ооох это всё бессмысленно, но и смысл в этом есть.

Люди имеют великий дар - мыслить, но это и великое проклятие. Особенно, когда понимаешь обе точки зрения, а середину между ними не видишь. На распутье. Абсолютная истина заключается в том, что нет абсолютной истины. И вот тут уже возникает парадокс, если нету абсолютной истины, то откуда вытекает эта абсолютная истинна про отсутствие абсолютной истинны? В этом и есть весь смысл, в отсутствии смысла, что в свою очередь тоже парадокс. А всё почему? А всё потому что люди ограничивают себя логикой, а она не может быть абсолютной, никогда. Любая логика это лишь выдумка, хорошая софистская выдумка, ничего более.

Давайте обратимся к книге книг.

Вначале было слово.

«Вначале было слово…» - так начинается первая строка книги Нового Завета Евангелие от Иоанна. Что есть слово? Давайте-ка копнём вглубь. Слово есть способ озвучивания мысли. Мысль порождает слово, слова мысль. Слово и мысль неотделимы друг от друга. Они едины. Но связано мышление лишь только со словами? Нет. Мы можем мыслить без использования слов – образами и чувствами. Более того, я утверждаю, что образное мышление является более мощным, чем словесное. Сейчас я это докажу.

Как известно, слова это набор образов и чувств, позволяющий нам упростить и ускорить процесс мышления. Например, вместо того чтобы приводить следующие описание: шар, покрытый рыжей коркой, имеющий кисло-сладкий запах и вкус, мы просто говорим апельсин. И в тот же миг, мы понимает, что оно означает. Если хорошо развито воображение и память, даже можем его представить. Вот в чём прелесть слов.

Согласитесь, использовать слово намного проще, чем воображать все компоненты образующий образ апельсина в голове (корка, запах, вкус и так далее). Каждое слово, обязательно связано хотя бы с одним образом. Но, не все образы связаны со словами. Некоторые образы можно чувствовать, видеть, понимать, но вы не можете сразу подобрать для них конкретное слово, поскольку они только что появились в этом мире в результате вашего мыслительного процесса. Поэтому вам приходится придумывать для них новое слово, а так же попытаться как можно точнее описать их старыми словами. В этом главный недостаток словесного мышления.

Люди, которые не мыслят образами, имеют меньше шансов придумать новые образы, то есть придумать что-то новое. Таких людей называют шаблонно мыслящими. Ведь слово – это шаблон. Мыслить образами намного труднее, чем словами. Для этого нужно особый склад ума. Некоторые люди от рожденья имеют такой дар, другим же придётся его развивать.

Теперь замените слово на логику и поймёте о чём я сейчас говорю. Логика это уже зафиксированные слова, она не вносит ничего нового, логика строится с самоограничения. А при самоограничении невозможно ощутить всё таинство вселенной, поскольку имеется парадокс знания: «Чем больше я знаю - тем меньше не знаю».

Но и один иррационализм не выход. Можно такого себе по навыдумывать, что попросту будет бредом сивой кобылы. Истина найдётся только при уравновешенном использовании логики и иррационализма. Золотая середина применима ко всему, что делает человек.

Вывод: абсолютная истина – это истина по середине двух противоборствующих сторон, то есть усредненный результат совокупности всех точек зрения. Но даже это является лишь абстрактной моделью, но она будет наиболее близка к истине. Потому что истина это совокупность всего.

Другие работы Сергея Манулова:
Теория деления на ноль
Что есть ноль?