Внешние углы треугольника

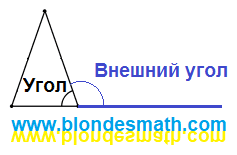
Внешний угол треугольника

Вот такая вот просьба: Здравствуйте! Помогите пожалуйста. Определите, является ли треугольник АВС тупоугольным, если два его внешних угла равны 135 и 160 градусов.

Понятие внешних углов в треугольнике - это тот мусор, который уже давно пора выбросить из математики. Спросите у любой блондинки, она когда-нибудь одевает свое платье наизнанку? Она его всегда носит так, как положено. А вот математики углы в треугольниках меряют и так, и сяк. Получается, блондинки умнее математиков - они умеют правильно пользоваться вещами.

Передо мной нет школьного учебника и я не знаю, как правильно нужно решать эту задачу. Можно решить двумя способами - на лицо и на изнанку. Начнем с того, что по уверениям математиков, сумма внешнего и внутреннего углов в любой вершине треугольника равна 180 градусов. Картинку я здесь рисовать не буду, она есть на другой странице - нечего распространять заразу невежества, даже если оно математическое.

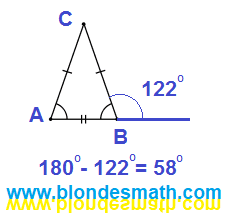
Для нормального решения нужно от внешних углов треугольника перейти к внутренним и найти величину третьего угла. Считаем:

180 - 135 = 45 градусов
180 - 160 = 20 градусов

И так, у нас есть два угла треугольника. Является ли он тупоугольным? Судя по этим двум углам - нет. Напоминаю, что тупоугольным называется треугольник, у которого один угол тупой. Тупой не в смысле умственных способностей, а в смысле количества градусов. Если угол перебрал больше 90 градусов, то его принято считать тупым. Ой! Опять что-то не то. Ну, короче, вы поняли. Кто не понял - открываем учебник и зубрим тупой угол.

Так вот, два угла у нас острых. А третий? Вот тут нам на помощь приходит теорема (или как там её математики называют) о сумме углов треугольника. Как бы это не называлось, но сумма углов любого треугольника всегда равна 180 градусов. Напоминаю, свое платье мы одеваем сейчас нормально, поэтому речь здесь идет о внутренних углах треугольника. Зная величину двух углов, найти третий - задачка для малявок.

180 - 45 - 20 = 115 градусов

Треугольник у нас тупоугольный, поскольку третий угол больше 90 градусов и является тупым. Не по жизни тупым, а просто тупым, как отдельные представители отдельных наук.

Теперь решаем эту же задачу, только наизнанку. Пусть блондинки посмеются над такими математиками, как мы. И так, сумма внешнего и внутреннего углов в каждой вершине треугольника равна 180 градусов. Сколько у нас вершин? Правильно - три. Треугольник всё-таки, не хухры-мухры. Считаем, чему равна сумма внешних и внутренних углов? Три вершины по 180 градусов... Итого:

3*180 = 540 градусов

Если калькулятор нам не врет. Выше мы уже говорили, что сумма внутренних углов треугольника равна 180 градусов. Отнимаем её от общей суммы:

540 - 180 = 360 градусов

Получается, что сумма внешних углов треугольника равна 360 градусов. Ведь только она у нас и осталась, внутренние углы из суммы мы уже выбросили. Любой шустрый математик в подобных случаях громогласно заявляет: "Теорему о сумме внешних углов треугольника можно считать доказанной!".

Теперь вывернем наизнанку тупоугольный треугольник и посмотрим, как должен выглядеть он. Если один внутренний угол у него должен быть больше 90 градусов, значит этот же внешний угол должен быть меньше 90 градусов. Давайте считать по внешним углам:

360 - 135 - 160 = 65 градусов

Калькулятор утверждает, что даже наизнанку наш треугольника всё равно тупоугольный. Не знаю, как вам, а мне математика наизнанку совсем не нравится. В приличном обществе это моветон, всё равно что одежду наизнанку носить.

P.S. Кстати, математики даже понятие внутреннего угла наизнанку толком вывернуть не могут. Если рассуждать "интуитивно понятно", то внешний угол - это то, что мы можем измерить снаружи, то есть 360 градусов минус внутренний угол. Как меряют талию у блондинок? Становятся перед нею и вытянутыми вперед руками пытаются что-то там сделать.

Что это было?

Математика Евромайдана

Математика Евромайдана

При помощи математики можно описать всё, что угодно. Было бы желание. Ведь математика - это то, что происходит в окружающем нас мире. Вот посмотрите, какой бардак творится в Украине:

3-7y-3(2-3y) = 4(y-1)-(y+1)

Знак равенства - это баррикада на Майдане. Числа - это люди без масок, игреки - это люди в масках. Скобки - это щиты, за которыми прячутся и те, и другие. Кто скрывается под масками? Вот вопрос, на который мы должны дать ответ. А под масками прячутся все: и друзья, и враги. В математике есть очень хороший способ отличать своих от чужих - это знаки плюс и минус. Всех своих врагов мы помечаем знаком минус, всех друзей - знаком плюс. Кому какие знаки присваивать? Это зависит от того, по кукую сторону баррикады мы сами стоим. Ведь в этом мире всё относительно.

Для того, чтобы увидеть лица под масками, сначала нужно избавиться от щитов скобок. Достаем волшебную палочку и убираем все щиты.

3-7y-3(2-3y) = 4(y-1)-(y+1)
3-7y-6+9y = 4y-4-y-1

Теперь лица в масках загоняем по одну сторону баррикад, лица без масок - по другую. В международной практике это принято делать дубинками, в быту - палками. Не забываем, что перебежчики через баррикаду меняют сою знаковую принадлежность. Это по ту сторону баррикады они были врагами и им цепляли ярлык "минус". Здесь они уже друзья и имеют знак "плюс". К сожалению, с врагами происходит то же самое - там они были друзьями со знаком "плюс", у нас они превращаются во врагов со знаком "минус".

3-7y-6+9y = 4y-4-y-1
-7y+9y-4у+у = -4-1-3+6

Теперь начинается кровавая бойня на украинском Майдане. Те, кто имеет знак "минус", уничтожают тех, кто имеет знак "плюс". При этом сами погибают смертью героев. Но это с точки зрения наших врагов. Мы же в подобных случаях говорим: "Туда им и дорога". По другую сторону баррикад рассуждают точно так же. К сожалению, в жизни всё не так, как в математике - жертва умирает, а убийца продолжает жить. Здесь действует совсем другой математический закон: сквозь прицел снайперской винтовки все мы выглядим одинаково - просто мишени.

-7y+9y-4у+у = -4-1-3+6
9у+у-7у-4у = 6-4-3-1
-у = -2

Сказки обычно имеют счастливый конец. В этом конкретном примере результат получился отрицательным, как это нередко случается в жизни. Естественно, каким бы уродом не являлся победитель, он себя считает хорошим. В человеческой истории не принято судить победителей. Поскольку победило зло, переходим на сторону победителя. При этом меняем знаки и зло превращается в добро:

-у = -2
у = 2

Как видим, под маской скрывалось обычное лицо. И добро, и зло всегда скрываются под масками человеческих лиц.


Памяти Небесной Сотни посвящается.


P.S. Вы не представляете, какое это счастье - решать те математические задачи, которые хочется решать, а не те, которые решать заставляют. Наверное, это можно сравнить с пением любимых песен, а не тех, которые петь заставляют.

Один из гимнов киевского Евромайдана, песню группы Океан Ельзи "Я не здамся без бою" ("Я не сдамся без боя"), поют грузинские артисты и их показывают по телевизору на всю страну. Называется эта страна Грузия.

Артисты из Латвии поют гимн Украины и их показывают по национальному телевидению.

Россияне, а вы когда-нибудь видели по телевизору своих артистов, на концерте поющих гимн Америки?

Умные люди ищут себе друзей, а дураки - врагов. Не ищите дураков, они вас сами найдут.

Площадь поверхности параллелепипеда

Площадь поверхности параллелепипеда

Очередная задача про прямоугольный параллелепипед. Точнее, про площадь поверхности параллелепипеда. Почему мне так нравятся именно прямоугольные параллелепипеды? Во-первых, решение задач у них проще, чем у косоугольных параллелепипедов, призм, цилиндров и прочей геометрической мути. Во-вторых, прямоугольный параллелепипед - это среда нашего обитания. Среда не в смысле вторник, четверг, а в смысле джунглей для обезьян. Мы обитаем внутри таких параллелепипедов. Если верить заверениям наших доблестных строителей, они прямоугольные. Во всяком случае, к этому стремятся. Прямоугольная комната - это и есть прямоугольный параллелепипед. Кирпич или коробка для обуви - это тоже он, родимый.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 9 и 24. Диагональ параллелепипеда равна 41. Найдите площадь поверхности параллелепипеда.

Вот о чем поведала нам задача. Да, это не любовный роман. К тому же, уже прочитанный. Зная две стороны и диагональ прямоугольного параллелепипеда, третью сторону можно найти по старой доброй формуле дедушки Пифагора. Такую задачу мы совсем недавно рассматривали. Я не буду заморачиваться с картинками, а расскажу на пальцах.

Возводим диагональ в квадрат и вычитаем сперва квадрат одной стороны, затем квадрат другой стороны.

41*41 - 9*9 - 24*24 = 1681 - 81 - 576 = 1024

Это мы получили квадрат третьей стороны. После этого извлекаем квадратный корень и получаем третью сторону длиной 32. Кого-чего? А какая разница? К числам можно любую единицу измерения прилепить. Главное - без фанатизма. Если вы будете измерять прямоугольный параллелепипед долларами или градусами Цельсия, то вас никто не поймет. По умолчанию предполагается, что в нашем случае возле чисел должны стоять единицы измерения длины: метры, сантиметры, дюймы, локти...

Теперь переходим к площади поверхности прямоугольного параллелепипеда. В комнате это площадь четырех стен, пола и потолка. Все они из себя представляют прямоугольники. Тупо умножаем размеры прямоугольников и получаем их площади. У нас должны получиться три пары площадей - передняя и задняя стенки, левая и правая стенки, пол и потолок. Записываем формулу площади поверхности параллелепипеда и считаем:

S = 2(a*b + b*c + a*c) = 2(9*24 + 24*32 + 9*32) = 2(216 + 768 + 288) = 2*1272 = 2544

Вот и всё. Площадь поверхности параллелепипеда оказалась равной 2544 единицы измерения площади.

Внешний угол при вершине треугольника

Очередная задача про равнобедренный треугольник:

В треугольнике АВС АС=ВС. Внешний угол при вершине В равен 122 градуса. Найдите угол. Ответ дайте в градусах. Можно мне все подробно?

Постараюсь объяснить как можно подробнее. Почему я сразу сказал, что задача про равнобедренный треугольник? У обычных треугольников все стороны разной длинны. Их даже так и называют - разносторонние. Берем картинку со страницы про виды треугольников, отрезаем ненужное и начинаем разукрашивать. Геометрия - это та же детская разукрашка, только проще. В задаче обычно всегда говорится, что именно и как вы должны разукрашивать. Разукрасим нашу картинку с видами треугольников по размерам сторон синенькими буквами вершин равнобедренного треугольника.

Виды треугольников

Теперь нужно разобраться, что такое внешний угол при вершине треугольника. По моему глубокому убеждению, это мусор, которым математики засоряют вам мозги. Ведь чем больше всякого мусора в учебнике, тем больше часов нужно на его изучение и тем больше сможет заработать учитель. Чем запутаннее предмет, тем легче репетиторам найти работу. Это похоже на продажу овощей на вес - чем больше в них грязи, тем больше денег заработает продавец.

И так, открываем "умную" книжку и начинаем копаться в математической грязи. В книжке написано буквально следующее:

Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.

По умолчанию предполагается, что мы уже должны знать, что такое смежный угол. Не знаю, как вы, а я уже давно забыл, что это за фигня такая - "смежный угол". Ведь все нормальные люди пользуются нормальными углами. Хорошо, что к определению внешнего угла треугольника картинка прилагается, которая проясняет, как именно он выглядит.

Внешний угол

Я никогда не пойму, зачем к треугольнику лепить внешний угол, если у него уже есть обычные, внутренние, углы. Я так понимаю, что одни дураки когда-то учили других, а те тупо повторяют действия учителей. Своими мозгами пользоваться их так никто и не научил. Кстати, величайшим достижением современного образования можно считать отсутствие в учебной программе научной теории о трех китах и Земле, которая на них держится. И это только потому, что данная теория не относится к математике. А ведь если в учебной программе что-то записано, то учить это обязательно для получения хорошей оценки.

Ладно, по возмущался и хватит. Вернемся к наше задаче. Читаем внимательно: Внешний угол при вершине В равен 122 градуса. Собственно, картинка внешнего угла - это то, что доктор прописал. Обычный угол треугольника получается путем вычитания из 180 градусов внешнего угла. У равнобедренного треугольника углы при основании равны. Рисуем картинку и сразу решение.

Внешний угол при вершине

Кажется, я догадываюсь, откуда в математике могли появиться внешние углы. Когда европейцы увидели пирамиды древнего Египта, они были потрясены увиденным. Им захотелось измерить эти грандиозные сооружения. Вот только внутренний угол пирамиды измерить не представляется возможным. Можно измерить внешний угол и высчитать внутренний. Математики увидели, что делают другие, и записали в свою Математическую Библию определение внешнего угла треугольника. Вот с тех пор это Священное Писание переписывается из учебника в учебник.

Сравни, поставь знак больше, меньше или равно

Знаки больше и меньше

Задача на единицы измерения и сравнение чисел с разными единицами измерения. Звучит она так:

Сравни. Поставь знак больше, меньше или равно.
80 см2 ... 8 дм2
236 см2 ... 2 дм2
40 дм2 ... 4000 см2
754 дм2 ... 7540 см2
15000 см2 ... 15 дм2
25600 см2 ... 256 дм2

Здесь сравниваются единицы измерения площадей, точнее сантиметры квадратные и дециметры квадратные. Для сравнения двух разных величин, их нужно привести к одной единице измерения. К какой именно? Не имеет значения. Главное, чтобы и возле одного числа, и возле другого числа единицы измерения были одинаковы.

Для перехода от одной единицы измерения к другой, необходимо выполнить определенные вычисления. Как учат нас математики? Точно не помню, но, кажется, они пользуются таблицами перевода одних единиц измерения в другие. Для нужных нам сантиметров квадратных и дециметров квадратных выглядит это так:

1 см² = 0,01 дм²
1 дм² = 100 см²

Теперь берем одно наше значение, применяем к нему переводной коэффициент и можем смело сравнивать с другим значением.

80 см² = 80*0,01 дм² = 0,8 дм² меньше 8 дм²
236 см² = 236*0,01 дм² = 2,36 дм² больше 2 дм²
40 дм² = 40*100 см² = 4000 см² равно 4000 см²
754 дм² = 754*100 см² = 75400 см² больше 7540 см²
15000 см² = 15000*0,01 дм² = 150 дм² больше 15 дм²
25600 см² = 25600*0,01 дм² = 256 дм² равно 256 дм²

Как выглядят знаки больше и меньше можно посмотреть на отдельной странице. Со знаком равно всё гораздо проще - две палочки "Твикс". А вот как запомнить знаки больше и меньше смотрите по ссылке. Один из способов.

Корни квадратные, корни благородные

Упрощение выражений в математике бывает разное. Вот пример выражения, в котором фигурируют корни квадратные, корни благородные. Почему эти корни благородные? Они без всяких прибамбасов и наворотов, скромненькие такие.

Корни квадратные, корни благородные

Упрощение дробного выражения с квадратными корнями не такое страшное, как может показаться. Не нужно сразу вдаваться во все подробности и в уже прятаться под кровать. Прищурьте один глаз и посмотрите на выражение издалека. Ну, дробь. Ну, две дроби. Нужно их сложить. Как складываются дроби? Вспоминаем далекое детство и правило сложения дробей. Чтобы сложить две дроби, нужно их привести к общему знаменателю. После этого два числителя складываются и остаются под одним общим знаменателем.

После этой детской процедуры, которая даже в высшей математике выполняется точно так же, у нас получились фрагменты выражения, которые очень смутно напоминают о формулах сокращенного умножения. Открываем формулы, открываем второй глаз и смотрим в оба.

Вау! Да ведь это же они, родимые, и есть! Квадрат разности, квадрат суммы, разность квадратов даже чья-то добрая душа уже на сомножители разложила. Что делать теперь? Вместо одной половинки формулы нужно записать в наше выражение вторую половинку. Но вот разность квадратов уже записана в виде второй половинки формулы. Ни-фи-га! Возвращаем всё на Родину! В знаменателе записываем разность квадратов в первозданном виде. Это математики нас специально запутывают, чтобы посмеяться над нами, когда мы из калькулятора начнем корни выковыривать.

Посмотрите, как всё чудненько получается! Все наши квадратные корни возводятся в квадрат и волшебным образом исчезают. А те, что возводиться не хотят, скромненько вычитаются и превращаются в ноль. В результате упрощения такого страшного дробного выражения у нас получилась детская дробь с самыми обычными числами. Складываем числа в кучку, сокращаем дробь и получаем результат без всякого калькулятора. Собственно, для этого упрощение выражений и применяется.

Формулы сокращенного умножения

Страничка моего любимого справочника по математике, на которой увековечены формулы сокращенного умножения. Весьма полезная штучка, довольно часто приходилось заглядывать. Не смотря на заголовок, я что-то в упор не вижу формул сокращенного деления. Как видите, даже в справочниках бывают ошибки и опечатки. Нельзя слепо верить книжкам, как бы они не назывались.

Формулы сокращенного умножения

Здесь и сами формулы сокращенного умножения, и их названия. И так, на картинке у нас представлены: квадрат суммы, квадрат разности, куб суммы, куб разности, разность квадратов, сумма и разность кубов, сумма и разность четвертых степеней, произведение двучленов, преобразование произведения и другие обитатели математического зоопарка.

Очень примечательна формула преобразования произведения в сумму и разность. Оба элемента возводятся в квадрат. А возведение в квадрат - это то же умножение. Это мы друг другу можем сколько угодно рассказывать, что умножение - это многократное сложение. Математику не так-то просто обмануть.

Очень поражает странность математиков. Как когда-то какой-то церковно-приходской дьячок нацарапал гусиным пером формулы сокращенного умножения для квадрата суммы и квадрата разности, так их из учебника в учебник и переписывают. Абсолютное отсутствие мозгов и воображения. Даже в школе никто из математиков никогда не учился. Или это им в институте мозги матаном убивают? Любой школьник знает, что от перестановки местами слагаемых сумма не меняется. Я вот о чем.

Квадрат суммы и квадрат разности

Не знаю, как вас, а меня простота и красота такой математики покорила раз и навсегда. Не надо забывать, что вся современная математика проходит мимо жизни. Это древние математики научили нас измерять расстояния, время и углы. Они научили нас складывать и умножать. Что прижилось от современной математики? Проценты. Тупые бюрократы считают процент отката, обыватели изучают проценты по кредитам, бизнесмены дрожат над процентами прибыли. Вот такая она, современная математика жадных мародеров.

Кстати, вопрос для любознательных блондинок. Смотрим на предпоследнюю формулу возведения в квадрат трех слагаемых. Теперь вопрос. Если возвести в квадрат четыре слагаемых, то в результате получим сумму квадратов четырех слагаемых плюс удвоенные произведения... Сколько элементов ещё нужно прибавить? Работают ли правила комбинаторики? Я ответ не знаю. Честно.

Прямоугольный параллелепипед и диагональ

Очередная задача про прямоугольный параллелепипед и диагональ. Звучит задача так:

Дано abcda1b1c1d1 - прямоугольный параллелепипед. dd1cc1 - квадрат. dc = 3, bd1 = корень из 22. Найти bc. Доказать, что bcd1 и dc1b1 взаимно перпендикулярны.

Здесь важны два момента:

1. Правильно нарисовать картинку и разобраться, что дано, а что нужно найти.
2. Подобрать нужную формулу для решения.

Начнем с картинки. В условии сказано, что одна из граней - квадрат. Чем знаменит квадрат? У него все стороны имеют одинаковую длину. Так что фактически нам известны две стороны прямоугольного параллелепипеда и диагональ. Нужно найти длину третьей стороны.

Прямоугольный параллелепипед и диагональ

Так, что-то квадрат на картинке у меня совсем не получился, но ведь и я не Малевич. Какая картинка под рукой была, ту и разукрасил. Корень квадратный возле диагонали корявый какой-то вышел. Но оно и понятно - сейчас зима, у нас корни не растут. В супермаркет завезли корни из Австралии (там сейчас лето), вон он какой зеленый, не дозрел ещё. Потому и корявый.

Для решения задачи применяем старую добрую теорему дедушки Пифагора для прямоугольного параллелепипеда. Тысячи лет люди нею уже пользуются и останется она неизменной на все оставшиеся времена. Если я, конечно, более общий вид её здесь не опубликую. Но это как-нибудь в другой раз.

Гласит теорема Пифагора следующее: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов измерений (или сторон) параллелепипеда. Какие измерения есть у прямоугольного параллелепипеда? Их три: длина, ширина, высота. Возводим их в квадрат, складываем в кучку, выковыриваем из суммы квадратный корень и получаем длину диагонали. Очень простенький рецепт.

В нашей задаче известны диагональ и две стороны. Найти нужно третью сторону. Жонглируем формулой и находим выражения для определения третьей стороны. Подставляем значения и задача решена.

Теперь о доказательстве. С детства ненавижу доказательства. Доказывать другим, что я не дурак? Глупо. Насколько я понимаю, в данном случае от вас требуется продемонстрировать свои знания признаков перпендикулярности плоскостей. Есть у меня умная книжка по математике и там написано буквально следующее:

Признак перпендикулярности плоскостей.

Теорема 1 (о перпендикулярности). Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Перпендикулярные плоскости

Снова вспоминаем, что я не Малевич. Откуда мы знаем, что указанные плоскости проходят через перпендикулярные прямые? А дядька или тетка в условии задачи написали, что передняя и задняя грани нашего прямоугольного параллелепипеда являются квадратами. А как известно всем, диагонали у квадрата перпендикулярны. В детском садике так учили. Ну, или в школе.

Сторона равнобедренного треугольника

Вот крик о помощи, в котором просят помочь найти сторону равнобедренного треугольника:

Помогите, пожалуйста! Я не понимаю геометрию(( У меня задача по типу вот этой, только числа другие. Мне бы сам ход решения.

ЗАДАЧА: Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Найдите боковую сторону треугольника, если его площадь равна 25.

Помочь мне не трудно, но есть одна проблема: я понятия не имею о школьной программе и не представляю, что можно использовать при решении задачи, а что нельзя. Если просто брать математику и использовать её для решения, то задача решается довольно просто.

Начинаем рассуждать. У нас есть площадь равнобедренного треугольника и угол при его вершине. Нужно найти длину боковой стороны. Можно использовать теорему Пифагора, тригонометрические функции и всё то, чему вас учили до этого момента. Используя разные трюки с подстановками, можно в конце концов найти решение этой задачи. Я поступлю гораздо проще.

Для определения площади треугольника существует много разных формул. Вот к ним-то я и предлагаю присмотреться внимательнее.

Площадь треугольника формулы

Все эти формулы есть в Википедии, можно их отыскать и в разных математических справочниках. Шестая формула нам подходит как нельзя кстати. Здесь площадь треугольника определяется по боковой стороне и углам. Зная площадь треугольника, можно легко найти сторону. Осталось только с углами разобраться. Углы в основании равнобедренного треугольника равны. На картинке запишем те условия, которые превращают обычный треугольник в равнобедренный.

Равнобедренный треугольник

Как видите, нам даже нет необходимости искать углы в основании равнобедренного треугольника - синусы этих углов равны и сокращаются в дроби. Угол в вершине равен 30 градусов, синус этого угла равен одной второй. Теперь легко можно решить задачу. Выражаем квадрат стороны через площадь и синус угла в вершине, извлекаем квадратный корень и получаем сторону размером в 10 единиц.

Это взрослое решение. Все взрослые пользуются справочниками, не вдаваясь в подробности. Для инквизиторов от математики такое решение может показаться богохульством. Специально для инквизиторов мы сейчас выведем формулу площади равнобедренного треугольника через боковую сторону и синус угла в вершине. Как и предыдущее решение, это будет пример того, как нужно пользоваться математикой.

Стоп! Я обещал писать в режиме реального времени. Так вот, всё, что написано до сих пор, писалось в ночь с пятницы на субботу. Сейчас утро воскресенья. Почему я сразу всё не написал? Ну, во-первых, у меня проблемы с картинками тригонометрических формул - программа, в которой я их писал, начала глючить и не переключается на английский язык. Во-вторых, я, наверное, чувствовал, что у этой задачи есть очень простое, детское, решение. Сегодня утром до меня дошло.

Почему-то все самые интересные решения ко мне приходят по утрам. Может, я ночью с инопланетянами общаюсь? Может, это они за меня задачки решают? Есть там у них какой-то канал, типа Ютуба, под названием "Из жизни идиотов". Когда им становится грустно, они включают этот канал и начинают ухохатываться над нашими математиками с их идиотскими определениями и не менее грамотными решениями. Потом появляюсь я со своим; "Не могу решить задачу...". Они долго смеются и один говорит другому: "Покажи этому дурачку картинку, пусть исчезнет с экрана". Формулы можно записывать разными загогулинами и вкладывать в эти загогулины разный смысл. А вот геометрия на всю вселенную одна и у инопланетян равнобедренный треугольник выглядит точно так же, как и у нас. Именно поэтому инопланетяне понимают, что делают наши математики и им становится очень смешно. Мы ведь тоже смеемся, наблюдая за некоторыми проделками животных.

Это было маленькое лирическое отступление. Теперь перейдем к инквизиторским пыткам и я на время превращусь в математика-садиста, который будет мучить вас тригонометрией. Для начала картинка нашего равнобедренного треугольника с сохранением всех обозначений, принятых для произвольного треугольника. Почему я об этом специально говорю? Из-за тупости отдельных наших математиков. Если в формуле треугольника фигурирует один угол, то математик обозначит его как "альфа" и ему по барабану, этот угол находится в основании или в вершине треугольника. Это уже потом он будет тыкать пальцем в картинку и рассказывать, что именно этот угол он имел в виду, а не какой-нибудь другой. Когда же посторонний человек попробует воспользоваться такой формулой, вот тут и начинаются все проблемы в математике. И так, картинка.

Равнобедренный треугольник

Теперь тригонометрические пляски с бубном.

Вывод формулы площади равнобедренного треугольника

Краткое пояснение к этой шаманской пляске. Площадь треугольника равна половине произведения основания на высоту. Высоту и основание выражаем через боковую сторону и тригонометрические функции угла при основании треугольника. Дальше переходим к углу в вершине треугольника, точнее, его половине. На следующем этапе используем тригонометрическую формулу произведения синуса и косинуса, но с учетом того, что у нас одинаковые углы. Потом всё складываем в кучку и получаем искомую формулу площади равнобедренного треугольника.

Но всё гениальное просто. Давайте разрежем наш равнобедренный треугольник пополам и сложим две половинки в прямоугольник.

Равнобедренный треугольник и прямоугольник

А как известно, площадь любого четырехугольника равна половине произведения его диагоналей на синус угла между ними. Наша боковая сторона равнобедренного треугольника превратилась в диагональ прямоугольника, угол в вершине равен углу между диагоналями. Мы получаем ту же формулу площади равнобедренного треугольника.

Ну и наконец, само решение задачи.

Сторона равнобедренного треугольника

Картинки получились плохими. Но мы это как-нибудь переживем. Главное - их смысл.

Решение системы уравнений

Решение системы уравнений

Сегодня мы будем решать систему двух уравнений с двумя неизвестными. Выглядит эта система вот так:

x - y = -2
xy - y = 10

Благодаря усилиям многих поколений математиков это увлекательное занятие превратилось в очень нудную процедуру. С таким же успехом и теми же методами церковно-приходские дьячки вдалбливали "Слово Божье". Меня же здесь заинтересовал один момент - насколько правильная та математика, которую нам проповедуют в школе? Ответ я ещё не знаю и пишу эту статью в режиме реального времени. В настоящей математике результат не может зависеть от способа решения. Посмотрим, что получится у нас.

И так, решение системы уравнений мы будем производить способом подстановки. Самый популярный способ в истории человечества. Когда правители направляют свои войска на врагов - это и есть способ подстановки. Сами правители под стрелы и пули не лезут,они подставляют других. Поиск козла отпущения - это ещё одна разновидность способа подстановки, когда ищут того, кто ответит за чужие грехи. Но вернемся к решению нашей системы уравнений.

Говорят, что все изобретения сделаны лентяями ради облегчения собственной жизни. Способы решения, которым нас учат математики - из той же оперы. Давайте проанализируем наши уравнения и попытаемся сделать некоторые выводы. В первом уравнении у нас есть икс без всяких прибамбасов и игрек с прибамбасом в виде знака минус перед ним. Во втором уравнении икс умножается на игрек и присутствует игрек со знаком минус.

Для решения системы уравнений методом подстановки нужно одну неизвестную выразить через другую. Что через что выражать? Для получения результата это не имеет никакого значения. А вот для количества потраченных усилий в ходе решения разница есть. Произведение икса на игрек во втором уравнении сразу должно вас насторожить. Почему? Здесь неизбежно возникнут дроби. А возиться с дробями - удовольствие ниже среднего. Вот смотрите чему будет равен икс:

xy - y = 10

ху = 10 + у

х = (10 + у)/у

Теперь посмотрим, чему получится равным игрек:

xy - y = 10

у(х - 1) = 10

у = 10/(х - 1)

Такое только в страшном сне может присниться. А ведь эти дроби ещё нужно вставить в первое уравнение и найти значение неизвестной. Мрак.

Смотрим на первое уравнение. Здесь картина гораздо приятнее. Смотрим, как будет выглядеть икс:

x - y = -2

х = у - 2

Даже у игрека прибамбас в виде знака минус исчезает при телепортации его в другую часть уравнения, за знак равенства. Теперь найдем игрек:

x - y = -2

-у = -х - 2

у = х + 2

Полученные из первого уравнения выражения для икса и игрека выглядят очень гламурненько и не идут ни в какое сравнение с дробями, полученными из второго уравнения.  Мудрый вывод может быть только один - нужно из первого уравнения найти выражение для любой неизвестной и подставить его во второе уравнение.

Какое неизвестное лучше подставлять во второе уравнение? Здесь нужно пользоваться правилом лентяя - чем меньше раз будем подставлять, тем лучше. Во втором уравнении икс представлен в единственном экземпляре и подставлять придется только один раз. А вот игреков у нас аж два. Следовательно, подставлять придется тоже аж два раза.

Вот мы и получили принцип решения заданной нам системы уравнений методом подстановки: из первого уравнения находим икс и подставляем значение икса во второе уравнение. Смотрим, что у нас получилось:

xy - y = 10

(у - 2)*у - у = 10

у² - 2у - у = 10

у² - 3у = 10

у² - 3у - 10 = 0

Как видите, у нас получилось квадратное уравнение. С детства не люблю квадратные уравнения, а слово "дискриминант" на меня вселенскую тоску находит. К счастью, времена церковно-приходских решений миновали и у нас появилась замечательная возможность воспользоваться специальной программой для решения квадратных уравнений. Вводим в ячейки значения наших коэффициентов 1; -3; -10 и получаем два значения игрека:

у = 5

у = -2

Подставляем эти значения в первое уравнение и получаем значения иксов:

х = у - 2 = 5 - 2 = 3


х = у - 2 = -2 - 2 = -4

В результате решения системы уравнений с двумя неизвестными ми получили две пары значений икса и игрека:

х = 3; у = 5

х = -4; у = -2

Прежде, чем делать глубоко научные выводы, нужно выполнить проверку. Подставляем каждую неразлучную пару в наши уравнения и смотрим результат. Первая пара пошла на проверку:

х - у = 3 - 5 = -2

ху - у = 3*5 - 5 = 15 - 5 = 10

За ней отправляем другую пару:

х - у = -4 -(2) = -4 + 2 = -2

ху - у = (-4)*(-2) -(-2) = 8 + 2 = 10

Всё чудненько сходится, значит систему уравнений мы решили правильно. Вот теперь и наступил момент познания истины - сейчас мы изменим ход решения системы уравнений.  Из первого уравнения найдем игрек и подставим значение игрека во второе уравнение. Вот как это выглядит:

у = х + 2

ху - у = 10

х(х + 2) - (х + 2) = 10

х² + 2х - х - 2 = 10

х² + х - 12 = 0

У нас получилось квадратное уравнение с другими коэффициентами: 1; 1; -12. Вставляем их в дырочки и получаем два значения иксов:

х = 3

х = -4

Теперь находим два значения игреков:

у = х + 2 = 3 + 2 = 5

у = х + 2 = -4 + 2 = -2

Как видим, другой ход решения дает точно такой же результат. Вывод может быть только один - математики научились правильно решать системы уравнений. Чему и нас учат. А вот зачем нам это нужно - это уже совсем другой вопрос. Ответ "Все так учились" в современном мире уже не катит, нужны аргументы боле весомые. Разумные существа всегда понимают, что именно и для чего они делают. Дрессированные животные просто повторяют то, чему их научили.