Арктангенс на калькуляторе

Как всегда, самое интересное происходит в комментариях. Вот один из последних:

Извините за беспокойство.
Для супруги тут понадобилась тригонометрия, для юридического(!) института (маленький курс информатики - раздел "работа с калькулятором"). С синусами и косинусами я (завязавший с алгеброй 10 лет назад) кое-как разобрался.
В ступор вводит "элементарный" вопрос...
Есть tg3х=4, надо вычислить угол "х"...
Не знаю с какой стороны подойти...
Разъясните... Спасибо.

Этого зверя приручают через обратные тригонометрические функции. В нашем случае нужно использовать арктангенс. Выглядит это приблизительно вот так:

tg3х=4
arctg(tg3х)=arctg4

Дальше довольно просто (объясняю для юридического))))))) - арктангенс тангенса равен просто углу, в данном случае 3х. Это типа украсть и положить обратно))) Дословный перевод с бытовухи на язык тригонометрии будет звучать приблизительно так:

"Украли угол 3х" - tg3x;
"Украли и положили на место угол 3х" - arctg(tg3x).

Теперь совсем детский вопрос: "Что у на лежит на месте?". Правильно, угол 3х. С левой частью мы разобрались.

Рассмотрим правую часть. Тупые менты обнаружили у скупщика краденного число 4. Из оперативных данных известно, что перекупщик сдал краденный угол по курсу тангенса. Вопрос не для тупых ментов: "Какой угол был украден, если скупщик краденного по курсу тангенса получил за него число 4?". Для ответа на этот вопрос мы можем использовать таблицу значений тангенса в качестве прейскуранта обмена углов на числа среди скупщиков краденного. Но у нас тупо задана тема "работа с калькулятором". Значит мы обязаны пользоваться не бумажной таблицей (в век планшетов смешно звучит), а пластмассовым калькулятором.

Как найти арктангенс на калькуляторе? Я воспользуюсь тем, что у меня всегда под рукой. В калькуляторе "Виндовс" вводим число 4, затем нажимаем кнопочку "Inv".

Арктангенс на калькуляторе. Шаг 1.

При этом внимательно следим за кнопочкой "tan". На этой кнопочке должна появиться степень минус единичка. Четверка должна оставаться неизменной.

Арктангенс на калькуляторе. Шаг 2.

Вот теперь нажимаем кнопочку тангенса в минус первой степени и получаем значение угла, тангенс которого равен 4. Если у нас на калькуляторе включен пыптик "Градусы", то получим 75,963756532073521417107679840837 градусов.

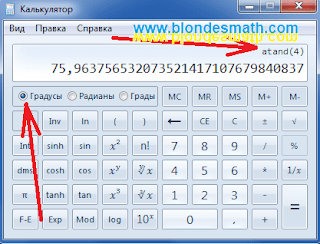Арктангенс на калькуляторе. Шаг 3.

Если на калькуляторе включен пыптик "Радианы", получим 1,3258176636680324650592392104285 радиан.

Арктангенс в радианах

Вот теперь мы можем восстановить картину до совершения преступления (в градусах и радианах картины маслом выглядят по-разному). Запишем с самого начала в градусах, округлив до трех знаков:

tg3х=4
arctg(tg3х)=arctg4
3х=75,964
х=75,964/3
х=25,321 (градуса)

То же самое, но теперь в радианах:

tg3х=4
arctg(tg3х)=arctg4
3х=1,326
х=1,326/3
х=0,442 (радиан)

Если у вас в руках калькулятор какой-либо другой конструкции, то вам нужно методом научного тыка выковырять из калькулятора нужный результат)))

Справедливости ради нужно отметить, что инквизиторы от математики могут потребовать учесть в ответе периодичность тригонометрической функции тангенс. В этом случае к полученному ответу добавляем маразм в виде "плюс пи эн" (для радиан) или "плюс 180 эн". Специально для особо ортодоксальных математиков можно указать, что эн равно нулю, плюс-минус единице, плюс-минус два и так далее до скончания века, пардон, чисел.

Ну, и особенно меня порадовал ответ на мои объяснения.

...Огромная вам благодарность за это математическое расследование...
Ваше объяснение настолько вдохновило, что на этой волне мы с супругой решили все «задачи с калькулятором». Ещё раз спасибо!
P.S. Почитал ваш профиль в гугле. И скажу, что ещё как гражданин России, разделяю ваши взгляды на террористические Донецк и Луганск. Желаю сил вам и украинскому народу додавить террористов и потихоньку возвращать себе К.R.Ы.М. Мы верим в Украину без кRемлR! Успехов вам!

Я тоже верю, что донецких и луганских террористов мы замочим даже в кремлевском сортире, что российская армия уберется с Украины, что путин перестанет совать свое свиное рыло в чужие дела и что Крым снова будет Украиной.

Сумма всех ребер параллелепипеда

Вот такая вот задача у нас имеется:

Сумма всех ребер параллелепипеда ABCDA1B1C1D1 равна 120 см. Найдите длины ребер, если AB:BC:AA1=4:5:6.

Для начала, посмотрим, что это за зверь такой - параллелепипед и где именно у него расположены ребра.

Сумма всех ребер параллелепипеда

Этот зверек из геометрического зоопарка хоть и кривоват слегка, но всё равно симпатичный. А имеется у него три группы ребер, по четыре ребра одинаковой длины в каждой группе. Сумма длин всех этих ребер по своему смыслу является периметром параллелепипеда. По аналогии с периметром четырехугольников. Ну, да ладно, не нам математиков учить.

Решить эту задачу можно при помощи пропорций, выражая одну сторону через другую. Вот пример решения задачи про сумму всех ребер параллелепипеда, где через икс обозначена одна из сторон.

Сумма всех ребер параллелепипеда решение

Отношения сторон в этом варианте задачи выражены двумя пропорциями. За икс принята самая длинная сторона, чтобы дроби в решении получались правильные, то есть меньше единицы.

Но есть и более простое решение. Я бы назвал его "метод произвольных единиц измерения". Думаю, такого в учебнике вы не найдете. В чем смысл метода произвольных единиц измерения? Для начала давайте посмотрим, как появилась подобная задача.

Кто-то измерил длины трех разных граней параллелепипеда и высчитал по формуле сумму всех ребер. Дальше, от нечего делать, он начал смотреть на соотношение длин сторон этого параллелепипеда. Будучи фанатиком математики, этот кто-то взял и тупо сократил дроби. При этом сократились не только числа, но сантиметры. Вместо размеров параллелепипеда в сантиметрах у нас остались только числа 4; 5; 6. Да, это пропорции сторон параллелепипеда, которые останутся неизменными, в каких бы единицах измерения мы этого зверя не измеряли: в сантиметрах, в метрах, в дюймах, в попугаях или мартышках. Кстати, очень поучительный мультфильм о единицах измерения длины, называется "38 попугаев".

Вот и у нас получается, что заданные в пропорциях размеры параллелепипеда не понятно в чем измерялись. Если эту неизвестную единицу измерения мы обозначим через икс, то мы легко можем подсчитать сумму всех ребер параллелепипеда, только выраженную в иксах:

4(4х+5х+6х)=4*15х=60х

У нас периметр получился равным 60 непонятных (или произвольных) единиц измерения. По условию задачи известно, что этот же периметр равен 120 сантиметров. Составляем уравнение и находим величину произвольной единицы измерения. Это просто, как в первом классе.

60х=120см
х=(120/60)см
х=2см

Теперь остается только пересчитать размеры параллелепипеда в сантиметрах.

a=4х=4*2см=8см
b=5х=5*2см=10см
c=6х=6*2см=12см

Вот еще подобная задача:

Измерения прямоугольного параллелепипеда относиться как 9:13:7. Найдите сумму ребер прямоугольного параллелепипеда, если длина меньшей стороны 18 см.

Обозначаем через икс произвольную единицу измерения и находим сумму ребер прямоугольного параллелепипеда

Р=4(9х+13х+7х)=4*29х=116х

Длина наименьшей стороны нам известна и в произвольных единицах измерения, и в сантиметрах. Отсюда найдем величину произвольной единицы измерения.

7х=18см
х=(18/7)см

Теперь мы можем определить сумму ребер.

Р=116х=116*(18/7)см=(2088/7)см

Когда можно применять метод произвольных единиц измерения? Когда нам заданы размеры какой-либо геометрической фигуры в виде пропорции сторон и что-нибудь ещё (одни сторона, периметр, площадь или объем) в человеческих единицах измерения (сантиметрах, метрах или попугаях))).