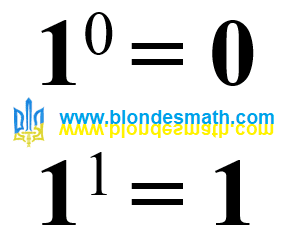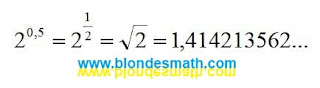Числовые спирали и простые числа

Числовые спирали и простые числа

https://doi.org/10.5281/zenodo.15024975

Начало: Числовые спирали введение

Все простые числа вида Р находятся в начале числовых лучей на всех числовых спиралях, за исключением простого числа а, расположенного на главной оси а-спирали. Взаимное расположение простых чисел будет меняться в зависимости от числа а, которое лежит в основе построения спирали. Расположение простых чисел на разных числовых спиралях показано на рисунках ниже.

Простые числа на 2-спирали

Простые числа на 3-спирали

Простые числа на 4-спирали

Простые числа на 5-спирали

Составные числа находятся на лучах спиралей, построенных на числах, являющихся делителями этих чисел. На остальных спиралях они расположены в начале числовых лучей. Например, число 6 находится на продолжении 3-луча 2-спирали и является результатом умножения числа 3 на число 2. Это же число 6 находится на продолжении 2-луча 3-спирали и является результатом умножения числа 2 на число 3.

Рассмотрение числовых спиралей будет продолжено в последующих публикациях.

Числовые спирали и системы счисления

Числовые спирали и системы счисления

https://doi.org/10.5281/zenodo.15024975

Начало: Числовые спирали введение

Числа на числовых спиралях могут быть представлены в разных системах счисления. Для примера рассмотрим числа на главной оси некоторых спиралей в разных системах счисления. Таблица 1 показывает числа на главной оси 2-спирали в двоичной, десятичной и шестнадцатеричной системах счисления.

Главная ось 2-спирали

В таблице 2 представлены числа на главной оси 10-спирали в тех же системах счисления.

Главная ось 10-спирали

Аналогично, в таблице 3 представлены числа на главной оси 16-спирали.

Главная ось 16-спирали

Как видно из таблиц выше, каждая а-спираль в системе счисления с основанием а будет состоять из отдельных витков с числами, имеющими одинаковое количество разрядов в позиционной системе счисления. Каждый следующий виток числовой спирали для числа а в системе счисления с основанием а добавляет один разряд в позиционной системе записи чисел. Каждый n-виток состоит из чисел, записываемых при помощи n+1 количества разрядов.

Если ввести правило, что единичные дуги на одном витке должны быть одинаковой длины, тогда числовая спираль превратится в набор концентрических окружностей. Каждая окружность будет содержать числа с одинаковым количеством разрядов. Введение подобного правила нарушает визуальную непрерывность натуральных чисел.

Таким образом, каждая а-спираль является графическим отображением натуральных чисел в системе счисления с основанием а, которая записана в выбранной нами системе счисления. По умолчанию мы применяем десятичную систему счисления.

Продолжение: Числовые спирали и простые числа.

Анализ числовых спиралей

Анализ числовых спиралей

https://doi.org/10.5281/zenodo.15024975

Начало: Числовые спирали введение

Движение вдоль витков любой а-спирали является таблицей сложения с последовательным добавлением одной единицы к предыдущему числу, начиная с единицы. Движение вдоль лучей любой а-спирали является таблицей умножения с последовательным умножением числа, расположенного в начале луча, на число а. Эти два движения перпендикулярны, что свидетельствует о принципиальном различии сложения и умножения.

Если провести ось симметрии через главную ось любой а-спирали, тогда симметричные числа на витках образуют суммы разложения. Для любого a.n-витка эта сумма разложения равна aⁿ+aⁿ⁺¹. Для примера суммы разложения показаны на 4.1-витке. Количество таких сумм, учитывая сумму чисел aⁿ и aⁿ⁺¹ на главной оси, равно m_n/2.

Суммы разложения

Данное свойство числовых спиралей позволяет вычислить сумму натуральных чисел, расположенных на одном а.n-витке. Для этого необходимо сумму разложения умножить на количество таких сумм, используя формулу (1), добавить число, расположенное на оси симметрии, которое равно половине суммы разложения и вычесть число aⁿ⁺¹, которое относится к следующему витку:

Сумма чисел на витке

Формула (3) позволяет вывести уже давно известную формулу для определения суммы всех натуральных чисел от единицы до любого числа а. Для этого необходимо определить сумму чисел на нулевом витке а-спирали и добавить само число а:

Сумма натуральных чисел

Если построить числовую спираль для бесконечно большого числа (∞-спираль), начало этой спирали будет отличаться от числового луча только отсутствием нуля. Нулевой виток будет состоять из бесконечно большого количества единичных дуг, каждая единичная дуга будет ограничена лучами с бесконечно малым значением угла. Кривизна витка станет проявляться в районе очень больших чисел от начала спирали.

Продолжение: Числовые спирали и системы счисления.

Описание числовых спиралей

Описание числовых спиралей

https://doi.org/10.5281/zenodo.15024975

Начало: Числовые спирали введение

2-спираль

2-спираль

На 2-спирали главная ось образуется последовательными степенями числа 2. Все нечетные числа располагаются в начале числовых N-лучей, все четные числа расположены на N-лучах спирали.

На 2.0-витке находится одна единичная дуга размером 360°, в начале этого витка находится число 1. Это единственная числовая спираль, у которой на нулевом витке нет других чисел, кроме единицы. Количество чисел и единичных дуг определяется по формуле (2).

2.1-виток разбивается на две единичные дуги размером 180° и на нем расположено два числа – 2 и 3. Здесь и на остальных витках количество чисел и единичных дуг определяется по формуле (1).

Вычисления для 2-спирали

2.2-виток образуют четыре единичные дуги размером 90°, на котором располагаются числа 4, 5, 6, 7. Число 6 расположено на продолжении 3-луча.

2.3-виток образуют 8 единичных дуг размером 45°. На этом витке распложены числа с 8 по 15 включительно. Числа 10, 12 и 14 расположены на продолжении 5-луча, 3-луча и 7-луча соответственно.

Дальнейшее расположение натуральных чисел на 2-спирали можно проследить на рисунке выше.

3-спираль

3-спираль

Главную ось 3-спирали образуют последовательные степени числа 3. На 3.0-витке находится две единичные дуги размером 180° и на нем расположено два числа – это 1 и 2. Количество единичных дуг и чисел определяется по формуле (2).

3.1-виток разбивается на шесть единичных дуг размером 60°, на нем располагаются числа 3, 4, 5, 6, 7 и 8. Количество единичных дуг и чисел определяется по формуле (1). Число 6 находится на продолжении 2-луча и является результатом умножения числа 2 на число 3.

Вычисления для 3-спирали

3.2-виток образуют восемнадцать единичных дуг размером 20°, на нем располагаются числа с 9 по 26.

4-спираль

4-спираль

Главную ось 4-спирали образуют последовательные степени числа 4. На 4.0-витке находится три единичные дуги размером 120° и на нем расположено три числа – 1, 2 и 3.

4.1-виток разбивается на двенадцать единичных дуг размером 30°.

Вычисления для 4-спирали

4.2-виток разбивается на сорок восемь единичных дуг размером 7,5°.

Каждый виток 4-спирали содержит в себе два сжатых витка 2-спирали. Сжатие происходит неравномерно и задается структурой нулевого витка 4-спирали. Нулевой и четные витки 2-спирали сжимаются до 1/3 витка 4-спирали, первый и нечетные витки – до 2/3. Такое неравномерное сжатие обеспечивает равенство единичных угловых сегментов всех витков в структуре 4-спирали.

Подобное неравномерное сжатие происходит и на остальных спиралях, построенных на числах, равных степени числа а, больше первой степени. Так, для 8-спирали (а=2³), каждый виток которой содержит три витка 2-спирали, пропорции равны: 1/7, 2/7, 4/7.

5-спираль

5-спираль

Главную ось 5-спирали образуют последовательные степени числа 5. На 5.0-витке находится четыре единичные дуги размером 90° и на нем расположено четыре числа – 1, 2, 3 и 4.

5.1-виток разбивается на двадцать единичных дуг размером 18°.

Вычисления для 5-спирали

5.2-виток разбивается на сто единичных дуг размером 3,6°.

Подобным образом можно построить числовую спираль для любого натурального числа.

Продолжение: Анализ числовых спиралей.

Числовые спирали

Числовые спирали

https://doi.org/10.5281/zenodo.15024975

Начало: Числовые спирали введение

Если для визуального отображения натуральных чисел использовать произвольную спираль и единицы измерения углов, тогда все числа можно упорядочить по следующим правилам:

1. На главной оси а-спирали располагаются числа вида aⁿ в порядке возрастания, где а>1, n≥0.

2. Главная ось совпадает с нулевым лучом единиц измерения углов и имеет следующий вид:

Главная ось числовой спирали

3. Главная ось делит спираль на отдельные витки размером в 360°, которые целесообразно нумеровать по показателю степени числа а, расположенного в начале каждого витка. Например, а.0-виток, а.1-виток, а.n-виток. Расстояние между витками спирали произвольное.

4. Каждый виток а-спирали разбивается лучами на равное количество единичных угловых секторов, которые делят виток на единичные дуги. Каждая единичная дуга имеет произвольную длину и соответствует одной числовой единице. Единичные дуги разделяют два соседних натуральных числа, которые располагаются на пересечениях лучей и витков спирали.

5. Количество единичных секторов и количество натуральных чисел m_n для каждого а.n-витка определяется по формуле (1).

6. Для нулевых витков всех а-спиралей количество единичных секторов и натуральных чисел определяется по формуле (2).

Формулы числовых спиралей

7. Каждая единичная дуга из витка m_n на следующем витке m_n+1 делится на а единичных дуг новыми лучами.

8. В начале каждого луча (N-луч), на пересечении с витком, расположено натуральное число N вида P_a, простое по отношению к числу а.

9. На продолжении N-лучей, в точках пересечения с последующими витками, располагаются натуральные числа, кратные числу а, образующему главную ось а-спирали.

Продолжение: Описание числовых спиралей.

Числовые спирали введение

Числовые спирали

https://doi.org/10.5281/zenodo.15024975

Аннотация

Числовые спирали – это представление натуральных чисел на спирали в единицах измерения углов. Соблюдение определенных правил размещения чисел позволяет получить бесконечную спиральную таблицу умножения для любого натурального числа а>1. Внешний вид и структура конкретной а-спирали будут одинаковыми для любых единиц измерения углов в любых системах счисления натуральных чисел.

Введение

Визуальное изображение натуральных чисел известно давно и имеет вид числового луча.

Числовой луч

Для визуализации чисел на числовом луче используются единицы измерения длины. Числовой луч начинается с нуля, поскольку иначе невозможно изобразить единичный отрезок как единицу измерения. Расстояния между числами одинаковые и равны единичному отрезку.

В 1963 году Станислав Улам предложил изображение натуральных чисел в виде спирали. Сегодня это визуальное представление натуральных чисел известно как скатерть (или спираль) Улама.

Скатерть Улама

Двумерная плоскость разбита на квадраты одинакового размера. В центре спирали находится единица, вокруг неё в каждый квадрат вписывается одно натуральное число по спирали. Данная спираль построена без применения каких-либо единиц измерения, ноль отсутствует.

В 1994 году Роберт Сакс расположил натуральные числа по Архимедовой спирали и получил спираль, известную сегодня как спираль Сакса (в Википедии описана в разделе "Вариации скатерти Улама").

Спираль Сакса

Для построения спирали Сакс использовал единицы измерения углов для поворота и единицы измерения длины для определения расстояния от центра спирали до каждого натурального числа. В центре спирали расположен ноль единиц измерения длины, на нулевом луче единиц измерения углов Сакс расположил квадраты натуральных чисел.

Продолжение: Числовые спирали.

1 в степени 0

Раньше я никогда не обращал внимания на странное равенство – 1 в степени 0 равно 1 в степени 1. Любое число в степени 0 равно единице. Любое число в первой степени равно такому же числу. Если число равно единице, получается интересное равенство.

1 в степени 0

В процессе изучения теории чисел я дошёл до того места, где общепринятый вариант возведения единицы в нулевую степень нарушает логику определённых правил. Логически правильный результат получается, если единица в нулевой степени равна нулю.

1 в степени 0, 1 в степени 1

Введение одного условия в общие правила привело к изменению многих очевидных утверждений, которые без этого условия не вызывали бы никаких сомнений. Почему я так жестоко поступаю с математикой? Ради результата, когда это является логическим завершением области распространения общих правил. Чем глубже я погружаюсь в неизведанное, тем больше нового и интересного нахожу. В такой ситуации очень сложно закончить работу над чем-то, что еще вчера казалось простым и понятным.

Я очень плохо знаю математику, которая мне не интересна. Знаете ли вы разделы математики, в которых единица в нулевой степени равна нулю?

2 в ноль пятой степени

Сколько будет 2 в ноль пятой степени? Вопрос с подвохом, как и всё то, что придумывают для нас математики. Если кратко, преобразования выглядят вот так.

2 в ноль пятой степени

А теперь разберемся более подробно в логике математиков.Возведение числа в целую степень - это умножение этих чисел. Возведение числа в дробную степень - это извлечение корня из числа, при этом число в знаменателе показывает, корень какой степени нужно найти. А вот саму дробь можно записать и в виде десятичной дроби, и в виде обычной дроби. Засыпаем всё это в горшок, тщательно перемешиваем и математический ребус для учебника готов.

Разгадывать этот ребус нужно в следующем порядке. Переводим десятичную дробь ноль пять в обычную дробь и получаем одну вторую. Вот теперь мы число 2 с показателем дробной степени можем записать как квадратный корень из двух и вычислить его значение.

Для закрепления пройденного материала, рассмотрим ещё парочку простых примеров.

4 в ноль пятой степени

4 в ноль пятой степени - это тоже самое, что и 4 в степени одна вторая. Четыре в степени одна вторая - это квадратный корень из 4. Извлекая квадратный корень из четырех, мы получаем два.

25 в ноль пятой степени

После рассмотрения двух предыдущих примеров, 25 в ноль пятой степени для нас не представляют никого труда. Как заправские шаманы, мы ноль пять превращаем в одну вторую, извлекаем квадратный корень из 25 и получаем такой желанный результат - корень из двадцати пяти равен пять.

Зачем все эти пляски шаманов с бубнами? У этой математической медали есть две стороны. Лицевая сторона - математики учат нас пользоваться математикой. Обратная сторона медали - если математики будут просто и ясно выражать свои мысли на языке математики, тогда они не будут казаться нам такими умными, а мы сами не будем выглядеть такими дураками.

101 в кубе. Как не надо делать.

Как найти 101 в кубе, используя формулы сокращенного умножения? Я уже показывал, как при помощи формулы куба суммы можно вычислить сто один в кубе. Там я одно число 101 представил в виде суммы двух чисел 100 и 1. Использование более простых (более удобных в вычислениях) чисел облегчает вычисление.

На просторах Интернета я увидел другой пример применения формул сокращенного умножения, а именно сумму и разность кубов. Предупреждаю сразу, так не надо делать. Для нахождения 101 в кубе там берут числа 101 и 100. Вот как это выглядит.

101 в кубе. Как не надо делать.

Почему так не надо делать для нахождения 101 в кубе? Сейчас я вам покажу. Я не буду брать числа 101 и 100, я возьму другую пару: число 101, куб которого нам нужно найти, и ноль (у меня уже язык не поворачивается называть ноль числом). Смотрите, что получилось у меня.

101 в кубе. Убираем мусор.

При помощи нуля я убрал из вычислений весь математический мусор. Ведь вместо двух умножений (это возведение числа в куб) какой-то умник нам предлагает выполнять ещё четыре умножения и четыре сложения или вычитания. С чем это можно сравнить? Все знают, что из одной комнаты в другую, соседнюю, можно пройти через дверь. Но вот нашелся человек, который предлагает вылезть в окно в одной комнате и залезть в окно в другой комнате. Да, так можно можно сделать, но зачем?

Я понимаю, что когда математикам делать нечего, они занимаются вычислениями, но лучше бы они брали пример с котов.

Сто один в кубе

Сегодня мы разберем пример, как при помощи формул сокращенного умножения можно найти сто один в кубе. Другими словами, как число 101 возвести в третью степень при помощи формулы сокращенного умножения.

В комментариях раздался вот такой крик о помощи:

Помогите пожалуйста, задача (пример) из физ-мата 8 класс:

101^3

Я не понимаю, как это решить с помощью формул сокращённого умножения.

Возвести число 101 в куб очень просто - нужно набрать число 101 на калькуляторе и два раза умножить на такое же число 101.

101^3=101*101*101=1030301

Если под рукой нет калькулятора (мало ли, телефон только что украли), то можно вычислить на бумажечке в столбик (картинка будет в конце, как проверка и калькулятора, и формулы).

Применяем формулу сокращенного умножения.

В условии задачи сказано, что нужно не просто найти куб числа 101, а применить для этого формулу сокращенного умножения. По мнению учителей математики, эти формулы должны знать все. Наивные. А если вы не знаете, где её взять?

Можно поискать в Интернете по запросу формулы сокращенного умножения. Есть у меня прямо здесь такая страница, если она не нравится - Гугл вам в помощь. Можно эти формулы найти в справочнике по математике, в учебнике по математике за какой-то там класс (врать не буду, а искать лень), можно спросить у знахарая-одноклассника, который знает формулы сокращенного умножения наизусть. Нужная нам формула сокращенного умножения называется "Куб суммы". Ниже вы её увидите.

И теперь ответ на самый каверзный вопрос: как из одного числа получить сумму чисел? Нужно это число разложить на слагаемые. С точки зрения математики, количество слагаемых может быть любое, но... Формулы сокращенного умножения для возведения суммы в куб я нашел только для двух и трех слагаемых. Формула куба суммы трех слагаемых - это просто лютая жесть. А вот куб суммы двух слагаемых выглядит даже симпатично. Основной принцип разложения на слагаемые для применения формул сокращенного умножения заключается в том, чтобы числа можно было легко перемножать в уме, не используя калькулятор. Для числа 101 самым лучшим вариантом будет 101=100+1. Сто и единичку без проблем можно перемножать в уме. Давайте посмотрим, что у нас получится.

Сто один в кубе

Не знаю как вы, но я без бумажки обойтись не смог. Да, записывал я всё в строчку, а не в столбик, но тем не менее. И в заключение, выполним проверку нашего решения, умножив в столбик на бумажке.

Сто один в кубе в столбик

Ну, как-то так. Зачем всё это нужно вам? Чтобы вы знали, что умножать можно не только на калькуляторе или в столбик, но иногда можно эффективно применять и формулы сокращенного умножения. Если, конечно, вы их знаете.

Неизвестная степень числа

Меня тут попросили решить одну задачу, в которой нужно найти неизвестную степень числа. Собственно, не саму задачу решить, а принять участие в решении. Суть задачи такова. Есть два числа, которые имеют такой вид:

Два числа в неизвестной степени

О степени этих чисел нам известно:

1) количество разрядов в числе;
2) первые насколько цифр числа.

Задача: как, хотя бы приблизительно, определить, во сколько раз первое число больше второго?

Отношение чисел

Специально для работы со степенями чисел математики придумали такой инструмент, как логарифмы. Поскольку я в логарифмах мало сто понимаю и разбираться в этом у меня нет ни малейшего желания, мы пойдем другим путем.

Среда нашего обитания оказывает очень сильное влияние на образ нашего мышления. Христианство - это единобожие (в "теорию" о триединстве Бога вдаваться не будем, кто её придумал, пусть тот  и исповедует). К неизвестному числу икс мы автоматически относимся как к божеству - для нас оно едино и неделимо. Вспомним язычников. У них было множество богов на все случаи жизни. К чему это я? К тому, что наше неизвестное число состоит из отдельных цифр в позиционной системе счисления. Часть этих цифр нам известна, часть - нет. А дальше - совсем просто.

Предположим, что наше неизвестное число имеет семь разрядов, три первые из них нам известны. В этом случае мы можем записать число в позиционной системе следующим образом:

Позиционная запись числа

Если вместо знаков вопроса мы запишем цифру "ноль", мы получим наименьшее возможное число. Если вместо знаков вопроса мы запишем цифру "девять", мы получим наибольшее возможное число. Теперь мы можем легко записать пределы значений наших чисел a и b. Отношения этих чисел так же будут находиться в определенных пределах.

Значения чисел

Если известен алгоритм поиска следующего разряда неизвестной степени числа по известному отношению этих чисел, то можно применить метод капитана Врунгеля. Для ускорения изучения английского языка он предлагал нанять двух учителей: один обучает от начала к концу, второй - от конца к началу; когда они сходятся на середине - вы уже знаете весь английский язык :))). В нашем случае можно запустить сразу два алгоритма, если компьютер справится с такой задачей.

Где может быть полезно такое решение? В программировании, робототехнике и бог весть где ещё.

P.S. Оценка результата оказалась такой

Оценка решения

Вот какой диалог по уточнению условия задачи состоялся накануне

Уточнение условия задачи

Не зря умные люди говорят, что правильная формулировка условия задачи - это половина решения.

Два в минус второй степени это

Иногда я подглядываю, что именно вы ищете в интернете и, в частности, на этом сайте. Один из вопросов звучит так: два в минус второй степени это... это одна четвертая. Вот какой я умный. Сейчас. А ещё десять минут назад я прочитал этот вопрос и подумал: "Блин, а это скоко?" Дробные показатели степени, отрицательные... Так сразу и не вспомнить. Десять минут изучения математического справочника - и вот я уже весь такой умный....

Знак минус в показателе степени означает обратное число, то есть дробь, у которой в числителе единичка, а в знаменателе само число. Ну, сейчас у математиков мода такая - лепить, что не попадя, в показатель степени.

Два в минус второй степени это...

Как видите, всё довольно просто. Если в показателе степени нет никаких знаков, значит это хорошая степень и прятать ничего никуда не надо. Если в показателе степени стоит знак минус - это плохая степень и число нужно спрятать, куда подальше. Дальше знаменателя в математике ничего нет. Вот туда число и опускаем. В числителе всё это маскируем единичкой. Поскольку наше число надежно спрятано в знаменателе, знак из показателя степени можно выбросить. Если знак минус не выбросить, число обратно вылезет из знаменателя. Кому это нужно? А никому не нужно. Пусть число сидит там, куда его Родина послала. Уточнять вопрос о том, чья это Родина, мы здесь не будем. Герои-подпольщики и вражеская подпольная агентура - это другая тема в учебниках математики.

Экспонента на калькуляторе

Что такое экспонента и с чем её едят, мы разберемся в следующий раз (вру как путин - следующего раза, скорее всего, уже не будет, вдохновение кончилось). Сейчас мы разберемся, как где находится экспонента на калькуляторе и как её на калькуляторе считать. Нажимайте на ссылку, калькулятор откроется в новом окне. Приступим к практическим занятиям. Нажимайте на те же кнопочки, что нажимал я и смотрите на результат.

Для начала возведем число е в степень 4. В начале нужно набрать показатель степени. Нажимаем на кнопочку 4. Результат нашего вмешательства в беззаботную жизнь калькулятора можете посмотреть на картинке.

Экспонента на калькуляторе

После этого нажимаем на специальную кнопочку экспоненты, обозначенную на калькуляторе е в степени х. Как видно из рисунка, калькулятор нас правильно понял и отреагировал именно так, как нам нужно.

Экспонента на калькуляторе

Для вычисления заданного нами примера экспоненты необходимо нажать кнопочку равно.

Экспонента на калькуляторе

Всё, мы получили требуемое значение.

е⁴=54,598

Общий порядок нахождения экспоненты на калькуляторе такой: набираете показатель степени, потом нажимаете специальную кнопку е^х и кнопку =, результат готов. Можно поступить наоборот - сперва нажать кнопочку экспоненты е^х, после этого ввести значение показателя степени и нажать кнопку равно. Для показателей степени в виде целях чисел или десятичных дробей оба варианта одинаковы. Если же показатель степени задан обыкновенной дробью, то лучше пользоваться вторым способом. Сперва нажимаете кнопку экспоненты, потом вводите числитель дроби, нажимаете кнопку деления, вводите знаменатель дроби и нажимаете кнопку равно. На этой странице мы рассмотрим первый способ.

Для начала вычислим е в первой степени. Собственно, это и будет значение числа е. Напомню, что любое число в первой степени равно самому себе. Порядок нажимания кнопочек пронумерован на картинке красными цифрами.

Экспонента на калькуляторе

Мы получили округленное до 14 знаков после запятой значение числа е:

е¹=е=2,71828182845905≈2,718

Число е подчиняется всем свойствам степени, как и любое другое число. Результаты возведения его в степень такие же, как у чисел больших единицы. При возведении в степень больше единицы результат будет больше первоначального. Для примера, возведем число е в не целую степень 9,876. Порядок нажимания кнопочек показан красными цифрами, результат виден на картинке.

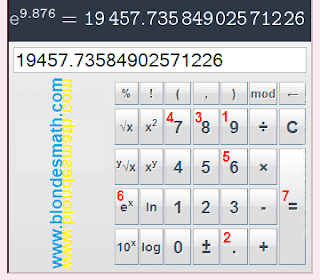Экспонента на калькуляторе

Если показатель степени меньше единицы но больше нуля, то результат получится меньше первоначального но больше единицы. Это соответствует извлечению корня из числа е. Если на калькуляторе ввести показатель степени 0,5 (что равнозначно 1/2) то мы найдем квадратный корень числа е. Мы для примера возьмем экспоненту в степени 0,123

Экспонента на калькуляторе

По логике, дальше следует показатель степени 0. Число е, как и любое другое число в нулевой степени, равняется единице. Это мы знаем и без калькулятора.

е⁰=1

Теперь переходим к отрицательным показателям степени экспоненты. Знак минус возле степени означает обратное число, то есть единицу, деленную на число е в указанной степени, но уже без знака минус. Умный калькулятор это понимает и без наших подсказок - он отлично справляется с отрицательной степенью. Для начала вычислим е в минус первой степени. Смотрим на картинку.

Экспонента на калькуляторе

Мы получили число, обратное числу е:

е^-1=1/е¹=1/e=0,36787944117144≈0,368

Дальше пробуем добыть экспоненту со степенью меньше минус единицы.

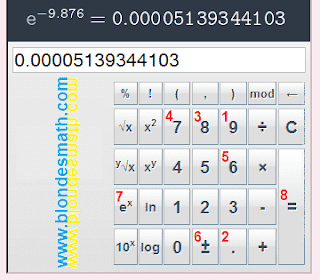Экспонента на калькуляторе

Здесь полученный результат нужно преобразовать в удобоваримый для математиков вид. Делается это так:

е^-9,876=1/е^9,876=1/e=0,00005139344103≈5,139*10^-5

Если после полученного на калькуляторе результата нажать ещё раз на знак равенства, десятичная дробь преобразуется в обычную дробь. Результат этой хитрой операции виден на картинке.

Экспонента на калькуляторе

Но этот результат мне не нравится. Одна тысячная почти в два раза больше пяти десятитысячных. Если бы программа с калькулятором была русской, я бы подумал, что эту функцию писал бывший госслужащий, привыкший всё увеличивать в два раза (нужно же откуда-то себе воровать). Остается только предупредить, что и калькулятору полностью доверять нельзя, нужно самому анализировать результат, который он выдает.

В заключение найдем экспоненту с показателем степени больше минус единицы, но меньше нуля.

Экспонента на калькуляторе

Теперь попробуем преобразовать результат в обычную дробь.

Экспонента на калькуляторе

На этот раз калькулятор выдал более красивый результат. Но я уже ему не верю. Проверим результат преобразования, разделив на калькуляторе числитель на знаменатель. Результат деления записан ниже экспоненты.

Экспонента на калькуляторе

Вот теперь можно поверить калькулятору, поскольку погрешность преобразования совсем незначительная. Округление даже до пяти знаков после запятой дает одинаковый результат.

Что делать, если вы пользуетесь виндосовским калькулятором и даже в инженерном варианте нет заветной кнопочки "е в степени икс"? Найдите кнопочку "Inv", рядом с ней есть кнопочка натурального логарифма "ln". Смело нажимайте кнопочку "Inv".

Экспонента на калькуляторе Виндовс картинка 1

После нажатия этой кнопочки, расположенная рядом кнопочка натурального логарифма волшебным образом превратится в кнопочку "число е в степени икс".

Экспонента на калькуляторе Виндовс картинка 2

По замыслу создателей калькулятора, такие превращения натурального логарифма и ежу понятны. Но...

Во-первых. Ёжик должен быть трезвым.

Во-вторых. Ёжик должен быть сообразительным.

В третьих. В памяти ежа на первом месте должны бить свойства натуральных логарифмов, а не какая-то ерунда типа любви, смысла жизни или завтрашнего урока по математике.

Что касается меня. Я редко бываю трезвым - это раз. Иногда я ужасно туплю - это два. Для меня смысл математики гораздо важнее свойств каких-то там логарифмов - это три.