Случайно попав на сайт , я решил посмотреть, что интересного для блондинок здесь можно безвозмездно позаимствовать (проще говоря - стырить). Методом научного тыка в случайно выбранную кнопочку я оказался на странице . Вот что я увидел.
 |
| Решение системы линейных уравнений онлайн |
Шесть окошечек с ноликами говорили мне о том, что туда надо что-то ввести. Соскребя по сусекам природного склероза остатки своих знаний по системам уравнений и одним глазом подглядывая на расположенный ниже пример системы линейных уравнения, я понял, что мне нужно ввести циферки. Желательно, циферки разные. Насколько я помню, эти циферки в линейных уравнениях называются коэффициентами.
Из первой строчки я решил нолики добросовестно удалить и заменить циферками. Теперь нужно было вспомнить, какие циферки я знаю. Так, "один" помню - это в первое окошко... Помню "два" - во второе окошко... Вот проклятый склероз! В третье окошко я, по инерции, снова ввел циферку "один"... Вау! Есть же ещё циферка "пять"!!! Её я добавил к единичке и у меня получилось число пятнадцать. С первой строчкой я покончил.
Удалять нолики из ячеек второй строчки мне уже было лень, по этому я просто добавил перед ними циферки "один", "два" и снова "один". Всё, система уравнений составлена и я смело нажал кнопочку "Ввод".
Словно после волшебного "Сезам, откройся!", передо мной появилась страничка с решением составленной мною системы линейных уравнений. Решение расписано до малейших подробностей, даже мне всё было понятно. Вверху красовались два моих уравнения, ниже был описан ход решения с пояснениями и вычислениями. Как в школьном учебнике...
В первом уравнении выражаем "х" через "у"... После этого полученное выражение подставляем во второе уравнение и находим значение "у"... Для того, что бы найти значение "х", нужно значение "у" подставить в одно из уравнений системы, например в первое уравнение... В результате решения системы двух линейных уравнений с двумя неизвестными мы получили значение "х=15", значение "у= "
Я лениво просматривал текст решения, любуясь красотой буковок и циферок, как вдруг... СТОП!!! От неожиданности я даже проснулся. Мои глаза застыли на том месте, которое вывело меня из гипнотического транса. В значении "х" после знака равенства стояло число 15. В значении "у" после знака равенства было ПУСТОЕ МЕСТО! Я ничего не понимал... Как баран на новые ворота, я смотрел в пустоту после знака "равно". Беглый взгляд вверх - в решении, кажется, всё правильно. Везде стоят циферки, как и положено... Потом я медленно перевел взгляд в торону, где было представлено графическое решение системы уравнений... Тут я всё понял - на графике красиво вырисовывались две параллельные прямые.
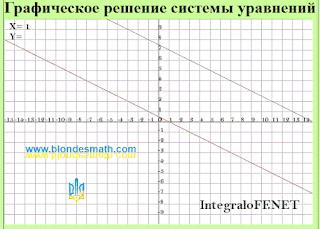 |
| Графическое решение системы уравнений |
Я уже начал догадываться, что произошло. Внимательно просмотрев решение, я быстро нашел причину - деление на ноль!
 |
| Решение системы линейных уравнений |
Видите первую красную черточку на рисунке? После "у" равно стоит число, которое делится на ноль, после этого стоит ещё один знак равенства, а дальше ... пустота! В расчетах ниже, там, где должно стоять значение "у", везде пустое место. И, тем не менее, значение "х" победоносно найдено!!!
Да уж, в Интернете насмотришься всякого... Деление на ноль - это кошмарный сон любого программиста. Лично я впервые встречаю сайт, где деление на ноль просто игнорируется. Больше того, это проигнорированное решение участвует во всех дальнейших расчетах и позволяет получить вполне конкретный результат! Внимательно присмотревшись к концовке расчетов, я понял уловку программистов. Они приняли собственную математическую аксиому, которая гласит: "проигнорированное решение умноженное на число равняется нулю. Но, поскольку, эта аксиома является их личным изобретением и в математических священных текстах не значится, они стыдливо спрятали нолик подальше от наших глаз.
Как математик, могу вам сказать, что в подобном случае решение системы уравнений прекращается сразу же после появления деления на ноль. Деление на ноль указывает на то, что для дальнейшего решения этой системы уравнений нужно переходить к математическим методам деления на ноль. Как это записывается на математическом языке, мы с вами в недалеком будущем разберемся. На человеческий же язык это можно перевести приблизительно так: "Думай хоть немного! Только полный идиот может искать координаты точки пересечения двух параллельных прямых". Покуда же у математиков принято говорить "система не имеет решений".
После всех этих математических раскопок, я, наконец-то, задался вопросом: "А что же, собственно, за уравнения я написал?". Посмотрев внимательно на исходную систему уравнений, лениво придуманную мною, пришлось согласиться с математикой - я полный идиот. Если второе уравнение разделить на 10, то получим систему из таких уравнений:
х+2у=15
х+2у=1
Дальше пошел уже чисто спортивный интерес и рысканье по математическому справочнику в поисках ответа. Как видно из уравнений, они действительно являются уравнениями параллельных прямых.
Но вернемся к программистам. Сперва я подумал, что это полные тупицы. Но когда я открыл из закладок новую вкладку со страницей этого сайта, что бы дать вам ссылку на главную страницу... Вау! Я увидел вот это...
 |
| Мы всё можем |
Вот пример математического оптимизма! Да, девиз настоящих математиков должен звучать именно так: "Мы такое пока не умеем решать, но скоро научимся". Без всяких "решение не возможно", "не имеет смысла". Эти слова для тупых бездарных посредственностей.
Вот после этого я восхитился программистами. Они убрали из вычисления и из программы ошибку деления на ноль. Они временно ввели свою аксиому. Они полностью сохранили ход решения системы линейных уравнений. Да, сегодня они не знают, чему равен результат деления на ноль. Но если завтра этот результат станет известен, им останется только ввести его в уже готовую программу и у них всё будет работать, теперь уже и с делением на ноль.
Если к математическим знаниям и математическому оптимизму этих ребят добавить прямолинейную логику блондинок... Все задачи в математике будут решены. Пусть и не сразу. Ведь мы не Боги, мы только учимся...
мужик, ты прав, но всем все п%$#й.
ОтветитьУдалитьможет тебе п*х*й а мне нет
УдалитьЯ так понимаю, что себя ты ко "всем" не относишь, поскольку не поленился написать здесь комментарий. Вот видишь, нас уже двое. Кому ещё не безразлично то, чему их учат?
ОтветитьУдалитьДа уж, интересно будет посмотреть как они найдут решение несовместной системы! Вот уж точно будет переворот в математике!
ОтветитьУдалитьХотя, кто знает, про теорию относительности Эйнштейна тоже говорят, что она не верна, так что возможно параллельные прямые и пересекутся когда-нибудь! Мало ли.
Я знаю, где искать решение этой системы и как оно выглядит.
ОтветитьУдалитьМне тоже есть что сказать про Эйнштейна и это многим может не понравиться.
Лет 30 назад я написал стишок, который звучал приблизительно так:
Альберту Эйнштейну
Как ураган, ворвавшись в мир,
Разрушил рай Ньютона.
Полеты к звездам запретил
Ты нам своим законом.
В подвалах старится портвейн,
Года летят быстрей фотона...
И на тебя, как на Ньютона,
Найдется свой Альберт Эйнштейн.
Я уже делаю с теорией Эйнштейна то же самое, что он сделал с теорией Ньютона)))
Я, конечно верю, что для Вас нет ничего проще, однако хочу отметить, что 95% людей с Евклидовым пространством нелегко, а Вы тут выдаете всякие страшности. Но с другой стороны, нужно знать, что есть еще и другие возможности(в данном случае пространства). Так что считаю, к проблеме требуется индивидуальный подход!
ОтветитьУдалитьМаня во всей этой заварушке с параллельными прямыми интересует не решение системы уравнений, а совсем другой вопрос. То решение, которое могу предложить я, ничего интересного не даст.
ОтветитьУдалитьЗдрасьти ))) объясните плиииз как решается такое уравнение:
ОтветитьУдалить2А+2В=0
А-В=1
не могу понять с какого перепуга А=1/2
А-В=1 отсюда А=В+1
ОтветитьУдалитьПодставляем второе уравнение в первое
2(В+1)+2В=0
2В+2+2В=0
4В+2=0
4В=-2
В=-2/4=-1/2
Теперь возвращаемся назад, первой строчке
А=В+1=(-1/2)+1=1/2
Вот с этого перепугу, который я специально в скобочки посадил, как в клетку, у нас А получается равным половинке.
Если подставить полученные нами значения в уравнения, получим
2*1/2+2*(-1/2)=1-1=0 0=0
1/2-(-1/2)=1/2+1/2=1 1=1
что и требовалось доказать ;)
а можно делать так: в выражении 2А+2В=0 сократить 2 (все равно же оба числа умножаюцо на одно и тоже число, им что жалко что ли), получится А+В=0 и взять второе выражение А-В=1 и соединить левую и правую части:
ОтветитьУдалитьА+В+А-В=1
можно делать так всегда?
Да, можно. Красиво и изящно получается. Я не додумался :) Главное - что бы результаты совпадали. Если мы что-то сделаем, а результат получится другой - значит так делать нельзя :)))
ОтветитьУдалитьа мне не поможете?
ОтветитьУдалитьСоставьте уравнение эллипса,проходящего через точки A(sqrt5;sqrt7) и B(sqrt10;sqrt5),если его фокусы лежат на оси абсцисс.
К сожалению, я уже не помню, как это делается.
ОтветитьУдалитьЗдравствуйте!) помогите пожалуйся решить систему (ху-1)^2-3([y-1)-28=0
ОтветитьУдалитьx-3y=2
Во втором уравнении можно выразить Х через У
ОтветитьУдалитьх=3у+2
Потом это можно подставить в первое уравнение. Если мы с первым уравнением начнем проделывать какие-то штучки типа преобразований, то уравнение должно упроститься (а иначе какой смысл его запутывать, если невозможно будет распутать).
Можно сразу попробовать упростить первое уравнение, возведя первое выражение в квадрат. Скобки уберутся, 28 превратится в 27, потом посмотреть, что можно сделать дальше.
Короче, я блондинка, а не вундеркинд))) На ответах mail.ru могут такое в миг решить, если, конечно, захотят.
Я по ошибке не тот комментарий удалил. Вот система уравнений
ОтветитьУдалить(ху-1)^2-3(xy-1)-28=0
x-3y=2
Эту штуку нужно решать путем подстановки (подтасовки фактов))))
ху-1=z
Первое уравнение примет вид
z^2-3z-28=0
Решаем его как обычное квадратное уравнение и находим z. Пусть у нас получилось бибиби. Тогда наша система уравнений примет вид
ху-1=бибиби
x-3y=2
ху=бибиби+1
х-3у=2
Вот теперь выражаем во втором уравнении Х через У, подставляем в первое уравнение и победоносно доводим решение до конца. Честно, мне просто лень со всем этим возиться.
спасибо огромное!))
ОтветитьУдалитьПожалуйста, обращайтесь. Вдруг я ещё что-то умное знаю, кроме системы уравнений и таблицы натуральных чисел :)))
ОтветитьУдалитьЯ видела этот сайт, и увидела, что знаки там не поменять. Допустим мне нужен минус?:( А там его нет.
ОтветитьУдалитьЯ попробовал ввести в ячейку числовой коэффициент перед неизвестным со знаком минус, например -21. Приняло нормально и выдало решение стандартное, где в математических действиях с отрицательным числом стоит подряд два знака минус 12--21, что должно переводиться на нормальный язык как знак плюс. Скорее всего, разработчики не захотели сильно усложнять программу решения системы уравнений. Ведь чем проще, тем надежнее работает.
ОтветитьУдалитьСпециально взял пример с решением и проверил - да, это работает и ответ получается правильный:
Значение x =2
Значение y =-2
Единственное, ход решения нужно переписывать внимательно, вот что выдает сайт, например (один из коэффициентов был равен -2):
3·x + 1·-2 =4 (надо 3х-2=4)
3·x =4 - 1·-2 (надо 3х=4+2)
x =(4 - 1·-2)/3 (надо х=(4+2)/3
x =(4 - 1·-2)/3
x =(6)/3
x =2
Каким должно быть значение А чтобы функция находилась ниже оси абсцис у=-х*х+6х+А
ОтветитьУдалитьМеня уже очень давно не дрессировали на подобных уравнениях, по этому ничем помочь не могу :)
ОтветитьУдалитьпомогите пожалуйстра решить систему уравнений))
ОтветитьУдалитьфигурная скобка:
x+y=5
xy=6
Их второго уравнения достаем
ОтветитьУдалитьу=6/х
Всовываем это в первое уравнение
х+6/х=5
умножаем на знаменатель всё выражение
х^2+6=5х
Приводим к такому любимому нами виду
х^2-5х+6=0
А дальше решать нужно по типу того, как написано выше. Сперва решаем квадратное уравнение, а потом то, что осталось.
помогите ,пожалуйста решить(это система уравнений, просто обобщающей скобки нет.)
ОтветитьУдалить(3x-2):(4y+3)=4:15
(5x-y):(3y-2)=1
Математикой пользоваться умеете? Свойства пропорции помните? Произведение крайних членов пропорции равно произведению средних членов. Раскрываем скобки, потом перегоняем всех этих баранов в одно стойло. Получаем уравнения в удобоваримом виде.
ОтветитьУдалитьПервое уравнение пошло:
15(3х-2)=4(4у+3)
45х-30=16у+12
45х-16у-42=0
Второе:
5х-у=1*(3у-2)
5х-у=3у-2
5х-4у+2=0
Получилась система уравнений в любимом ними виде:
45х-16у-42=0
5х-4у+2=0
Вру. Это мой любимый вид. Для них, оказывается, нужно подавать в другом дизайне:
ОтветитьУдалить45х-16у=42
5х-4у=-2
Вот теперь это можно всунуть, как дрова в печку, в онлайн сервисы и получить решение. Не забываем про знаки минус перед числами. По дырочкам это выглядит так:
(45)х+(-16)у=(42) вставляем 45; -16; 42
(5)х+(-4)=(-2) вставляем 5; -4; -2
Победоносный результат выглядит так:
х=2
у=3
Решение передирайте с сервисов, проверка показывает, что первый сервис умеет правильно решать уравнения. Второй сайт я тревожить не стал, пусть отдыхает)))
Большое спасибо!
ОтветитьУдалитьх=-у+4
ОтветитьУдалитьу2+3ху=18
Ход решения описан на странице "Решение системы уравнений подстановкой", нужно только чуточку подумать. Маленькая подсказка y^2-3y^2=-2y^2
Удалитьx2+2xy=16
ОтветитьУдалить4x-y=5
x2+y2=29
xy=10
Здравствуйте помогите решить.... я уже измучилась...
ОтветитьУдалить(1+4x)(1+5x)(1+9x)=81(9+4x)(9+5x)(1+x)
Если это для школы, тогда понятия не имею. Если нет, то тупо всё перемножаем, получаем (если я не ошибся):
Удалить180х^3+101x^2+18x+1=
=1620x^3+8181x^2+13122x+6561
это приводим к каноническому виду кубического уравнения
1440x^3+8080x^2+13104x+6560=0
Потом идем по ссылке и решаем кубическое уравнение. Решение там явно не детское, на целую диссертацию.
Спасибо Вам большое! Я даже разобралась в решении)))
УдалитьСнимаю шляпу перед умом и настойчивостью)))
Удалитьпомогите решить пожалуйста
ОтветитьУдалитьR1= 1,5R2+0,5
1,5R2=2R3+0,5/1,5
R1= 2R3+1
Не надо бояться внешнего вида, нужно бояться сути: все самые красивые существа - смертельно опасны; все самые приятные слова - лживы :)))
УдалитьИз первого и последнего
1,5R2 = R1-0,5
2R3 = R1-1
Эти фрагменты заменяем в среднем уравнении
R1-0,5 = R1-1+(0,5/1,5)
R1-R1 = 0,5-1+(1/3)
0 = -(1/2)+1/3
0 = -1/6
С другой стороны, последнее подставляем в первое и приводим к виду среднего для сравнения
1,5R2 = 2R3+1-0,5
1,5R2 = 2R3+0,5
Получается, что у нас имеется два уравнения
1,5R2 = 2R3+1/3
1,5R2 = 2R3+1/2
Отсюда получается, что одна и та же величина R2 в разных уравнениях имеет разные значения, что не может выполняться для двух уравнений одновременно. Следовательно, решений нет.
Помогите пожалуйста решить систему уравнений
ОтветитьУдалитьХ1+Х2=3
Х1-Х2=-1
Преобразуем уравнение в человеческий вид:
УдалитьХ1=х
Х2=у
Получем:
х+у=3
х-у=-1
Коэффициенты этой системы уравнений такие:
1; 1; 3;
1; -1; -1.
Проходим по ссылке, вставляем эти числа в соответствующие ячейки и получаем готовое решение. В решении не забываем -1 брать в скобки (-1).
Ответ:
Х1=1
Х2=2
9у=2у решите,пожалуйста
ОтветитьУдалить9у=2у
Удалить9у-2у=0
7у=0
у=0/7
у=0
спасибо!!!
Удалитья вобще не могу со сло справится(( не понимаю
ОтветитьУдалитьсистема
9:ху-4:(х+у)
{
6:(х-у)+12:(х+у)=8
Вспоминаем школу. Нужно каждое из уравнений привести к общему знаменателю. Тогда знаменатели смело можно выбросить в мусор. У нас останутся два уравнения обычного вида, без дробей. Смотрим, что с ними можно сделать и как их решить.
ОтветитьУдалитьСейчас я занят, решать некогда:(
здравствуйте!помогите пожалуйста.система уравнений метод новых переменных
ОтветитьУдалить3/x-y+6/x-y=-1
5/x+y+9/x-9=-2
Вынужден вас огорчить, но я понятия не имею ни о методе новых переменных, ни о методе старых переменных (по логике, такой должен был быть). Меня интересует самая примитивная математика, а не разные современные методы решения придуманных кем-то задач.
Удалитьпомогите пожалуйста решить СИСТЕМУ
ОтветитьУдалить1.{(х-3)(2 степень)-у=0
{х+у=8
2. {ху=-2
{х-2у=5
Результат вычисления системы уравнений
Удалить(x-3)^2-y = 0
x+y = 8
есть:
y = sqrt(21)/2 + 11/2
x = -sqrt(21)/2 + 5/2
и
y = -sqrt(21)/2 + 11/2
x = sqrt(21)/2 + 5/2
Результат вычисления системы уравнений
x*y = -2
x-2*y = 5
есть:
y = -2
x = 1
и
y = -1/2
x = 4
Решения найдены при помощи этого сервиса
В обеих системах во втором уравнении выражаем у через х и подставляем в первое уравнение. Решаем квадратное уравнение и находим х. Потом находим у.
помогите пожалуйста решить систему уравнений:
ОтветитьУдалитьsin x =cos y
2cos^2y+sin x=3
Здравствуйте,помогите пожалуйста решить эту систему)Заранее огромное Вам спасибо)
ОтветитьУдалитьx^2-2y-x=-20
x-y=1
У меня получился ответ:корней нет.Но не знаю,правильно ли это?)
У меня тот же ответ получился, а уравнение имеет вид:
Удалитьx^2-3x+18=0
Неправильно составленное уравнение - это для математиков в порядке вещей. Хотя позже, в высшей математике, они нас будут уверять, что это уравнение имеет 2 комплексных корня:
x1=1,5+3,969i
x2=1,5-3,969i
Помогите, пожалуйста, упростить выражение, ничего не получается
ОтветитьУдалить((x-3)/(4*x^2+24*x+36))/(x/(3*x-9)-3/(x^2-3*x)+(x^2+9)/(27-3*x^3))
И у меня тоже ничего хорошего не получается. Мне очень не нравится выражение в последней скобке (27-3*x^3) Если бы здесь был икс в квадрате, это очень облегчило бы решение. Или тройку убрать перед икс в кубе. Тогда 27 это 3 в кубе и можно применить формулу разности кубов. Я так подозреваю, что в библию закралась опечатка:)
УдалитьРешите систему уравнений 2x=y x+2y=10
ОтветитьУдалитьНу, это для детского сада. Если вас не научили решать такие простые системы уравнений, то что же будет дальше??? Чем у вас преподаватель математики на уроках занимается? Или чем занимаетесь вы?
УдалитьИ так, в первом уравнении нам прямо говорится, что один игрек равняется двум иксам. Перепишем первое уравнение в более удобочитаемом виде:
2x=y
у=2х
Подставим это значение игрека во второе уравнение и у нас получится уравнение с одним неизвестным иск, значение которого очень просто найти. Запишу решение очень подробно, как под микроскопом:
х+2у=10
х+2*(2х)=10
х+2*2х=10
х+4х=10
(1+4)х=10
5х=10
х=10/5
х=2
Икс мы нашли. Теперь нужно найти игрек. В первое уравнение подставляем найденное значение икса и находим, чему равен игрек:
у=2х
у=2*2
у=4
Для проверки мы можем подставить найденные значения икса и игрека в оба уравнения. Если равенство соблюдается, значит система уравнений решена верно. Смотрим первое уравнение:
2х=у
2*2=4
4=4
Равенство выполняется. Теперь проверим второе уравнение:
х+2у=10
2+2*4=10
2+8=10
10=10
Всё сошлось. Мы просто молодцы!