Дано abcda1b1c1d1 - прямоугольный параллелепипед. dd1cc1 - квадрат. dc = 3, bd1 = корень из 22. Найти bc. Доказать, что bcd1 и dc1b1 взаимно перпендикулярны.
Здесь важны два момента:
1. Правильно нарисовать картинку и разобраться, что дано, а что нужно найти.
2. Подобрать нужную формулу для решения.
Начнем с картинки. В условии сказано, что одна из граней - квадрат. Чем знаменит квадрат? У него все стороны имеют одинаковую длину. Так что фактически нам известны две стороны прямоугольного параллелепипеда и диагональ. Нужно найти длину третьей стороны.
 |
| Прямоугольный параллелепипед и диагональ |
Так, что-то квадрат на картинке у меня совсем не получился, но ведь и я не Малевич. Какая картинка под рукой была, ту и разукрасил. Корень квадратный возле диагонали корявый какой-то вышел. Но оно и понятно - сейчас зима, у нас корни не растут. В супермаркет завезли корни из Австралии (там сейчас лето), вон он какой зеленый, не дозрел ещё. Потому и корявый.
Для решения задачи применяем старую добрую теорему дедушки Пифагора для прямоугольного параллелепипеда. Тысячи лет люди нею уже пользуются и останется она неизменной на все оставшиеся времена. Если я, конечно, более общий вид её здесь не опубликую. Но это как-нибудь в другой раз.
Гласит теорема Пифагора следующее: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов измерений (или сторон) параллелепипеда. Какие измерения есть у прямоугольного параллелепипеда? Их три: длина, ширина, высота. Возводим их в квадрат, складываем в кучку, выковыриваем из суммы квадратный корень и получаем длину диагонали. Очень простенький рецепт.
В нашей задаче известны диагональ и две стороны. Найти нужно третью сторону. Жонглируем формулой и находим выражения для определения третьей стороны. Подставляем значения и задача решена.
Теперь о доказательстве. С детства ненавижу доказательства. Доказывать другим, что я не дурак? Глупо. Насколько я понимаю, в данном случае от вас требуется продемонстрировать свои знания признаков перпендикулярности плоскостей. Есть у меня умная книжка по математике и там написано буквально следующее:
Признак перпендикулярности плоскостей.
Теорема 1 (о перпендикулярности). Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
 |
| Перпендикулярные плоскости |
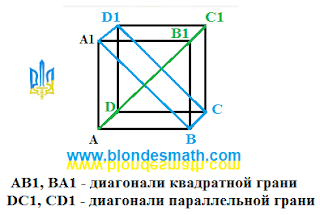
Снова вспоминаем, что я не Малевич. Откуда мы знаем, что указанные плоскости проходят через перпендикулярные прямые? А дядька или тетка в условии задачи написали, что передняя и задняя грани нашего прямоугольного параллелепипеда являются квадратами. А как известно всем, диагонали у квадрата перпендикулярны. В детском садике так учили. Ну, или в школе.
Комментариев нет:
Отправить комментарий