Пропорции

Наконец-то мы добрались до пропорций. В математике пропорции - это самые настоящие пляски шаманов с бубнами. Это нам так говорят, что шаман своими плясками может вызывать дождь. На самом деле шаман смотрит на приметы и только тогда решает, плясать ему или не плясать. Но давайте посмотрим, что математики пишут о пропорциях.

Пропорции

И так, пропорцией математики называют равенство двух отношений. Это Святое Определение пропорции. Тупо учим и говорим его математикам. Если какой-нибудь садист от математики спросит вас "Что такое четвертое пропорциональное?" нужно отвечать "Это один из членов пропорции". А теперь отодвинем проповедников математики в сторону и попробуем сами разобраться, что же это такое - пропорции?

Еще раз. Пропорция - это равенство двух отношений. А что такое отношение? Отношение - это простая дробь. Простая дробь - это рациональное число. Рациональное число - это деление. Деление - это отношение... Короче. Получается, что Маша - это Ксюша, Ксюша - это Люба, Люба - это Таня... Как зовут девочку? А фиг вас поймешь. Вот теперь пора вывести мошенников от математики на чистую воду.

Берем математическую библию и внимательно читаем: "Рациональные числа записываются в виде дробей неоднозначно. Так, дроби

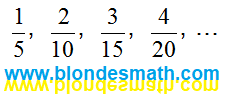Рациональное число

выражают одно и то же рациональное число. Поэтому для записи рациональных чисел употребляют лишь несократимые дроби.

Одно и то же рациональное число может быть записано разными вариантами одной дроби. Математики нас учат сокращать дроби. Как заправские шулеры, в этот момент они прячут туз в рукав. Сокращение дроби - это туз в рукаве. Когда математики достают свой туз из рукава? Когда начинают нам рассказывать о пропорциях.

Пропорция - это одно и то же рациональное число, записанное дважды со знаком равенства.

Пропорция - это банальное расширение дроби. Что такое расширение дроби? Это умножение числителя и знаменателя на одно и то же число.

Дальше у нас будут курсы кройки и шитья. Видите на картинке рядочек дробей? Сейчас мы их запишем чуточку по другому. Дальше берем ножницы, вырезаем две дроби и один знак равенства. Сшиваем это в кучку - всё, пропорция готова.

Расширение дроби и пропорция

Что мы делаем дальше? В старину брали гусиное перо, обмакивали его в чернила и ставили кляксу на одном из чисел в пропорции. Всё, классическая задача на пропорции готова, можно переписывать в учебник. Сейчас аэрозольные баллончики гораздо легче найти, чем гусиные перья и чернила.

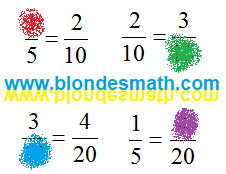Задачи на пропорции

Но в Святом Математическом Писании есть четыре буквы, обозначающие пропорции. Как быть с ними? Возьмем и мы в руки любимые цацки математиков и посмотрим, как из одной дроби получаются две.

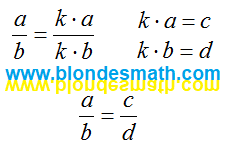Пропорция

Как видите, для наведения тени на плетень математики тупо подменяют две понятные буковки одной непонятной. На этом и держатся страх учеников перед неведомым и могущество пропорций в руках математиков. Ну чем не шаманы?

Что такое буква "k" в наших формулах? Это коэффициент пропорциональности. Именно он превращает одну дробь в пропорцию. Для числителя и знаменателя этот коэффициент пропорциональности одинаковый. Если эти коэффициенты будут разными - никакой пропорции не получится. Это и есть главный секрет математических пропорций.

Коэффициент пропорциональности

Почему в математическом справочнике нет ни слова о коэффициенте пропорциональности? Либо математики сами об этом не знают, либо шаманы свято хранят свои тайны. Ведь с коэффициентом пропорциональности все волшебные свойства пропорций испаряются, как дым. Дым над водой - "Smoke On The Water" группа Deep Purple