Умножение на ноль в геометрии

Рассмотрим умножение на ноль в геометрии. При умножении длины на ширину получается площадь. Что бы вам математики не рассказывали, все формулы площадей любых геометрических фигур сводятся к этой простой формуле. Просто для разных фигур есть разные поправочные коэффициенты, но об этом мы поговорим как-нибудь в другой раз.

И так, у нас есть прямоугольник и формула для нахождения его площади. Традиционно, это изображается так.

Площадь прямоугольника

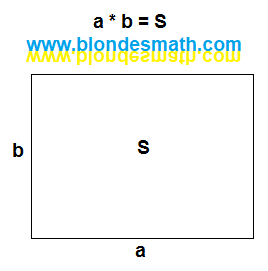
Кажется, всё правильно. Но... В алгебре мы сперва записываем два сомножителя, затем пишем знак равенства и, только после этого, записываем результат умножения. Это целый сериал получается, а не одна картинка. Давайте геометрически изобразим все то, что мы записываем алгебраически. Стороны прямоугольника a и b - это отрезки. Математическое действие умножения геометрического представления не имеет. Знак равенства я заменю вертикальной чертой, разделяющей картинку на две части - до умножения и результат умножения. Площадь прямоугольника S - это, собственно, и есть сам прямоугольник. Вот что получилось.

Умножение в геометрии

Два перпендикулярных отрезка до умножения превращаются в площадь прямоугольника после умножения. Теперь нарисуем умножение на ноль.

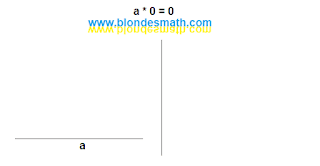Умножение на ноль

В результате умножения на ноль мы площадь не получаем. Длина у нас есть, а вот ширина отсутствует. Естественно, площади просто неоткуда взяться. Смотрим на результат умножения нуля.

Умножение нуля

Теперь у нас есть ширина, но отсутствует длина. Снова площадь получить невозможно. Дальше изображаем умножение нулей - ноль, умноженный на ноль, равняется нулю.

Умножение нулей

Ни длины, ни ширины, ни площади. Ничего не берем, умножаем ни на что и в результате ничего не получаем. А теперь самое интересное.

Давайте попробуем изобразить геометрически тот интимный момент, когда мы умножения не выполняем. Даже алгебра стыдливо умалчивает об этом. Как алгебраически записать тот факт, что у нас имеется два отрезка, которые можно трактовать как длину и ширину, но математическое действие умножения между ними мы не выполняем? Ни одному дураку такое в голову не придет, вот дураков этому и не учат. Разумные существа отличаются от дрессированных животных тем, что они могут делать не только то, чему их научили дрессировщики. Нас приучили к тому, что умножение мы выполняем только по команде "Бобик, умножай!" или когда видим знак умножения, все остальные случаи мы просто игнорируем. Вот по этому в математике символ "не умножай" отсутствует. Вместо него я использую союз "и".

Умножение не выполняем

Если мы умножение не выполняем, площадь отсутствует. Вот теперь мы можем сравнить полученные результаты. Если мы выполняем умножение, то в результате получается площадь. Если мы умножение не выполняем, площадь отсутствует.

Вывод: при действиях с нулем математическая операция умножения не выполняется.

Выполнять умножение с нулем можно, только выполнить его нельзя - не получится. Это как пилить воздух. Вы берете в руки пилу, двигаете нею взад-вперед и всем по телефону рассказываете, что вы пилите. Только при этом не уточняете, что пилите вы то, что в принципе распилить невозможно. Кстати, физику умножения на ноль мы рассмотрим отдельно.