 |
| Тригонометрические функции определение на треугольнике |
Это ещё одна икона для вывешивания на стену и заучивания текста. Мы этим заниматься не будем. Лучше посмотрим, как можно совместить прямоугольный треугольник и окружность. Для этого совместим две картинки: окружность из классического определения тригонометрических функций и наш треугольник. Поместим треугольник рядом с окружностью. Вот как это выглядит.
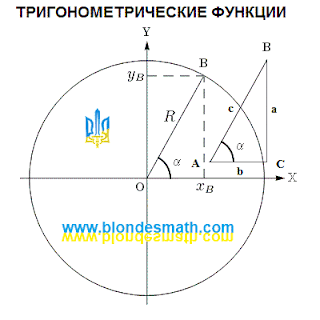 |
| Треугольник и окружность |
Как видите, картинки практически одинаковые, а вот составные элементы в них называются по-разному. Одинаково обозначены только угол альфа и точка "В". Теперь наложим треугольник прямо на окружность. Все графические изображения, принятые для окружности, мы сохраним, а прямоугольный треугольник подчеркнем красными линиями с внутренней стороны (типа обведем контур треугольника губной помадой).
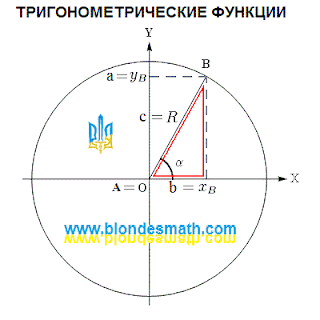 |
| Треугольник в окружности |
Как видно из рисунка, гипотенуза прямоугольного треугольника превращается в радиус окружности, катеты становятся равными координатам точки. Это как в человеческом языке - одно и то же понятие в разных языках обозначается разными словами. Это различие в произношении не дает нам понимать иностранные языки. Приблизительно то же самое происходит в математике. Некоторые считают определение тригонометрических функций на прямоугольном треугольнике примитивным. Если вы хотите понимать математику, запомните следующее: в математике не бывает примитивных вещей. Бывают примитивные существа, считающие себя очень умными. Именно желание казаться умнее других, привело к тому, что математики сами почти ничего не понимают в математике.
Специально процитирую фразу из Википедии, где говорится об определении тригонометрических функций на треугольнике: "Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники". Честно говоря, подобное дремучее невежество математиков меня просто шокирует. Для какого треугольника определяются тригонометрические функции? Правильно, для ПРЯМОУГОЛЬНОГО. Пусть хоть один математик покажет мне ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК С ТУПЫМ УГЛОМ. Клянусь вам, как только я увижу это геометрическое чудо, я тут же переверну портрет тангенса вверх ногами и повешусь на косинусе. Неужели ни один математик не понимает, что решение "элементарных задач про тупоугольные треугольники" при помощи тригонометрических функций ВСЕГДА сводится к разбиению одного тупоугольного треугольника на два прямоугольных треугольника? Научитесь задачи формулировать, а не эти ваши ребусы типа "а угадай, какую фигню я придумал".
Сейчас я вам покажу самый примитивный пример существования тригонометрии в жизни. Примитивнее, наверное, уже не бывает.
 |
| Тригонометрические функции в жизни |
Посмотрите на фото - сколько человеческих тел безмятежно расположилось на горизонтальной плоскости скалы, в то же время на вертикальной плоскости нет ни одного человека. Почему? Да потому, что тригонометрические функции для перпендикулярного направления имеют совсем другие значения. Для нас с вами основным смыслом тригонометрических функций является то, что именно тригонометрические функции определяют наши возможности.
в математике не бывает примитивных вещей. Бывают примитивные существа, считающие себя очень умными....
ОтветитьУдалитьОТЛИЧНО СКАЗАНО!
Чем проще (примитивнее) тем лучше. математика это как бы это странно не звучало, примитивный аппарат, тоесть простой, который позволяет нам на её же примере постигать таинства вселенной.
ОтветитьУдалитьИнными словами математика это аналогия, некая метафора, абстракция, которая переносит реальные вещи на нереальные математические функции, позволящие хуть что-то понять.
А вообще, чем я больше размышляю об логике, математике, тем больше разочировываюсь в них.
Лично моё мнение: "Наука тем точнее, чем меньше в ней математики".
И скоро проаргументирую это высказывание.
Математика это коллективная выдумка, гениальная, прекрасная, но при этом выдумка. Это всё равно что нарисовать арбуз в виде огромного квадрата. Вот примерно так описывает математика реальность. Но лучше пока ничего не придумали и врядли придумают в ближайшее время, пока идёт такой друдом в системе образования, пока люди тупо повторяют, а не думают и делают нечто новое.
Манул, я с тобой не согласен. Не надо смешивать математику (именно ту, которая простая) с коллективной выдумкой (все наши навороты на простоту). Наука - это и есть математика. За исключением философии и, как это не парадоксально, самой математики - это религия. Да, верят там не в Бога, а в законы и определения, но суть от этого не меняется.
ОтветитьУдалитьЧем меньше в науке математики - тем больше она превращается в религию, пределом развития подобной науки является философия)))
Понимаете в чём проблема, я совсем недавно это понял, но мы люди которые думаем, размышляем, филосовствуем и изобретаем, когда гвоорим друг с другом используем вроде одни и те же слова, но наделяем их разным смыслом.
ОтветитьУдалитьМы быть может гвоорим об одной вещи, но таким образом, что слова наши противоречат друг другу.
Через месяц, когда треклятая сессия подёт, я объясню почему так думаю в развернутом виде. Ваше право будет согласиться или наоборот моим словам :)
Разные пути, а цель одна.
Вот например, простейший довод:
Чем мир крупнее тем легче в нём ввести расчёты, потому что цифр меньше. Обычная классическая механика. А вот чем больше всего и факторов, тем больше чисел, чем больше чисел, тем больше округленей и математических операций "макросов". Тем более неточные данные.
Вот и выходит что точные науки использующие математику как можно меньше, более точные, чем те, что состоят из одной математики.
Теория струн ,например...Дурдом ещё тот.
А вот взять например химию, математики там минимум (если обычную, школьнуЮ). Всё понятно и точно работает. Простейшиеи расчёты помогают предсказывать направления и ход реакций. Или вот механика галилейская, тоже неплохая штука. А вот чем дальше тем, бредовее становится мир. И дело не в шаблонности и узкомыслии, просто сама "метафора" неадекватна.
Насчет сложности и неточности. Тут нужно быть существом разумным и уметь находить компромиссное решение. Это задача для идиотов - найти все числа числа ПИ ))) А вот насчет того, что чем больше условий мы вводим в задачу, тем сложнее решение - это точно. В том задача математики и заключается, что бы для сложных процессов найти простые описания.
ОтветитьУдалитьОчень интересная тема, думаю, мы еще не раз к ней будем возвращаться.
Скажите, а возможно ли создать такую систему исчесления в которой не будет дробных чисел?
ОтветитьУдалитьСудя по всему, нет. Единица является точкой симметрии чисел, если есть числа больше единицы, то обязательно есть и числа меньше единицы. Произведение числа и обратного ему числа равно единице. Само обратное число является дробным. Кроме того, сумма числа и обратного ему числа будет давать дробное число в любой системе счисления. Как только мы выбираем единицу измерения чисел (систему счисления), тут же автоматически появляются дробные числа.
ОтветитьУдалитьДоброго времени суток!
ОтветитьУдалитьПодскажите, как ввести определение тригонометрической функции для тупого угла?
Для тупого угла тригонометрические функции определяются через окружность радиуса R и координаты точек окружности.
Удалитьа что если ввести условие что самое маленькая дробь которая только может быть равна 1це? И опирировать числами вместо еденицы например 1а, где а 10 в какойнибудь большой степени?
ОтветитьУдалитьъотя наверное не прокатит
зачем создавать учебники если в них нечего не поймешь без бутылки не разобраться ))) вот и вылазиешь немного за счет теоритических знаний
ОтветитьУдалить