Попробуем рассуждать логически. Если кому-то задали такую задачу, значит решение этой задачи есть. Наши математики ещё не доросли до того уровня, когда признаются своим ученикам в своем незнании чего-то. Разве что самые смелые. Остальные тупо повторяют то, чему учили когда-то их. Само собой напрашивается решение: составляем теоремы Пифагора для трех диагоналей граней, объединяем их в систему трех уравнений с тремя неизвестными, решаем и находим размеры прямоугольного параллелепипеда. Брррр! Ужас.
Теперь порассуждаем с другой стороны. Объем - это результат умножения трех измерений длины. У нас есть три длины диагоналей. Теоретически, из них можно получить объем. Давайте нарисуем наши диагонали прямоугольного параллелепипеда и посмотрим, что можно с ними сделать. Смотрим с разных сторон, чтоб понятнее было.
 |
| Диагонали граней прямоугольного параллелепипеда |
На картинке синим цветом выделены те элементы прямоугольного параллелепипеда, которые нам известны. Это диагонали граней. Красным цветом выделено то, что нам не известно. Это диагональ прямоугольного параллелепипеда и его линейные размеры (математики любят еще называть их измерениями параллелепипеда). Ну, и сам объем нам тоже не известен.
Теперь вооружимся древней теоремой дедушки Пифагора и запишем формулы размеров и диагоналей. Параллелепипед у нас прямоугольный, значит все углы между линейными размерами и гранями прямые. Не забываем также, что наша главная цель - найти объем.
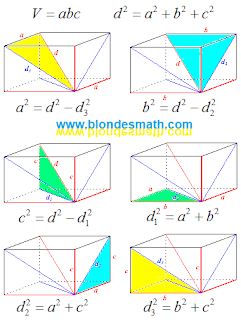 |
| Ребра и диагонали прямоугольного параллелепипеда |
Картинки несколько отвлекают от формул. Выписываем формулы отдельной кучкой. Математики в это случае с умным видом бы изрекли: "математическое множество формул". Смотрим на формулы и пытаемся хоть что-то соображать. Нам нужно избавиться от измерений и диагонали прямоугольного параллелепипеда, ведь они нам не известны. Вот если бы диагональ параллелепипеда выразить через диагонали боковых граней... Уж очень формулы в правой половине кучки похожи друг на друга.
 |
| Диагонали прямоугольного параллелепипеда формулы |
Есть! Квадраты диагоналей граней равны двум квадратам диагонали параллелепипеда. Теперь совсем просто. Как кубики в детском садике. Скобочки убираем, скобочки добавляем... И получаем формулу.
 |
| Диагонали прямоугольного параллелепипеда преобразования |
После этого полученную формулу подставляем в формулы с линейными размерами и получаем выражение линейных размеров через диагонали граней. Потом записываем формулу объема.
 |
| Диагонали прямоугольного параллелепипеда и объём |
Всё. Задача решена. Получилась очень красивая и изящная формула. Из суммы квадратов двух диагоналей граней вычитается квадрат третьей грани. Потом это перемножается, делится на восемь и получается квадрат объема прямоугольного параллелепипеда. Насколько понимаю я, это одно из основных свойств пространства. Используя принцип перегруппировки сомножителей и слагаемых, можно выводить подобные формулы для многомерных пространств с любым количеством измерений. Любой многомерный объем можно выразить через элементы с меньшим количеством измерений. К сожалению, нам математики об этом ничего не рассказывают. То ли сами ничего не знают, то ли стесняются. А ведь перед нами красота математики в первозданном виде, лишенная всяких заморочек, которые так любят наши учителя.
В условие не уточняется, что три диагонали - это диагонали граней. Есть же ещё четвёртая диагональ. А формула, действительно, получилась красивая.
ОтветитьУдалитьПодмечено правильно. Не научились мы ещё грамотно излагать свои мысли. Есть у математиков такое скользкое понятие "по умолчанию предполагается, что...", которое каждый может трактовать, как душе угодно. По умолчанию предполагается, что задача должна решаться теми математическими инструментами, которые изучаются в данный момент. Ученики, просящие в Интернете решить за них задачу, такими мелочами не заморачиваются)))
Удалить