Тема занятий:
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В ПРЯМОУГОЛЬНИКЕ
Тема предыдущего урока
Угловая симметрия в прямоугольнике
Урок 3
Три основных типа тригонометрических функций
Тригонометрические функции – это зависимости между углами и числами в прямоугольнике, выраженные в собственных единицах измерения. Собственная единица измерения – это одна из характеристик объекта, принятая в качестве единицы измерения.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В ПРЯМОУГОЛЬНИКЕ
Тема предыдущего урока
Угловая симметрия в прямоугольнике
Урок 3
Три основных типа тригонометрических функций
В прямоугольнике можно выделить три основных типа тригонометрических функций:
- бесконечные тригонометрические функции – тангенс и котангенс, геометрически это:
а) размер одной из сторон прямоугольника при единичном значении длины другой стороны, отражают связь чисел и единиц измерения;
б) размеры сторон прямоугольника при единичной площади, отражают законы умножения;
- конечные тригонометрические функции – синус и косинус, геометрически это размеры сторон прямоугольника при единичной диагонали, отражают проективные свойства пространства;
- линейные угловые функции – линейный синус (lin) и линейный косинус (los), геометрически это размеры сторон прямоугольника при единичном полупериметре, отражают законы сложения.
Другие типы тригонометрических функций в данной работе не рассматриваются, поскольку они не привлекли столь пристального внимания автора. Все тригонометрические функции устанавливают определенную связь между углами и числами. Вполне возможно, что математика некоторых внеземных цивилизаций может быть построена на углах точно так же, как у нас она построена на числах.
Выражение основных тригонометрических функций через стороны прямоугольника.
 |
| Выражение основных тригонометрических функций через стороны прямоугольника |
Основные соотношения по типам тригонометрических функций.
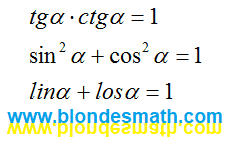 |
| Основные соотношения по типам тригонометрических функций |
Значения тригонометрических функций некоторых углов.
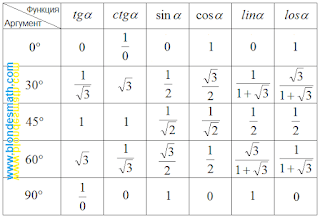 |
| Значения тригонометрических функций некоторых углов |
Выражение одних тригонометрических функций через другие.
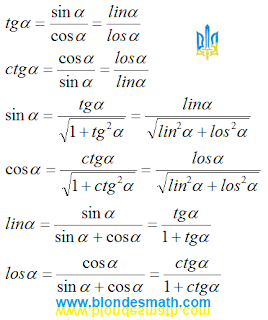 |
| Выражение одних тригонометрических функций через другие |
Пояснение для посетителей этого сайта. Если посмотреть на формулы тангенса и котангенса (последняя картинка), то может показаться, что между синусом с косинусом и линосом с лосесом нет никакой разницы. Но не торопитесь с выводами. Если две дроби равны, это совсем не означает, что равны их числители и знаменатели. Рассмотрим пример. Две трети равны четырем шестым. Но два не равно четырем, три не равно шести.
Более детально основные тригонометрические функции рассмотрены ниже.
На следующем уроке мы рассмотрим
Конечные тригонометрические функции
Конечные тригонометрические функции
Здравствуйте!
ОтветитьУдалитьЕсть ли какие-нибудь универсальные формулы для нахождения радиусов вписанных и описанных окружностей вокруг/около правильных n-угольинков?
Или зависимости суммы радиусов от количества и величины сторон?
P.S. вокрув/в
УдалитьИ желательно без пи.
Здравствуйте! Есть. Но с тригонометрическими функциями. А в современной математике таких функций без пи не бывает. Весь вопрос в том, от какой печки плясать? Смотрим в справочник Стеля :) и задаем радиус описанной окружности... А дальше уже по формулам. Есть формулы и без пи, могу картинку отсканировать.
УдалитьБыла бы очень признательна!
УдалитьЭтот комментарий был удален автором.
УдалитьДлина стороны задана.
Удалить