Степени числа 2

Последовательные степени числа два

Последовательные степени числа два от 0 до 29 представлены на таблице выше. Начинается таблица степеней числа 2 с показателя степени ноль. Любое число в нулевой степени равняется единице. Поэтому два в степени 0 равняется 1. Любое число в первой степени равняется самому себе. Поэтому 2 в степени 1 равно 2.

Если кому-то мало этой таблицы, тогда можете посмотреть другую, где степени числа 2 представлены до 49-й степени.

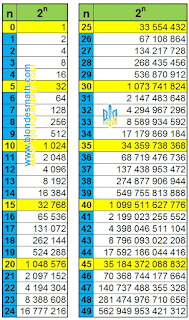Степени числа 2 от 0 до 49

Степени числа 2 от 50 до 69

Степени числа 2 от 70 до 89

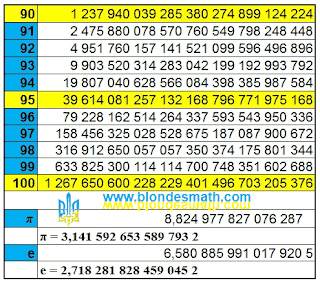Степени числа 2 от 90 до 100

Надеюсь, эти таблицы степеней числа 2 от 0 до 100 программистам понравятся. Математики любят совать всякую гадость куда попало. Как достойный ученик я не удержался, чтобы не всунуть в таблицу 2 в степени "пи" и 2 в степени "е". Авось, кому-нибудь из вундеркиндов это пригодится. А теперь маленький кусочек теории.

Два во второй степени означает, что число два нужно умножить само на себя. Поэтому 2 в степени 2 или 2 в квадрате равняется четырем.

2 х 2 = 4

Вообще, показатель степени показывает, сколько одинаковых чисел перемножается между собой. Так, два в третьей степени или 2 в кубе означает, что три числа 2 перемножаются между собой и это равняется восьми:

2 х 2 х 2 = 8

Два в четвертой степени будет произведением четырех двоек:

2 х 2 х 2 х 2 = 16

Эта таблица последовательных степеней числа два очень часто применяется в программировании, поскольку там используется двоичная система система счисления.

В заключение нужно ответить на вопрос вселенского масштаба: а 2 в бла-бла-бла степени на какую цифру заканчивается?

Два в любой степени заканчивается на одну из четырех цифр: 2, 4, 8, 6. Именно в такой последовательности они чередуются. (Евангелие от Меня: под выражением "любая степень" нужно понимать любое положительное целое число за исключением нуля. Аминь.) Искать формулы в Интернете мне откровенно лень. Беру карандаш и бумагу, рисую формулы - не правильно. Вторая попытка - то, что нужно. Несколько проверок - готово. Перед вами четыре формулы. Та формула, в которой при делении получается целое число, показывает, на какую цифру оканчивается два, возведенное в указанную степень.

Степени числа 2. Формулы для определения последней цифры.

На картинке приведены два примера использования формул. В первом случае 2 в степени 123456789 заканчивается на цифру 2. Во втором случае 2 в степени 11111 заканчивается на цифру 8.

Несколько ответов на вопросы в комментариях.

2 в 999 степени заканчивается на 88.

2 в 2000 и 2 в 2012 степенях заканчиваются на 6 (оба показателя степени без остатка делятся на 4).