Прежде, чем мы перейдем к формулировке определений тригонометрических функций с использованием портрета тангенса, нам нужно понять, чем тригонометрический круг отличается от всех остальных кругов. В своих рассуждениях мы будем использовать один математический фокус, смысл которого основан именно на этих отличиях.
Возьмем рисунок окружности из определения тригонометрических функций. Выглядит он вот так.
 |
| Обычная окружность |
На рисунке изображена обычная окружность произвольного радиуса. Поскольку в центре окружности нахально развалилась декартова система координат, то все точки этой окружности имеют вертикальные и горизонтальные координаты. Радиус окружности и координаты точек выражаются числами. Точки пересечения осей координат и окружности определяются величиной радиуса окружности и численно ему равны.
Для того, чтобы превратить обычную окружность в тригонометрическую, нужно все элементы окружности разделить на радиус окружности. Буквы "X" и "Y" являются ярлычками системы координат, обозначающими её навязчивое присутствие на нашем рисунке. Эти буквы на радиус не делятся, как и буква "В", обозначающая точку на окружности. Точка "0" (ноль) в результате деления на радиус так и останется точкой "0" (помните, ноль, деленный на любое число, равняется нулю?). Угол альфа можно разделить на число, но нельзя разделить на радиус окружности (кстати, вот вам готовое доказательство того, что деление не имеет смысла)))), поэтому угол лучше не трогать, во избежание крупных неприятностей (из всех присутствующих на картинке, угол - самый крутой элемент, он присутствует во всех тригонометрических функциях в своем естественном виде). У нас остаются только радиус окружности и координаты точки "В", которые мы можем разделить на величину радиуса окружности.
Понятно, что при делении радиуса окружности на точно такой же радиус, мы в результате получим единицу. А вот при делении координат точки окружности на радиус мы получим значения синуса и косинуса угла альфа (по определению тригонометрических функций). Вот как выглядят наши преобразования на картинке.
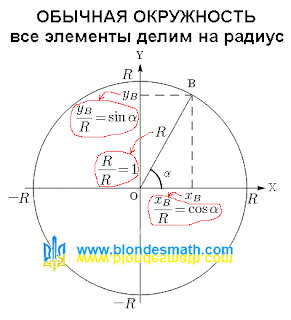 |
| Обычная окружность делим на радиус |
Теперь нам остается только заменить все радиусы на единички а координаты точки на синус и косинус угла альфа и у нас получится тригонометрическая окружность. Мы даже можем сформулировать определение единичной окружности (пусть вундеркинды учат):
окружность с радиусом, равным единице, называется тригонометрической окружностью, если в центре окружности находится центр декартовой системы координат.
Это определение далеко не полное и не учитывает целое море нюансов, на которые математики обычно не обращают внимания. Но об этом мы лучше поговорим при изучении свойств тригонометрических функций. А пока посмотрим на картинку, как выглядит тригонометрическая окружность во всей своей красе.
 |
| Тригонометрический круг |
Собственно, это и есть тригонометрический круг. Если на него поместить значения разных углов и соответствующие им значения синуса и косинуса, то мы получим тригонометрический круг синуса и косинуса.
Теперь о том фокусе, который мы будем проделывать во время формулирования определений тригонометрических функций. Здесь мы радиус окружности заменили на единицу, а там мы будем поступать наоборот - будем единицу заменять радиусом окружности. То есть, от тригонометрической окружности переходить к окружности произвольного радиуса, как того требует учебник по математике.
не знаю что в школе делала,я обсалютно тупая,сейчас очень стыдно,чистый лист(можно ли наверстать школьную рограмму?
ОтветитьУдалитьПри желании можно вызубрить всё. Что касается тупости, то это всё относительно. Лично я сейчас затрудняюсь сказать, кто тупее - я или писатели учебников по математике. В тригонометрии я только сейчас начинаю кое-что понимать. При решении задач мне уже проще самому, по ходу дела, вывести нужную тригонометрическую функцию, чем разбираться с учебниками или справочниками в поиске нужного соотношения. Дерзайте, и у вас всё получится.
Удалить