Начинаем рассуждать. Параллелепипед и ромб в основании - это такая коробочка, которая сверху похожа на ромб. У такого параллелепипеда действительно можно нарисовать две пары диагоналей, длины которых будут разными. Из нижней вершины с острым углом в верхнюю вершину с острым углом можно провести длинную диагональ. А вот тупые вершины (не в смысле, что эти вершины ничего не понимают, а в смысле, что эти вершины прихватизировали тупые углы) будут соединяться короткими диагоналями. Таких диагоналей две, их длина одинаковая. Посмотрим на картинке, как выглядит одна из таких диагоналей.
 |
| Диагональ, параллелепипед и ромб |
Диагональ прямоугольного параллелепипеда показана красным цветом, диагонали ромба основания показаны синим цветом. Если очень сильно постараться, напрячь свое воображение и внимательно присмотреться к верхней картинке, то можно увидеть прямоугольный треугольник. Параллелепипед у нас прямоугольный. Значит, боковое ребро расположено под прямым углом к основанию. Диагональ основания (синенькая), диагональ параллелепипеда (красненькая) и ребро (черненькое, мелированое, не успело в парикмахерской перекраситься) образуют этот прямоугольный треугольник. А там, где есть прямоугольный треугольник, там царствует теорема древнего Пифагора. Всегда, не зависимо от того, кого вы в своей стране избрали царём или президентом.
В низу, под картинкой, записана эта самая знаменитая теорема применительно к нашему случаю. Не удивляйтесь, если в таком виде вы встречаете теорему Пифагора впервые. Во-первых, не все учились с вами в одном классе и они могут не знать, как именно вас учили правильно записывать теорему Пифагора. Во-вторых, в теореме Пифагора главным является не принятая кем-то система закорючек, а смысл - берем две перпендикулярных штучки, возводим в квадрат, складываем в кучку и получаем третью штучку в квадрате. У нас квадрат ребра и квадрат диагонали ромба чудненько складываются в квадрат диагонали параллелепипеда.
Теперь нам необходимо разобраться с диагональю ромба. Берем нашу коробочку в форме прямоугольного параллелепипеда, открываем крышечку и заглядываем внутрь. Почему мы заглядываем внутрь коробочки а не изучаем саму крышечку? Безотказно работает теорема любопытной обезьяны. Попробуйте что-нибудь отрыть и не заглянуть внутрь. А зачем тогда открывали?! Любой, даже безграмотный, математик вам скажет, что теорема требует доказательства. Один момент. Попросите свою маму купить вам что-то в коробочке. Когда она вам её принесет, вы, с закрытыми глазами, откройте крышечку коробочки, а саму коробочку, не глядя, выбросьте в мусор. Не получилось? Всё, теорема доказана.
И так, мы остановились на том, что, встав в позу теоремы Пифагора, мы заглядываем внутрь коробочки. Что мы там видим? Если вы верили в Конец Света 2012, тогда там спрятаны припасы на всю оставшуюся жизнь. Вынимайте их из коробки и можете смело доедать (вы ещё долго будете извлекать свои припасы из самых неожиданных мест). Пока вы не придумаете следующую дату Конца Света, вам ничто не угрожает. С пророчеством советую поторопиться. Вокруг очень много жаждущих славы пророков, а ещё больше желающих впихнуть вам партию залежалого товара. Если же вы не верите в Конец Света, то в коробочке были новогодние сладости, которые уже закончились.
Всё, наша коробочка пустая и мы можем внимательно изучить донышко. Оно имеет форму ромба, у которого можно провести диагонали. При пересечении, эти диагонали образуют чудненькие треугольнички. Аж четыре штуки. Мы люди не жадные, нам достаточно одного. Что мы знаем об этом треугольничке, который на картинке ниже он закрашен в чудный цвет? Этот треугольник точно не Бермудский и не любовный. А какой? Лезем в Интернет и ищем свойства ромба. Мы их когда-то учили в школе, но это было так давно... В Интернете полно всякой ерунды, но есть и кое-то интересное нам. Все стороны ромба одинаковые. Диагонали ромба разные. Пересекаются диагонали под прямым углом. Точка пересечения диагоналей делит их на две равные половинки. Каждая диагональ делит угол в вершине поровну (у ромбов и квадратов диагонали не жадные). Кажется, всё. Прочая ерунда о ромбах нас не интересует.
И так, в результате наших научных исследований мы установили, что наш треугольник является прямоугольным. Гипотенуза у него равна длине стороны ромба, катеты равняются половинкам диагоналей. Снова примеряем деда Пифагора. Длину гипотенузы мы знаем, а вот с двумя катетами проблема. Какой-то лентяй не потрудился измерить диагонали. Зато это чудо умудрилось вымерить величину угла в одной вершине. В традиционном виде теорема Пифагора не катит (это не опечатка, это в смысле "не подходит"). Остается только тригонометрия. Она тоже работает в прямоугольных треугольниках, но придумали её математики исключительно для того, чтобы издеваться над детьми. Лично мне так кажется. Думаю, эта идея соберет не маленькую группу Вконтакте. "Я ненавижу тригонометрию" - красивое название для группы, дарю.
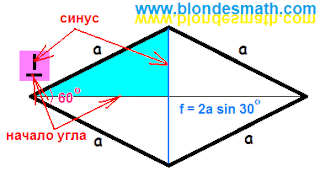
Как сказали бы врачи, показаниями к применению тригонометрии является невозможность применения теоремы Пифагора из-за отсутствия двух размеров треугольника и наличие значения одного из углов. Если бы у нас не было угла, тогда и медицина была бы бессильна. Как применить тригонометрию? Не будем рыскать по Интернету, я покажу вам более надежный инструмент. Назвал я его "портрет тангенса". Приставляем его к вершине треугольника, значение угла в которой нам известно. Горизонтальную палочку располагаем параллельно линии, от которой мы отсчитываем угол (у нас это горизонтальная диагональ). Потом вспоминаем "тангенс - это синус на косинус". Верхняя палочка портрета обозначает синусы, нижняя палочка - косинусы. Нам нужно найти вертикальный катет треугольника. Значит, для этого гипотенузу нужно умножить на синус угла. Если бы нам нужен был горизонтальный катет, мы бы умножали на косинус этого же угла. Полная длина вертикальной диагонали ромба (синенькая) получается равной двум длинам катета треугольника.
 |
| Диагональ, параллелепипед и ромб |
Всё. С задачей мы разобрались. Обозначаем диагональ ромба буквой "f", сторону - буквой "а", угол - буквой "альфа". Диагональ параллелепипеда мы обозначим буквой "d", а его высоту - буквой "h". Теперь записываем формулы для решения, подставляем в них известные нам значения и получаем результат.
 |
| Диагональ, параллелепипед и ромб |
Длина меньшей диагонали получилась равной 10 сантиметров. Можно, конечно, вычислить и длину большей диагонали, но теорема любопытной обезьяны в этом случае наотрез отказывается работать. Она (теорема) точно знает, что ничего вкусненького или интересного в результате вычислений мы не получим.
Комментариев нет:
Отправить комментарий